Практикум по элементарной математике (цвет)

2) Вторая часть задания состоит из различных задач на составление уравнений. Некоторые из них опираются на формулу сложного процента. В простейшей схеме речь идет о начислении процентов на предоставленную в распоряжение банка, компании или частному лицу сумму денег из условия % за определенный период времени (например, месяц, квартал, год и т.д.). Это означает, что размер вклада за обозначенный период времени будет увеличиваться в раз. Если размер вклада через таких периодов обозначить через , то по данной схеме будем иметь:

, , … , .

Пример 1. Два бизнесмена внесли для общей торговли по 48 тыс. руб.: первый – на 1 год, а второй – на 2 года. Как они должны поделить между собой через два года 42 тыс. руб. полученной прибыли?

Решение. Условие задачи подразумевает, что процент прибыли за каждый год был одинаковым и что после первого года совместной работы первый бизнесмен получил назад лишь свой первоначальный вклад 48 тыс. руб. Это замечание позволяет вычислить прибыль каждого бизнесмена. А именно: - прибыль первого бизнесмена за первый год, - прибыль первого бизнесмена за два года, - прибыль второго бизнесмена за два года. Отсюда получаем уравнение:

Условию задачи удовлетворяет , поэтому (тыс. руб.) – итоговая прибыль первого бизнесмена и (тыс. руб.) – итоговая прибыль второго бизнесмена. #

Решить задачи:

15) Два велосипедиста выехали одновременно из одного пункта в одном направлении. Первый из них ехал со скоростью 15км/ч, а второй – со скоростью 12км/ч. Спустя полчаса из того же пункта в том же направлении выехал третий велосипедист, который через некоторое время догнал второго, а еще через 1 час 30 мин догнал и первого. Найдите скорость третьего велосипедиста.

16) Два человека вышли одновременно: один – из пункта А в пункт В, другой – из В в А. Каждый шел с постоянной скоростью и, придя в конечный пункт, сразу же отправлялся обратно. Первый раз они встретились в 12км от В, второй раз – через 6 ч после первой встречи в 6км от А. Найдите расстояние между пунктами А и В и скорости пешеходов.

17) Предприятие взяло кредит в банке на 3 года под 20% годовых. Какую часть кредита предприятию необходимо выплатить банку по истечении первого года, чтобы по истечении третьего года оставалось выплатить менее 80% взятого кредита?

18) Предприятие взяло в банке кредит на 3 года под 25% годовых. Какую часть кредита предприятию необходимо выплатить банку по истечении второго года, чтобы по истечении третьего года оставалось выплатить менее 75% взятого кредита?

19) Два компаньона вложили деньги в общее дело. Первый внес 40 тыс. руб., а второй – 60 тыс. руб. Через месяц первый забрал свои деньги (без дохода), а еще через месяц они решили поделить доход в размере 17 тыс. руб., полученный за эти два месяца. Как они должны поделить между собой доход?

19 задание

1) В первой части задания содержатся различные задачи на решение неравенств.

Пример 1. Решить неравенство: .

Решение. Прологарифмируем заданное неравенство по основанию 2:

Решить неравенства:

1) ; 2) ; 3) ; 4) ; 5) ; 6) ; 7) ;

8) ; 9) ; 10) ;

11) ; 12) ; 13) ; 14).

2) Во второй части задания приведены задачи по планиметрии.

Пример 2. В выпуклом четырехугольнике длины диагоналей и равны и . Точки являются соответственно серединами сторон . Площадь равна . Найдите длины диагоналей и четырехугольника .

Решение. Выполним чертеж:

Так как и являются средними линиями треугольников и , имеющих общее основание , то и . Аналогично и . Следовательно, - параллелограмм. Пусть - величина . Для определенности будем считать, что . Тогда , поэтому , и . Применяя теперь теорему косинусов к , получим , т.е.

.

Аналогичным образом, учитывая, что , получим:

. #

Решить задачи:

15) В прямоугольном треугольнике угол прямой, , а радиус описанной окружности равен . Найдите расстояние от вершины до точки касания вписанной окружности с катетом .

16) В треугольнике площадью и проведена окружность радиуса с центром, лежащим на ВС, которая касается сторон и . Найдите длины сторон треугольника .

17) В квадрат со стороной равной вписана окружность, которая касается в точке . Найти длину хорды, соединяющей точки, в которых окружность пересекается с прямой .

18) В равнобедренный треугольник с углом при основании вписан квадрат так, что одна из его сторон лежит на основании треугольника. Найти значение , при котором площадь квадрата будет составлять площади треугольника.

19) В выпуклом четырехугольнике точки и являются соответственно серединами сторон и , а - точка пересечения отрезков и . Известно, что , а . Найдите длины диагоналей и четырехугольника , если площадь четырехугольника равна .

20 задание

1) В первой части задания содержатся различные задачи на решение неравенств.

Пример 1. Решить неравенство: .

Решение. Решение неравенства сводится к решению совокупности двух систем неравенств:

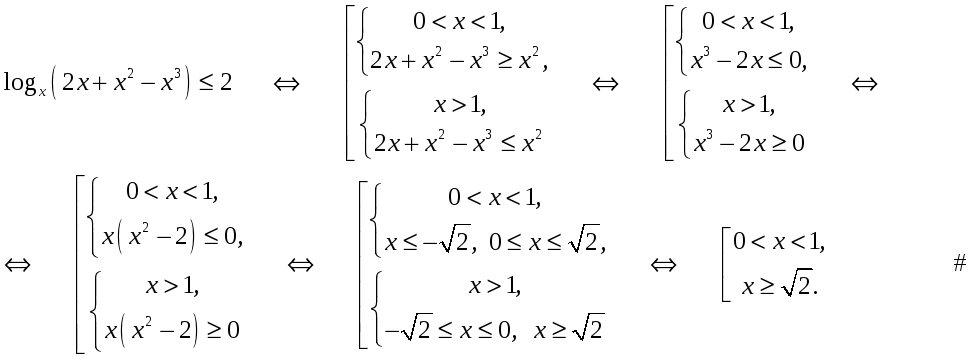
Решить неравенства:

1) ; 2) ; 3) ;

4) ; 5) ; 6) ; 7) ;

8) ; 9) ; 10) ;

11) ; 12) ; 13) .

2) Вторая часть задания содержит различные задачи на составление уравнений.

Пример 2. Если в условиях длительного финансового кризиса курс рубля по отношению к доллару падает на % в год, то, что выгоднее: а) сделать валютный вклад на 4 года с начислением 60% или б) конвертировать доллары в рубли и сделать рублевый вклад на 4 года с начислением 510%?

Решение. Прежде всего, уточним: курс доллара – это стоимость в рублях одного доллара, а курс рубля – это стоимость в долларах одного рубля. Следовательно, если - курс рубля, то - курс доллара. Предположим, что речь идет о начальной сумме вклада рублей. После конвертации этой суммы денег будет долларов. По условию задачи через 4 года сумма валютного вклада составит долларов, а сумма рублевого вклада составит рублей. Через 4 года курс рубля станет равным , поэтому конвертация рублевого вклада составит долларов. Поскольку , то выгоднее сделать валютный вклад. #

Решить задачи:

14) Сумма членов бесконечно убывающей геометрической прогрессии равна наибольшему значению функции на отрезке , а разность между первым и вторым членами прогрессии равна . Найдите знаменатель прогрессии.

15) На сколько процентов должна убывать ежеквартальная выплата за аренду оборудования в течение года, чтобы средняя выплата за второе полугодие на 19% была бы меньше средней выплаты за первое полугодие?

16) На сколько процентов должна возрастать заработная плата за квартал в течение года, чтобы средняя заработная плата за второе полугодие на 21% превысила среднюю заработную плату за первое полугодие?

17) В условиях нестабильности рынка закупочная цена тонны пшеницы в течение первого месяца повысилась на 10%, течение второго снизилась на 30%, а в течение третьего повысилась на 20%. На сколько процентов снизилась или повысилась закупочная цена тонны пшеницы за три месяца по отношению к начальной цене?

18) Вследствие нестабильности финансового рынка курс рубля по отношению к доллару в течение первого месяца снизился на 10%, в течение второго повысился на 30%, а в течение третьего снизился на 20%. На сколько процентов снизился или повысился курс рубля за три месяца по отношению к начальному курсу?

19) Курс доллара по отношению к рублю ежегодно растет на 25%. Выгодно ли вкладчику сделать рублевый вклад в банк на 3 года с начислением 94% от суммы вклада по сравнению с конвертацией в доллары?

21 задание

1) В первой части задания содержатся различные задачи на решение уравнений.

Пример 1. Решить уравнение: .

Решение. Имеем:

Решим по отдельности неравенство:

и уравнение, образующие систему:

Таким образом,

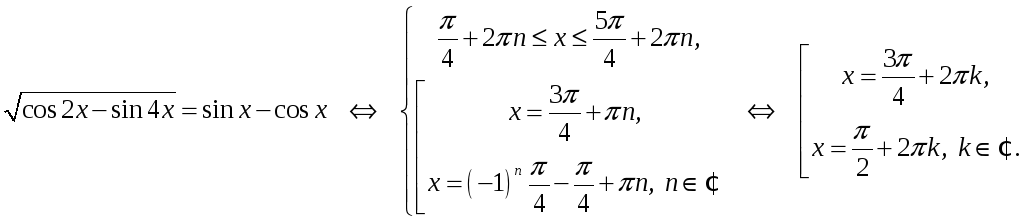
Решить уравнения:

1) ; 2) ; 3) ;

4) ; 5) ; 6) ;

7) ; 8) ; 9) ;

10) ; 11) ;

12) ; 13) .

2) Во второй части задания приведены задачи по стереометрии.

Пример 2. В основании четырехугольной пирамиды лежит прямоугольник, площадь которого равна . Боковые ребра пирамиды равны и образуют с плоскостью основания угол в . Угол между диагоналями основания равен . Найдите объем пирамиды.

Решение. Выполним чертеж:

Так как боковые ребра пирамиды равные, то ее высота проектируется в центр основания. Пусть и . Поскольку , то , , и . Следовательно, и . Но , поэтому

. #

Решить задачи:

14) В параллелепипеде длины трех ребер, выходящих из общей вершины, равны , и , ребра и взаимно перпендикулярны, а ребро образует с каждым из них угол . Найдите объем параллелепипеда.

15) Объем конуса равен . Найдите объем правильной четырехугольной пирамиды, вписанной в конус.

16) Объем конуса равен . Найдите объем правильной четырехугольной пирамиды, описанной около этого конуса.

17) Отношение полной поверхности конуса к поверхности вписанного в него шара равно . Найти угол между высотой и образующей конуса и допустимые значения .

18) Основание пирамиды – прямоугольный треугольник с катетами 6см и 8см. Каждое боковое ребро пирамиды имеет длину, равную 13см. Найти площадь боковой поверхности пирамиды.

19) Основание пирамиды – прямоугольный треугольник с катетами 3см и 4см. Каждая боковая грань наклонена к плоскости основания под углом в . Найдите площадь полной поверхности пирамиды.

20) Основанием пирамиды служит равносторонний треугольник со стороной, равной . Одна из боковых граней пирамиды – также равносторонний треугольник, причем эта грань перпендикулярна плоскости основания. Вычислите площадь полной поверхности пирамиды.

22 задание

1) Первая часть задания предполагает решение различных уравнений.

Пример 1. Решить уравнение: .

Решение. Так как и , то . Функция возрастает на интервале , поэтому имеем:

Пример 2. Решить уравнение: .

Решение. Решение заданного уравнения сводится к решению системы:

Решить уравнения и системы уравнений:

1) 2) 3) 4)

5) 6) 7)

8) ; 9) ;

10) ; 11) ; 12) ;