
Практикум по элементарной математике (цвет)
.doc
![]()
Выделив
на оси синусов красным цветом отрезок
![]() ,
получим определяемую этим отрезком
дугу единичной окружности
,
получим определяемую этим отрезком
дугу единичной окружности
![]() ,
закрашенную синим цветом. Следовательно,
решая неравенство
,
закрашенную синим цветом. Следовательно,
решая неравенство
![]() ,
получим ответ:
,
получим ответ:
![]() .
#
.
#
Решить неравенства:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() ;
6)
;
6)
![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
9)
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
![]() ;
12)
;
12)
![]() ;
13)
;
13)
![]() ;
14)
;
14)
![]() ;
15)
;
15)
![]() ;
;
16)
![]() ;
17)
;
17)
![]() ;
18)
;
18)
![]() .
.
2) Вторая часть задания содержит задачи по планиметрии.
Пример 2. В окружность радиуса 17см вписан четырехугольник, диагонали которого взаимно перпендикулярны и находятся на расстоянии 8см и 9см от центра окружности. Найдите площадь четырехугольника.
Решение. Выполним чертеж:






![]()




![]()
![]()

![]()
![]()


![]()
![]()
![]()
Здесь
![]() см
и
см
и
![]() см,
поэтому
см,
поэтому
![]() см
и
см
и
![]() см.
Нетрудно понять, что
см.
Нетрудно понять, что
![]() см
и
см
и
![]() см.
Так как
см.
Так как
![]() ,
то
,
то
![]() #
#
Решить задачи:
19)
В окружность радиуса 10см
вписан четырехугольник, диагонали
которого взаимно перпендикулярны. Длины
диагоналей равны 12см
и
![]() см.
Найдите длины сторон четырехугольника.
см.
Найдите длины сторон четырехугольника.
20)
Через концы дуги окружности радиуса
![]() ,
содержащей
,
содержащей
![]() ,
проведены касательные. Найти площадь
фигуры, образованной касательными и
взятой дугой окружности.
,
проведены касательные. Найти площадь
фигуры, образованной касательными и
взятой дугой окружности.
14 задание
1) При решении систем тригонометрических уравнений возникает особенность, которую поясним на конкретном примере.
Пример
1. Решить
систему уравнений:

Решение. Имеем:

Замечание.
Наличие в ответе двух параметров
![]() и
и
![]() является обязательным условием, ибо
при
является обязательным условием, ибо
при
![]() мы будем иметь только малую часть решений
исходной системы уравнений:
мы будем иметь только малую часть решений
исходной системы уравнений:
![]() ,
,
что, разумеется, означает потерю большей части решений. В этом и заключается упомянутая выше особенность при решении тригонометрических систем.
Решить системы уравнений:
1)
![]() 2)
2)
 3)
3)
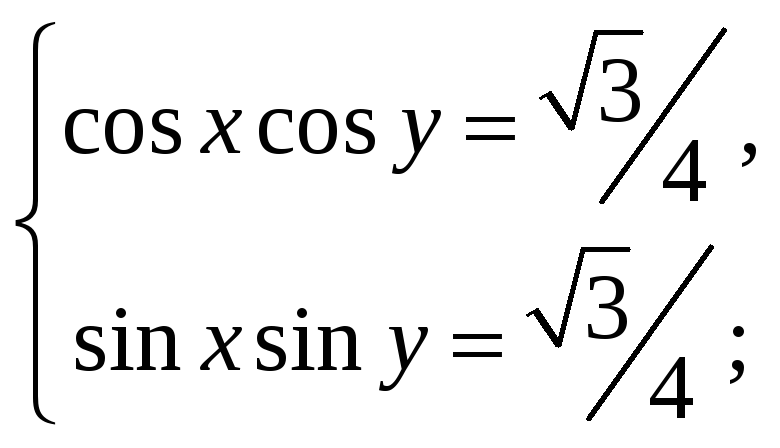 4)
4)
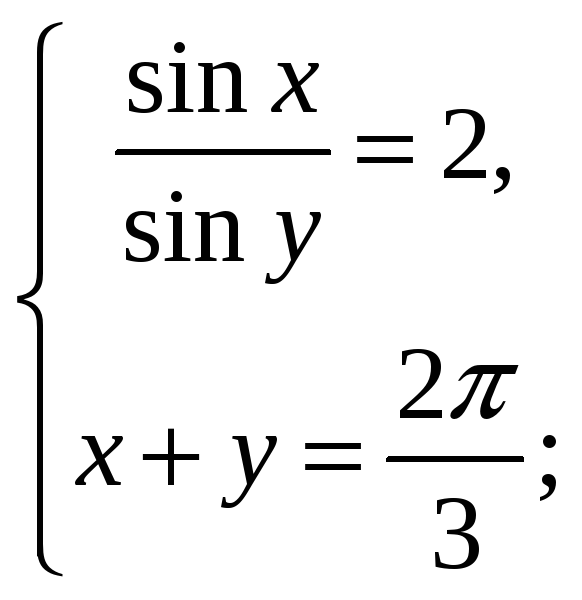
5)
 6)
6)
 7)
7)
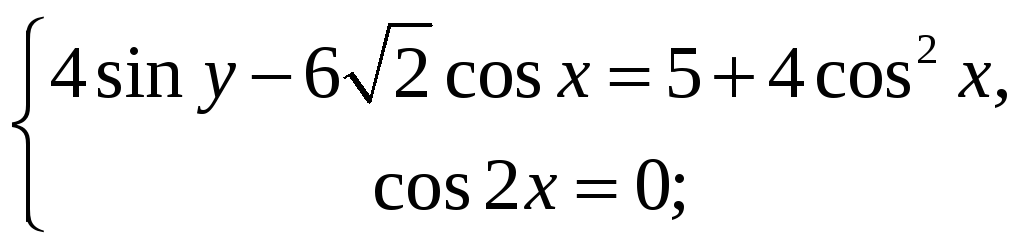
8)
 9)
9)
 10)
10)
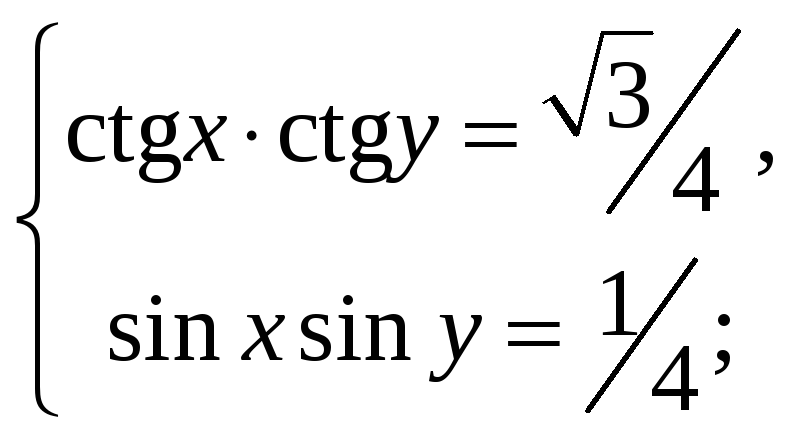
11)
 12)
12)
 13)
13)
![]()
2) Во второй части задания содержатся различные задачи на прогрессии.
Решить задачи:
14) Сумма первых десяти членов арифметической прогрессии равна 155, а сумма первых двух членов геометрической прогрессии равна 9. Определите эти прогрессии, если первый член арифметической прогрессии равен знаменателю геометрической прогрессии, а первый член геометрической прогрессии равен разности арифметической прогрессии.
15) Первый член некоторой бесконечно убывающей геометрической прогрессии равен 2, а ее сумма равна 5. Найдите сумму квадратов членов исходной прогрессии.
16) Найдите сумму бесконечно убывающей геометрической прогрессии, если сумма всех ее членов, стоящих на нечетных местах, в 4 раза больше суммы всех ее членов, стоящих на четных местах, и сумма первых трех прогрессии равна 63.
17)
Сумма бесконечно убывающей геометрической
прогрессии равна 3,5,
а сумма квадратов членов этой же
прогрессии равна
![]() .
Найдите сумму кубов членов этой
прогрессии.
.
Найдите сумму кубов членов этой
прогрессии.
18)
Найдите сумму бесконечно убывающей
геометрической прогрессии, третий член
которой, утроенное произведение первого
члена на четвертый и второй член образуют
в указанном порядке арифметическую
прогрессию с разностью, равной
![]() .
.
19) Сумма бесконечно убывающей геометрической прогрессии равна 243, а сумма ее первых пяти членов равна 275. Найдите прогрессию.
20)
Сумма второго и восьмого членов бесконечно
убывающей геометрической прогрессии
равна
![]() ,
а сумма второго и шестого членов,
уменьшенная на
,
а сумма второго и шестого членов,
уменьшенная на
![]() ,
равна четвертому члену этой прогрессии.
Найдите сумму квадратов членов этой
прогрессии.
,
равна четвертому члену этой прогрессии.
Найдите сумму квадратов членов этой
прогрессии.
15 задание
1) Первая часть задания посвящена решению различных алгебраических уравнений.
Решить уравнения:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
;
4)
![]() ;
5)
;
5)
![]() ;
6)
;
6)![]() ;
;
7)
![]() ;
8)
;
8)
![]() ;
9)
;
9)
![]() ;
;
10)
![]() ;
11)
;
11)
![]() ;
;
12)
![]() ;
13)
;
13)
![]() ;
;
14)
![]() ;
15)
;
15)
![]() ;
16)
;
16)
![]() .
.
2) Вторая часть задания предназначена для решения задач по планиметрии.
Пример
1. Даны
треугольник
![]() с тупым углом при вершине
с тупым углом при вершине
![]() и ромб
и ромб
![]() ,
все вершины которого лежат на сторонах
треугольника
,
все вершины которого лежат на сторонах
треугольника
![]() .
Найти площадь треугольника
.
Найти площадь треугольника
![]() ,
если длина отрезка
,
если длина отрезка
![]() равна 0,02м,
длина отрезка
равна 0,02м,
длина отрезка
![]() равна 7см, а
радиус окружности, вписанной в ромб,
равен 1см.
равна 7см, а
радиус окружности, вписанной в ромб,
равен 1см.
Решение. Сделаем чертеж:


![]()
![]()





![]()
![]()






![]()

![]()
![]()
![]()
![]()
![]()
Так
как
![]() - ромб, то
- ромб, то
![]() и, значит,
и, значит,
![]() .
Отсюда следует, что
.
Отсюда следует, что
![]() .
Обозначим
.
Обозначим
![]() и
и
![]() .
Тогда имеем:
.
Тогда имеем:
![]() ,
откуда
,
откуда
![]() и
и
![]() .
Пусть
.
Пусть
![]() - высота
- высота
![]() и
и
![]() .
Тогда
.
Тогда
![]() см,
где
см,
где
![]() - диаметр вписанной в ромб окружности.
По теореме косинусов, примененной к
- диаметр вписанной в ромб окружности.
По теореме косинусов, примененной к
![]() ,
,
![]() .
Поскольку
.
Поскольку
![]() ,
а по условию задачи угол
,
а по условию задачи угол
![]() является острым, то
является острым, то
![]() .
Следовательно,
.
Следовательно,

Теперь
находим
![]() ,
,
![]() и
и
![]() .
#
.
#
Решить задачи:
17)
В квадрат вписан другой квадрат. Один
из острых углов между сторонами квадратов
равен
![]() .
При каком значении
.
При каком значении
![]() площадь вписанного квадрата составляет
площадь вписанного квадрата составляет
![]() площади описанного?
площади описанного?
18)
На продолжении стороны
![]() ромба
ромба
![]() за точку
за точку
![]() взята точка
взята точка
![]() так, что угол
так, что угол
![]() - тупой. Отрезки
- тупой. Отрезки
![]() и
и
![]() пересекаются в точке
пересекаются в точке
![]() .
Найти площадь треугольника
.
Найти площадь треугольника
![]() ,
если длина отрезка
,
если длина отрезка
![]() равна 0,3дм,
длина отрезка
равна 0,3дм,
длина отрезка
![]() равна 4см, а
высота ромба равна 2см.
равна 4см, а
высота ромба равна 2см.
19) Около окружности радиуса R описан параллелограмм. Площадь четырехугольника с вершинами в точках касания окружности и параллелограмма равна S. Найти длины сторон параллелограмма.
20) Рассматриваются всевозможные трапеции, вписанные в окружность радиуса R, такие, что одно из оснований является диаметром этой окружности. Найдите углы той из этих трапеций, которая имеет наибольшую площадь.
16 задание
1) Первая часть задания посвящена решению различных уравнений.
Решить уравнения:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
;
8)
![]() ;
9)
;
9)
![]() ;
10)
;
10)
![]() ;
;
11)
![]() 12)
12)
![]()
13)
![]() ;
14)
;
14)
![]() .
.
2) Во второй части задания содержатся различные задачи на составление уравнений.
Решить задачи:
15) Два куска одинаковой ткани стоят вместе 9100 руб. Когда из первого куска продали столько, сколько было первоначально во втором, а из второго – половину того, что было первоначально в первом, остаток первого куска оказался на 10м больше остатка второго куска. Сколько метров ткани было в каждом куске, если 1м ткани стоит 140 руб.?
16) В ателье поступило по одному куску черной, зеленой и синей ткани. Хотя зеленой ткани было на 9м меньше, чем черной, и на 6м больше, чем синей, стоимость кусков была одинаковой. Известно также, что стоимость 4,5м черной ткани равна общей стоимости 3м зеленой и 0,5м синей ткани. Сколько метров было в каждом куске?
17) На сколько процентов сократится время в пути, если на одной четверти пути предполагаемую скорость увеличить на одну треть, а на оставшейся части пути предполагаемую скорость увеличить на одну четверть?
18) На сколько процентов увеличится время в пути, если на одной четверти пути предполагаемую скорость уменьшить на одну четверть, а на оставшейся части пути предполагаемую скорость уменьшить на одну треть?
19) После проведенной реконструкции производительность труда на предприятии в течение первого года работы повысилась на 20%. В течение второго года она снизилась на 30%, а в течение третьего года работы вновь повысилась на 10%. На сколько процентов снизилась или повысилась производительность труда за три года по отношению к производительности труда на предприятии до реконструкции?
20)
Разность между вторым и шестым членами
бесконечно убывающей геометрической
прогрессии равна
![]() ,
а разность между четвертым и восьмым
членами равна
,
а разность между четвертым и восьмым
членами равна
![]() .
Найдите отношение суммы квадратов
членов этой прогрессии к сумме кубов
членов этой прогрессии.
.
Найдите отношение суммы квадратов
членов этой прогрессии к сумме кубов
членов этой прогрессии.
17 задание
1) Первая часть задания содержит различные задачи на неравенства.
Решить неравенства:
1)
![]() 2)
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
;
5)
![]() ;
6)
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
 ;
11)
;
11)
![]() ;
;
12)
![]() ;
13)
;
13)
![]() ;
14)
;
14)
![]() ;
;
15)
![]() ;
16)
;
16)
![]() .
.
2) Вторая часть задания посвящена решению задач по планиметрии.
Пример
1. В окружность
радиуса
![]() вписан равнобедренный треугольник.
Какую наибольшую площадь может иметь
этот треугольник?
вписан равнобедренный треугольник.
Какую наибольшую площадь может иметь
этот треугольник?
Решение. Выполним чертеж:

![]()






![]()


![]()

![]()



![]()
![]()
![]()
Пусть
![]() - величина
- величина
![]() .
Очевидно,
.
Очевидно,
![]() может меняться в пределах от
может меняться в пределах от
![]() до
до
![]() .
Так как
.
Так как
![]() ,
то
,
то
![]() .
Следовательно,
.
Следовательно,
![]() и
и
![]() .
.
![]()
Таким
образом,
![]() .
Чтоба найти наибольшее значение для
.
Чтоба найти наибольшее значение для
![]() ,
продифференцируем
,
продифференцируем
![]() по
по
![]() и решим уравнение
и решим уравнение
![]() :
:


Учитывая
ограничение
![]() ,
получаем единственную точку
,
получаем единственную точку
![]() .
Знаки функции
.
Знаки функции
![]() на
на
![]()
![]()
![]()





 0
0
![]()
![]()
показывают,
что наибольшую площадь равнобедренный
треугольник
![]() будет иметь при
будет иметь при
![]() :
:
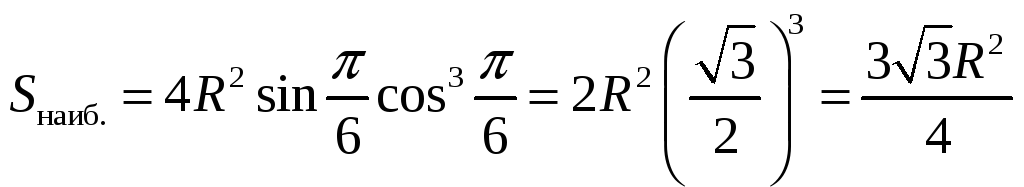 .
#
.
#
Решить задачи:
17)
В окружность радиуса
![]() вписан прямоугольный треугольник. Какую
наибольшую площадь может иметь этот
треугольник?
вписан прямоугольный треугольник. Какую
наибольшую площадь может иметь этот
треугольник?
18)
Равнобедренные треугольники равной
площади
![]() вписаны в окружность. Какой наименьший
радиус может иметь эта окружность?
вписаны в окружность. Какой наименьший
радиус может иметь эта окружность?
19)
Прямоугольные треугольники равной
площади
![]() вписаны в окружность. Какой наименьший
радиус может иметь эта окружность?
вписаны в окружность. Какой наименьший
радиус может иметь эта окружность?
20) Рассматриваются всевозможные трапеции, обе боковые стороны и меньшее основание которых равны а. Найдите большее основание той из трапеций, которая имеет наибольшую площадь.
18 задание
1) Первая часть задания предполагает решение различных уравнений.
Решить уравнения:
1)
![]() ;
2)
;
2)
![]() ;
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() ;
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() ;
;
9)
![]() ;
10)
;
10)
![]() ;
11)
;
11)
![]() ;
;
12)
![]() ;
13)
;
13)
![]() ;
14)
;
14)
![]() .
.
