Практикум по элементарной математике (цвет)
.doc 
,
,
,
,
,
,
,
,
(указанных
формул приведения достаточно для решения
задач, так как наименьший
период у функций
и
равен
,
а
у функций
и
он равен
),
формул
для решения простейших тригонометрических
уравнений:
,
,
,
и таблицы значений основных тригонометрических функций для некоторых важнейших значений аргумента:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
Решить уравнения:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
.
2) Вторая часть задания содержит задачи по планиметрии, решения которых основаны на использовании тригонометрии.
Пример
1.
Основание
равнобедренного треугольника
является хордой окружности, центр
которой лежит внутри треугольника АВС.
Прямые, проходящие через точку
,
касаются окружности в точках
и
.
Найдите площадь треугольника DBE,
если АВ=ВС=2,
,
а радиус окружности равен 1.
Решение. Выполним чертеж:
Так
как точки
и
лежат на окружности, то
.
Следовательно, точка
лежит на срединном перпендикуляре к
отрезку
,
который в равнобедренном треугольнике
совпадает с высотой, медианой и
биссектрисой. Следовательно,
является прямоугольным, откуда
и
,
так как
и, значит,
,
а
.
Теперь
и
.
Поскольку
является прямоугольным, то
.
Далее,
,
так они являются отрезками касательных,
проведенных к окружности из одной точки,
поэтому
.
Так как
,
то
,
ибо
,
а
.
Следовательно,
.
#
Решить задачи:
17)
В треугольнике
сторона
равна 5м,
разность сторон
и
равна 2м, а угол
вдвое больше угла
.
Найти длины сторон
и
.
18)
В треугольнике
сторона
равна 5см, сумма
двух других сторон равна 10см,
а угол
в два раза больше угла
.
Найти длины сторон
и
.
19)
В равнобедренном треугольнике ABC
имеем:
AB=BC=8см,
AC=12см. На
стороне АВ
задана точка
Е так, что
ВЕ:АЕ=3:1.
Найдите
.
20)
В равнобедренном треугольнике АВС
имеем:
АВ=ВС=15м,
АС=20м. На
стороне ВС
задана точка
Е так, что
ВЕ:СЕ=1:4.
Найдите
.
10 задание
1) При решении уравнений данного параграфа полезными окажутся следующие формулы:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
Решить уравнения:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
;
16)
.
2) Вторая часть задания содержит задачи на составление уравнений.
Решить задачи:
17)
Трое рабочих разной квалификации
выполнили некоторую работу, причем
первый работал 6
ч, второй – 4
ч и третий – 7
ч. Если бы первый рабочий работал 4
ч, второй – 2
ч и третий – 5 ч,
то было бы выполнено лишь
всей работы. За сколько часов рабочие
закончили бы работу, если бы они работали
все вместе одно и то же время?
18)
Бак вместимостью
наполняется топливом. При опорожнении
этого же бака производительность насоса
на
выше, чем производительность насоса
при наполнении. В результате время
опорожнения бака на 8
мин меньше времени заполнения. Определите
производительность насоса при наполнении
бака.
19)
Бассейн наполняется водой из двух
кранов. Сначала первый кран был открыт
того времени, за которое наполняет
бассейн один второй кран. Затем, наоборот,
один второй кран был открыт
того времени, за которое наполняет
бассейн один первый кран. После этого
оказалось наполненным
бассейна. Оба крана, открытые вместе,
наполняют бассейн за 2,4
ч. За какое время наполнит бассейн каждый
кран в отдельности?
20) В бассейн проведены четыре трубы. Когда открыты первая, вторая и третья трубы, бассейн наполняется за 12 мин; когда открыты вторая и четвертая трубы – за 15 мин; когда открыты только первая, третья и четвертая трубы – за 20 мин. За какое время наполнится бассейн, если открыть все четыре трубы?
11 задание
1) Первая часть задания посвящена решению тригонометрических уравнений.
Решить уравнения:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
.
2) Вторая часть задания содержит задачи по планиметрии.
Пример 1. Найти величины углов треугольника, если их тангенсы – последовательные целые числа.
Решение.
Пусть
,
и
- величины углов треугольника. По условию
задачи
,
и
,
где
.
По формуле приведения
,
поэтому
.
Решая полученное уравнение, получаем
При
имеем
и
,
что невозможно, так как треугольник не
может иметь двух тупых углов. При
имеем
,
что невозможно, так как
,
где
.
При
получаем
,
и
,
так что
,
и
.
Так как
,
то
и, значит,
.
Следовательно, найденные углы
,
и
являются искомыми. #
Решить задачи:
16) Найти углы треугольника, если котангенсы половин этих углов – последовательные целые числа.
17) Около окружности радиуса R описана трапеция ABCD, длина меньшего основания BC которой равна а. Пусть E – точка касания окружности со стороной AB, а длина отрезка BE равна b. Найдите площадь трапеции.
18)
Имеется квадрат ABCD
и точка О,
лежащая в плоскости квадрата, но вне
его. Известно, что ОА=ОВ=5,
.
Найдите площадь квадрата ABCD.
19)
Площадь квадрата ABCD
больше 225.
В плоскости квадрата есть точка О,
такая, что OB=OD=13,
.
Найдите сторону квадрата и выясните,
где расположена точка О
– вне или
внутри квадрата ABCD.
20)
На какие части делит гипотенузу
треугольника
точка, одинаково удаленная от его
катетов, если длина гипотенузы равна
60см, а косинус
одного из острых углов треугольника
равен 0,8?
12 задание
1) При решении тригонометрических уравнений нередко полезным оказывается метод введения дополнительного угла:
Пример
1. Решить
уравнение:
.
Решение.
Если
,
то решением уравнения будет любое
действительное число
.
Если
,
а
,
то решений нет. Пусть теперь
.
Так как
,
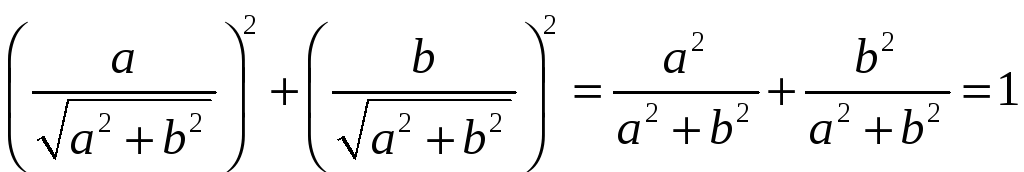то
существует единственный угол
такой, что
,
а
:
Теперь имеем:
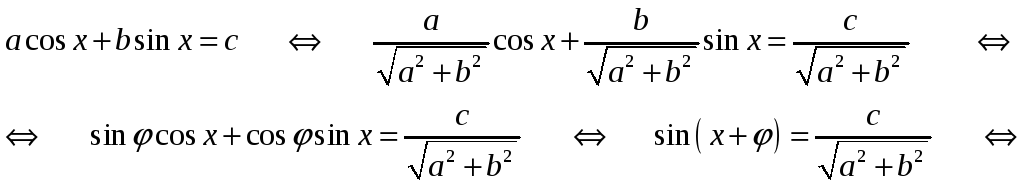
Таким
образом,
,
если
,
и
,
если
.
Отметим, что можно было взять
и
.
#
Решить уравнения:
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
;
12)
;
13)
;
14)
;
15)
.
2)
Вторая часть
задания посвящена задачам на бесконечно
убывающую геометрическую прогрессию.
Напомним, что геометрическая прогрессия
,
,
,
…,
,
… называется бесконечно
убывающей,
если
.
Сумма
членов бесконечно убывающей геометрической
прогрессии:
.
Пример 2. Найдите знаменатель бесконечно убывающей геометрической прогрессии, у которой каждый член в 5 раз больше суммы всех ее последующих членов.
Решение.
По условию задачи
,
поэтому
и
.
#
Решить задачи:
16) Найдите первый член и знаменатель бесконечно убывающей геометрической прогрессии, сумма первых двух членов которой равна 48, а сумма всех членов равна 49.
17)
Найдите третий член бесконечно убывающей
геометрической прогрессии, сумма которой
равна 1,6, а
второй член равен
.
18) Найдите знаменатель бесконечно убывающей геометрической прогрессии, если ее сумма в 3 раза больше суммы трех ее первых членов.
19)
Даны первые два члена бесконечно
убывающей геометрической прогрессии:
и
.
Найдите знаменатель и сумму этой
прогрессии.
20)
Сумма
бесконечно убывающей геометрической
прогрессии на 2
больше суммы первых четырех членов этой
прогрессии. Сумма первых восьми членов
прогрессии равна 4.
Найдите
.
13 задание
1) Тригонометрические неравенства удобно решать с использованием единичной окружности.
Пример
1. Решить
неравенство:
.
Решение. Для нахождения решений неравенства используем единичную окружность:
