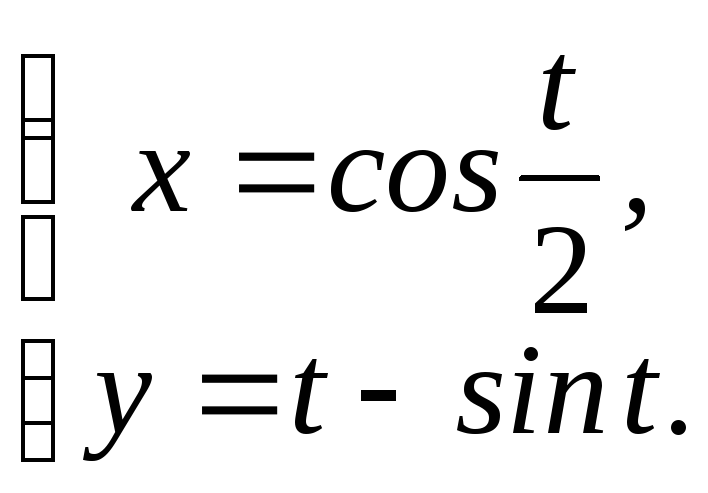- •Глава . Производная и ее применение
- •§1. Производная функции
- •1. Определение производной
- •2. Действия над дифференцируемыми функциями
- •4. Производная функции, заданной параметрически
- •5. Дифференцирование показательно-степенной функции
- •6. Производные высших порядков
- •8. Теоремы Ферма, Ролля, Коши и Лагранжа
- •10. Формула Тейлора
- •10.1. Формула Тейлора для многочленов
- •10.2. Формула Тейлора для произвольной функции
- •10.3. Форма Пеано остаточного члена формулы Тейлора
- •10.4. Форма Лагранжа остаточного члена формулы Тейлора
- •10.5. Представление по формуле Маклорена элементарных функций
- •11. Формула Тейлора и эквивалентные бесконечно малые. Вычисление пределов с помощью формулы Тейлора
- •12. Приближённые вычисления с помощью формулы Тейлора
- •§2. Исследование поведения функций и ее построение ее графика
- •1. Промежутки монотонности функции
- •2. Экстремумы функции
- •3. Направление выпуклости функции. Точки перегиба
- •4. Асимптоты графика функции
- •Так как то горизонтальных асимптот нет.
- •5. Исследование функции и построение ее графика
- •Вопросы промежуточного контроля
2. Действия над дифференцируемыми функциями
Пусть
С
– постоянная,
![]() и
и![]() - дифференцируемые функции. Тогда
- дифференцируемые функции. Тогда
(С f (x)) = С f (x),
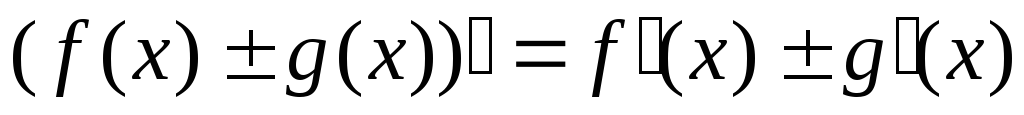 ,
,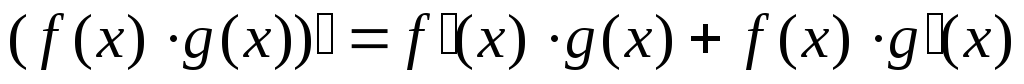 ,
,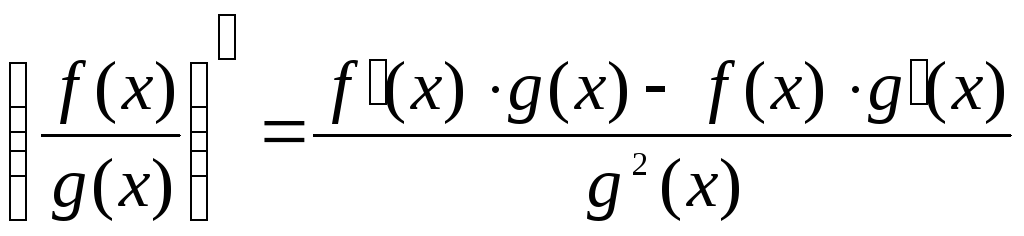 ,
,
Таблица производных некоторых функций
|
1.
|
2.
|
3.
|
|
4.
|
5.
|
6.
|
|
7.
|
8.
|
9.
|
|
10.
|
11.
|
12.
|
|
13.
|
14.
|
15.
|
|
16.
|
17.
|
18.
|
|
19.
|
20.
|
21.
|
Типовой пример
Используя определение производной, найти производную функции y = sin (2x + 1).
►Придадим значению переменной x приращение x, тогда функция y получит приращение
y = f(x + x) – f(x) = sin (2(x + x) + 1) – sin (2x + 1) =
![]()
= 2 sin x cos (2x + x + 1).
Отсюда находим
![]()
![]() .
.
Таким
образом,
![]() .
◄
.
◄
Типовой пример
Найти
производную функций: а)
у=х4,
б)
у =![]() ,
,
в)
у =![]() ,г)
у =
,г)
у =![]() .
.
►а) По формуле 4 таблицы при n = 4 имеем у = (х4) = 4 х3.
б)
у =![]() По формуле 4 таблицы приn
= – 4 имеем
у
=(х–4)=
– 4 х–5=
По формуле 4 таблицы приn
= – 4 имеем
у
=(х–4)=
– 4 х–5=![]()
в)
у =
![]() .
По формуле 4 таблицы приn
=5/3 имеем
у=
.
По формуле 4 таблицы приn
=5/3 имеем
у=![]()
г)
у =![]() Так какsin5
не зависит от x
(т.е. sin5=const),
то формуле (1) таблицы (sin5)=0.
По свойству (1) имеем у′
=
Так какsin5
не зависит от x
(т.е. sin5=const),
то формуле (1) таблицы (sin5)=0.
По свойству (1) имеем у′
=![]() =
=![]() ◄
◄
Типовой пример
Найти производную функций: а) y=ex + x2 sinx,
б)
![]()
►а) По свойству (2) имеем у=(ex) + (x2 sinx). По формуле 6 таблицы и свойству (3) имеем у=ex + (x2)sinx + x2 (sinx) = ex + 2x sinx + x2 cosx.
б)
По свойству
(4) имеем
![]()
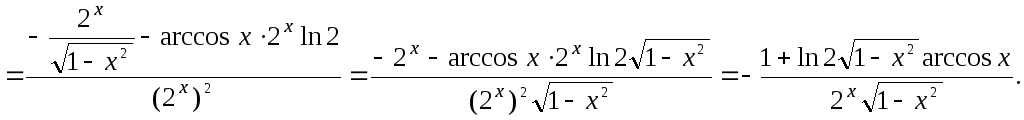
◄
3. Дифференцирование сложной функции
Пусть
функция
![]() имеет производную в точкеu,
а функция u
= g(x)
имеет производную в точке u
=
g(x).
Тогда сложная функция
имеет производную в точкеu,
а функция u
= g(x)
имеет производную в точке u
=
g(x).
Тогда сложная функция
![]() имеет производную в точкеx,
равную
имеет производную в точкеx,
равную
![]() .
(2)
.
(2)
Типовые примеры
Найти производную функции.
1)
![]() .
.
►Применяя
формулу (2), имеем ![]()
![]() . ◄
. ◄
2)![]() .
.
►![]()
![]() .◄
.◄
4. Производная функции, заданной параметрически
Пусть функции
![]()
![]()
задают
параметрически функцию y
= f(x)
в окрестности точки x
=![]() ,
функции
,
функции![]() и
и![]() имеют производные
имеют производные![]() и
и![]() в точкеt.
Тогда функция
в точкеt.
Тогда функция
![]() также имеет производную в точкеx,
и верна формула
также имеет производную в точкеx,
и верна формула
![]() .
(3)
.
(3)
Типовой пример
x=
sin
2t,
y
= tg
2t
(– π
⁄ 4 < t
<
π
⁄ 4). Найти
![]() .
.
►По
формуле (3) имеем
 ◄
◄
5. Дифференцирование показательно-степенной функции
Для
дифференцирования
показательно-степенной
функции y
=![]()
![]() ,
где
,
где![]() и
и![]()
дифференцируемые в точке
дифференцируемые в точке
![]() функции, можно представить ее в виде
функции, можно представить ее в виде
![]() .
.
Затем дифференцировать ее как сложную функцию:
![]() .
(4)
.
(4)
Типовые примеры
Найти производную функции.
1)
![]() .
.
►Это
степенно-показательная функция. Для
дифференцирования рациональнее сначала
ее прологарифмировать:
![]() .
Диффренцируем обе части равенства:
.
Диффренцируем обе части равенства:![]() ,
т.е.
,
т.е.![]() ,
а следовательно,
,
а следовательно,![]() .◄
.◄
2)
![]() .
.
►Для дифференцирования такой достаточно громоздкой функции ее тоже рациональнее сначала прологарифмировать:
![]() .
.
Дифференцируем обе части равенства:
![]() ,
,
![]() .
.
Следовательно:
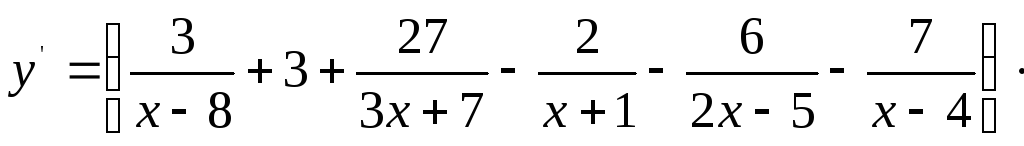
![]() .◄
.◄
6. Производные высших порядков
Пусть
функция
![]() имеет производную
имеет производную![]() в каждой точке
в каждой точке![]() некоторого множества
некоторого множества![]() .
Тогда ее производную
.
Тогда ее производную![]() можно рассматривать как функцию,
определенную на множестве
можно рассматривать как функцию,
определенную на множестве![]() .
В свою очередь функция
.
В свою очередь функция![]() может в некоторых точках множества
может в некоторых точках множества![]() иметь производную. В этом случае
производной второго порядка (второй
производной) называется производная
от производной
иметь производную. В этом случае
производной второго порядка (второй
производной) называется производная
от производной![]() .
Для второй производной функции
.
Для второй производной функции![]() в точкеx
применяются обозначения:
в точкеx
применяются обозначения:
![]()
Аналогично
определяются производные 3-го, 4-го, и
т.д. порядков. Производной первого
порядка (или первой производной) считается
![]() .
.
Типовой пример
y = sin 3x. Найти производные 1-го, 2-го, 3-го порядков и y(3)(π). ►y = 3 cos 3x, y = – 9sin 3x, y(3) = – 27 cos 3x, y(3)(π) = – 27 cos 3π = 27. ◄
Типовой пример
Найти dy, df (2), df (2) при dx=0.2, если y = ln (1 + x2).
►По
формуле (1) dy
= f
(x)
dx
=
![]() Приx
= 2 имеем d f
(2) =
Приx
= 2 имеем d f
(2) =![]() Приdx
= 0,2 имеем
Приdx
= 0,2 имеем
![]() ◄
◄
Типовые примеры
Найти производные от функций:
|
а)
|
б)
|
в)
|
|
г)
|
д)
|
е)
|
Используя правила дифференцирования и таблицу производных, найдем производные данных функций:
►а)
![]() .
.
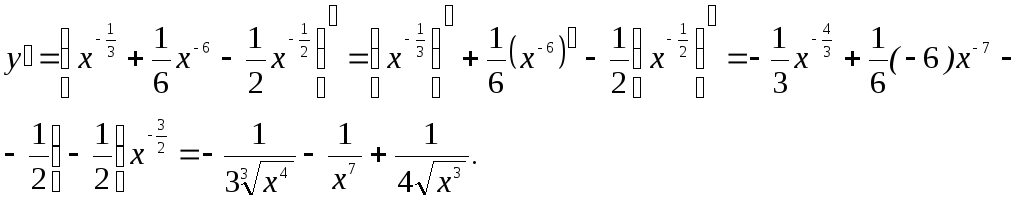
Ответ:
![]() ◄
◄
►б)![]() .
.
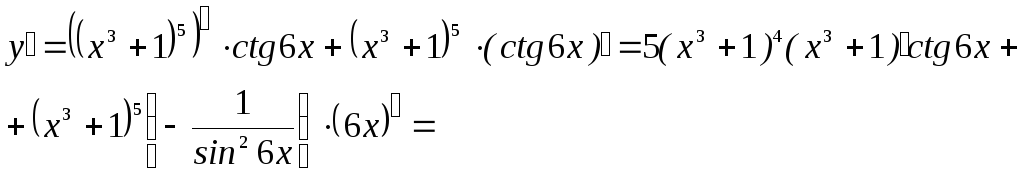
![]()
Ответ:
![]() ◄
◄
►в)
![]() .
.
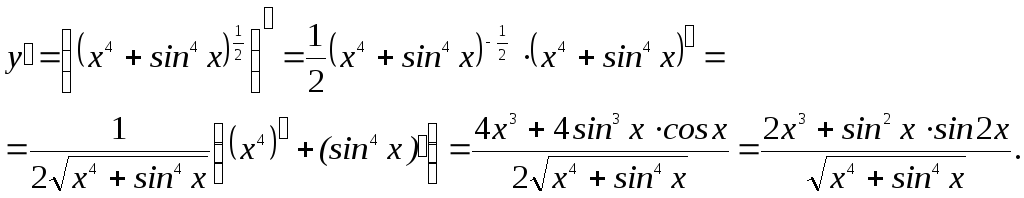
Ответ:
![]() ◄
◄
►г)
![]() .
Данная функция является степенно-показательной.
Применим метод логарифмического
дифференцирования. Прологарифмируем
функцию:
.
Данная функция является степенно-показательной.
Применим метод логарифмического
дифференцирования. Прологарифмируем
функцию:
![]() .
Применим свойство логарифмов:
.
Применим свойство логарифмов:
![]() .
Тогда
.
Тогда![]() .
Дифференцируем обе части равенства по
.
Дифференцируем обе части равенства по![]() :
:
![]() ;
;![]() ;
;![]() ;
;
![]() .
.
Ответ:
![]() .◄
.◄
►д)
![]() .
Функция задана неявно в виде
.
Функция задана неявно в виде![]() .
Дифференцируем обе части данного
уравнения, считая
.
Дифференцируем обе части данного
уравнения, считая![]() функцией от
функцией от![]() :
:![]() .
.
Выразим
из уравнения
![]() :
:![]() ;
;
![]() .
.
Ответ:
![]() .◄
.◄
►е)
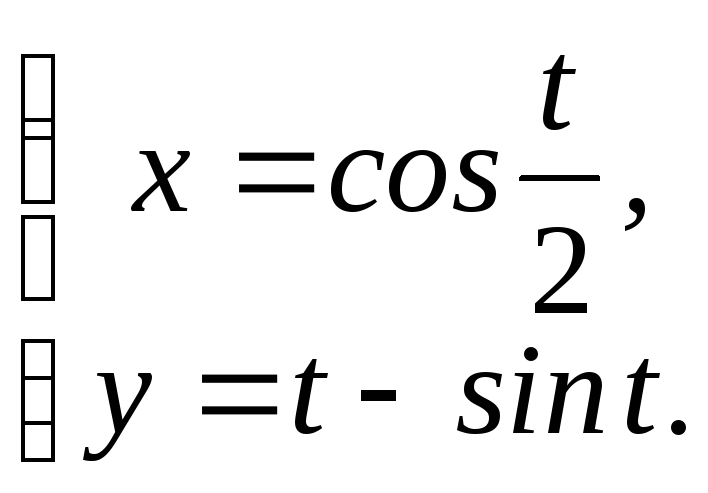 Функция
задана параметрически
Функция
задана параметрически![]() Производная такой функции находится
по формуле:
Производная такой функции находится
по формуле:![]() .
.
![]()
![]()

Ответ:
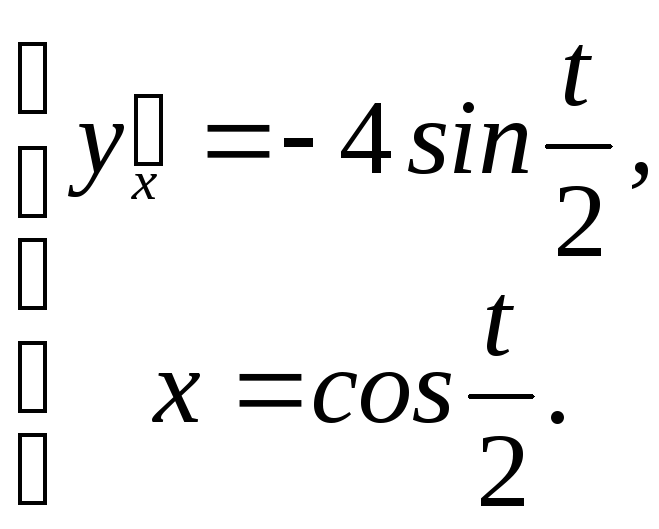 ◄
◄
Типовой пример
Найти
![]() ,
еслиy
= ln(sinx)
.
,
еслиy
= ln(sinx)
.
►![]() ;
;
![]()
![]() .◄
.◄
Типовой пример
Доказать, что
![]() =
sin
=
sin![]() ,
,
![]()
N.
N.
►Доказательство
проведём методом математической индукции
(индукция может быть неполной, полной
и математической), который заключается
в следующем: проверяется утверждение
при
![]() = 1; если из предположения, что оно верно
приn
следует, что оно верно и при
= 1; если из предположения, что оно верно
приn
следует, что оно верно и при
![]() + 1, то делается вывод, что утверждение
верно при любом натуральном
+ 1, то делается вывод, что утверждение
верно при любом натуральном![]() .
Итак, проверим данную формулу при
.
Итак, проверим данную формулу при![]() = 1 .
= 1 .
![]() = cos
= cos![]() = sin
= sin![]() .
Формула выполняется. Пусть данное
соотношение верно при
.
Формула выполняется. Пусть данное
соотношение верно при
![]() .
Найдём (
.
Найдём (![]() + 1)-ю производную.
+ 1)-ю производную.
![]() =
=
![]() =
=
=
=![]() = cos
= cos![]() = =sin
= =sin![]() .
Как видно, формула верна и при
.
Как видно, формула верна и при
![]() +1,
следовательно, по методу математической
индукции она верна при любом натуральном
+1,
следовательно, по методу математической
индукции она верна при любом натуральном![]() .
◄
.
◄
Можно доказать, что
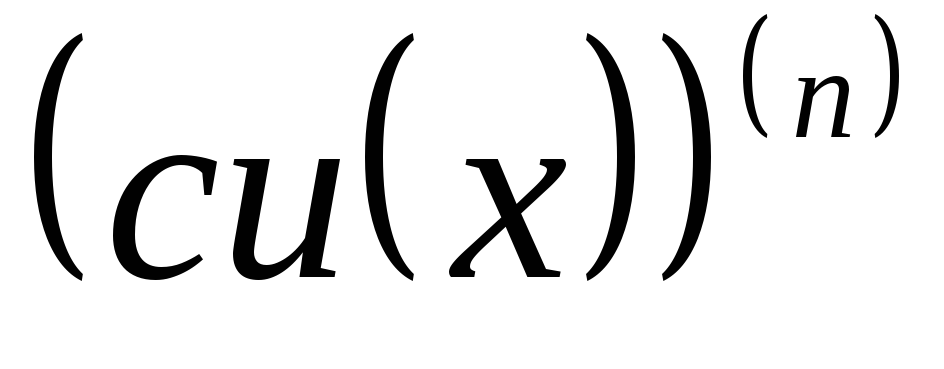 =
=
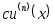 ,
,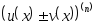 =
=
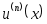
 ,
,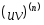 =
=
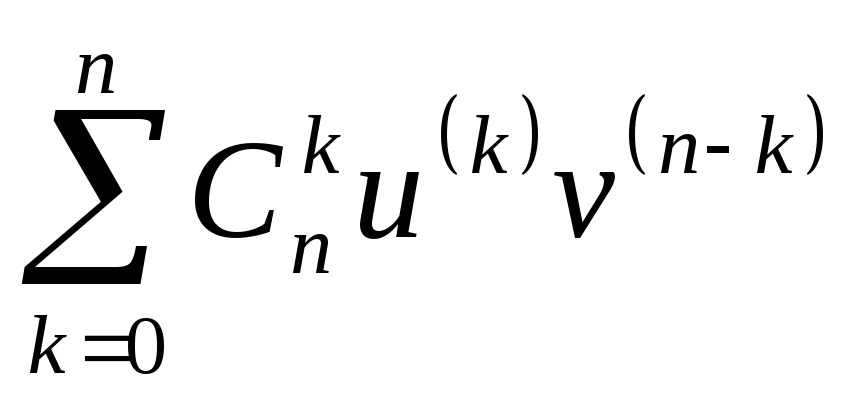 .
.
Последняя
формула называется формулой
Лейбница.
Она напоминает бином Ньютона, при этом
![]() =
=![]() .
.
Типовой пример
Найти
![]() -ю
производную функции
-ю
производную функции
![]() =
=
![]()
![]() .
.
►Воспользуемся
формулой Лейбница. Пусть
![]() = =
= =![]() ,
тогда
,
тогда![]() = 2
= 2![]() ,
,
![]() = 2,
= 2,![]() = 0 и все последующие производные равны
нулю. Пусть
= 0 и все последующие производные равны
нулю. Пусть
![]() =
=
![]() ,
т.к.
,
т.к.![]() =
=![]() ,
то по формуле Лейбница получим
,
то по формуле Лейбница получим
![]() =
=
![]()
![]()
![]() +
+
![]() 2
2![]()
![]() +
+
![]() 2
2![]() =
=
![]()
![]() .
.
Типовой пример
Найти
вторую производную от функции,
заданной параметрически
![]() =
=
![]() ,
,
![]() =
=
![]() ,
,
![]()
E.
E.
► Если
функция y
= y(x)
задана параметрическими уравнениями
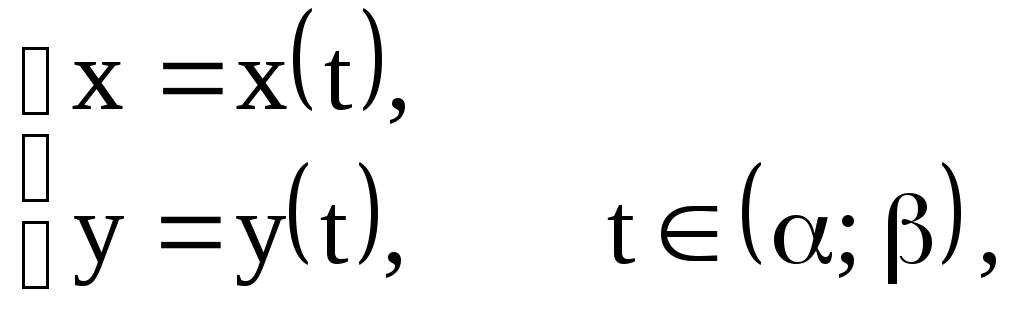 то при условии существования производных
то при условии существования производных
![]() ,
,
![]() и
и
![]() существует производная
существует производная![]() и при этом
и при этом![]() .
Вторая производная
.
Вторая производная
![]() находится по формуле
находится по формуле
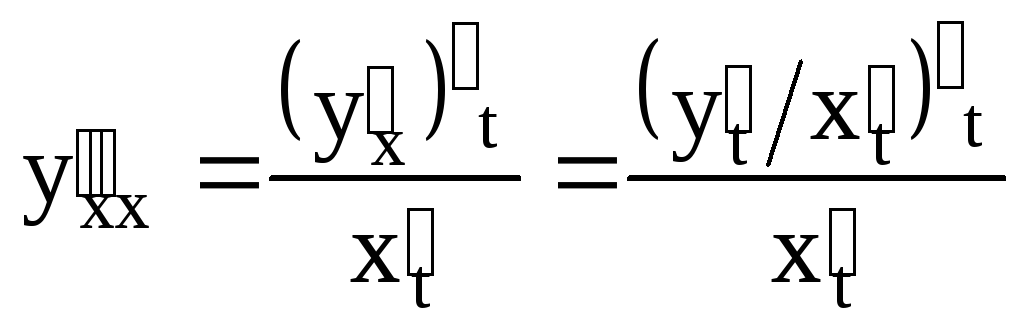 ,
или (что то же самое)
,
или (что то же самое) 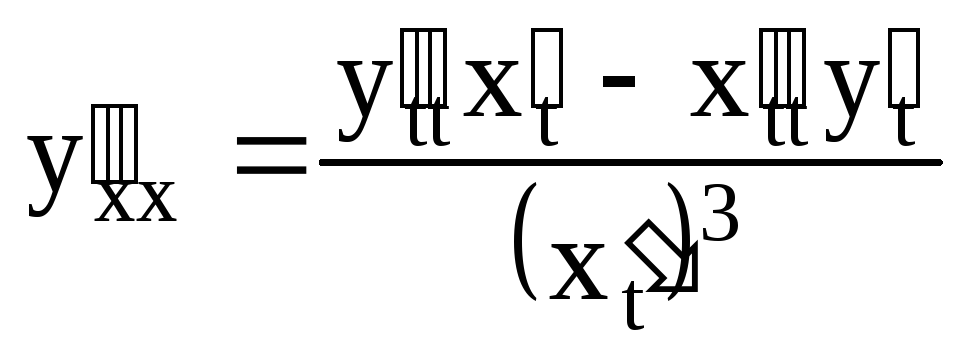 .◄
.◄
Типовой пример
Найти
![]() ,
,![]() ,
если
,
если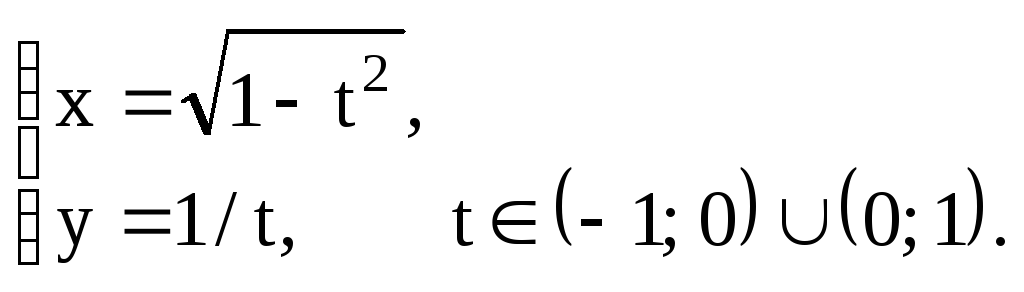
►Имеем:
![]() ;
;
![]() ;
;
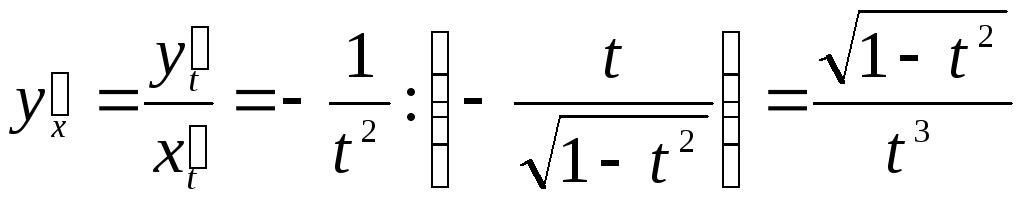 ;
;
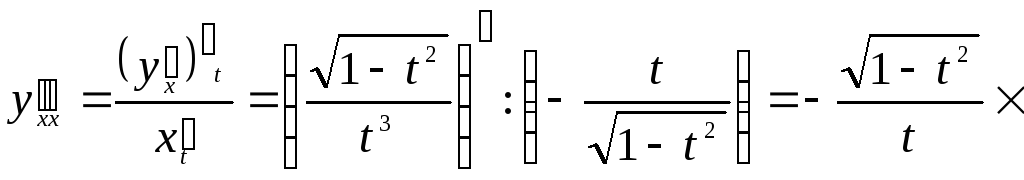
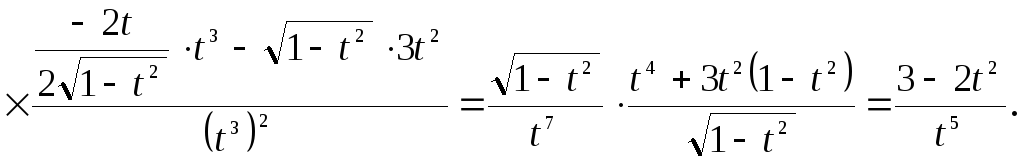 ◄
◄
Говорят, что уравнение
![]()
неявно
задаёт функцию
![]() в интервале
в интервале![]() ,
если для любого
,
если для любого![]() уравнение
уравнение![]() имеет единственное решение
имеет единственное решение![]() .
.
Для
нахождения производной функции
![]() ,
заданной неявно данным уравнением,
следует продифференцировать обе части
равенства, считая
,
заданной неявно данным уравнением,
следует продифференцировать обе части
равенства, считая![]() функцией от
функцией от![]() ;
затем полученное уравнение, в которое
будут входить
;
затем полученное уравнение, в которое
будут входить![]() и
и![]() ,
следует разрешить относительно
,
следует разрешить относительно![]() .
Для нахождения
.
Для нахождения![]() исходное равенство дифференцируется
дважды, в результате чего получается
уравнение, содержащее
исходное равенство дифференцируется
дважды, в результате чего получается
уравнение, содержащее![]() ,
,![]() ,
,![]() ,
которое следует разрешить относительно
,
которое следует разрешить относительно![]() ,
затем вместо
,
затем вместо![]() подставить функцию от
подставить функцию от![]() и
и![]() ,
найденную указанным выше способом.
,
найденную указанным выше способом.
Типовой пример
Найти
значения
![]() ,
,![]() ,
если функцияy
задана неявно уравнением
,
если функцияy
задана неявно уравнением
![]() .
.
►Считая
y
функцией от x,
продифференцируем обе части равенства:
![]() ;
;
![]() ;
;
![]() .
Отсюда находим
.
Отсюда находим
![]() ;
;
![]() .
Для нахождения y(0)
в исходном равенстве положим x
= 0:
.
Для нахождения y(0)
в исходном равенстве положим x
= 0:
![]() ;
; ![]() ;
y(0)
= 1. Таким образом,
;
y(0)
= 1. Таким образом, ![]() .
.
Найдём
![]() ,
для чего продифференцируем равенство
,
для чего продифференцируем равенство![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
Подставив
в последнем равенстве вместо
![]() выражение
выражение![]() ,
получим
,
получим
![]() ,
откуда находим
,
откуда находим
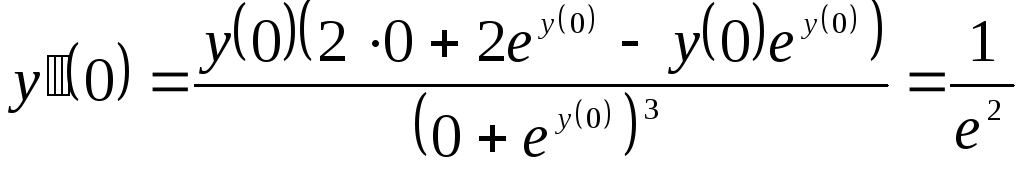 .◄
.◄
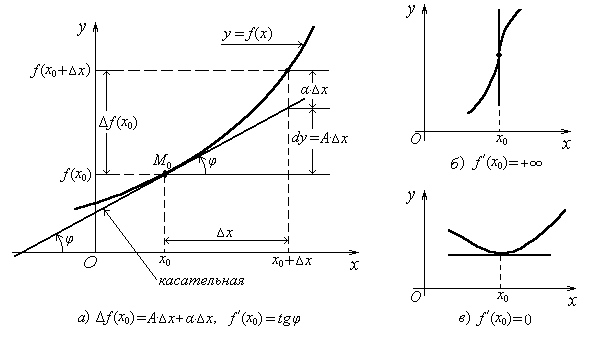
7. Геометрический смысл производной. Касательная и нормаль к кривой
Пусть
![]()
дифференцируемая в точке x0
функция,
M0
точка на графике этой функции с
координатами x0
и y0=
f(x0),
дифференцируемая в точке x0
функция,
M0
точка на графике этой функции с
координатами x0
и y0=
f(x0),
![]()
угловой
коэффициент касательной,
проведенной к графику функции
угловой
коэффициент касательной,
проведенной к графику функции
![]() в точкеM0,
в точкеM0,
![]()
![]()
угол наклона касательной к оси абсцисс
(рис 1а).
Геометрический смысл производной
состоит в том, что f
(x0)
= k.
Уравнение
касательной
к графику функции
угол наклона касательной к оси абсцисс
(рис 1а).
Геометрический смысл производной
состоит в том, что f
(x0)
= k.
Уравнение
касательной
к графику функции
![]() в точкеM0
имеет вид
в точкеM0
имеет вид
![]() .
(5)
.
(5)
Прямая,
перпендикулярная к касательной и
проходящая через точку касания, называется
нормалью к
графику функции
![]() в этой точке.
в этой точке.
Уравнение
нормали к графику функции
![]() в точкеM0
(x0
, y0)
имеет вид
в точкеM0
(x0
, y0)
имеет вид
![]() .
(6)
.
(6)
Замечание
Пусть![]() =+∞
(или – ∞). Тогда касательная к графику
функции
=+∞
(или – ∞). Тогда касательная к графику
функции![]() в точкеM0
параллельна
оси Оу,
а уравнение касательной имеет вид х=x0
(рис.1б).
в точкеM0
параллельна
оси Оу,
а уравнение касательной имеет вид х=x0
(рис.1б).
Замечание
Если
![]() =0,
то касательная к графику функции
=0,
то касательная к графику функции![]() в точкеM0
параллельна оси Ох
(рис.1в).
в точкеM0
параллельна оси Ох
(рис.1в).
Рис.
1
Найти уравнения касательной и нормали к параболе y = x2 в точке с абсциссой 2.
►Пусть x0=2, f(x) = x2 . Тогда , f(x0) = 4, f (x) = 2x, f (x0) = 4. По формуле (5) получаем уравнение касательной: y – 4 = 4(x – 2) или y 4x + 4 = 0. По формуле (6) получаем уравнение нормали: 4(y – 4) + x – 2 = 0 или x + 4 y 18 = 0. ◄
Типовой пример
В
каких точках графика функции
![]() касательная к нему параллельна прямой
касательная к нему параллельна прямой![]() ?
Сделать рисунок.
?
Сделать рисунок.
►По
условию касательные к графику и заданная
прямая параллельны, поэтому угловые
коэффициенты этих прямых равны между
собой. Угловой коэффициент прямой
![]()
![]() .
Угловой коэффициент касательной к
кривой в некоторой точке
.
Угловой коэффициент касательной к
кривой в некоторой точке![]() находим из геометрического смысла
производной:
находим из геометрического смысла
производной:
![]() ,где -
угол наклона касательной к графику
функции
,где -
угол наклона касательной к графику
функции
![]() в точке
в точке![]() .
.
![]() .
.
Для
нахождения угловых коэффициентов
искомых прямых составим уравнение
![]() .
Решив его, найдем абсциссы двух точек
касания:
.
Решив его, найдем абсциссы двух точек
касания:![]() и
и![]() .
Из уравнения кривой определяем ординаты
точек касания:
.
Из уравнения кривой определяем ординаты
точек касания:![]() и
и![]() .
Сделаем рис. 2.
.
Сделаем рис. 2.
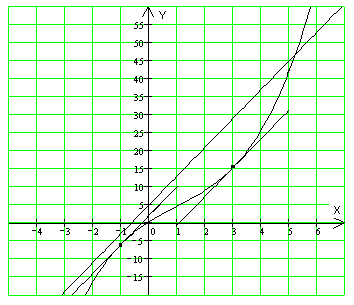
Рис. 2
Ответ:
(-1;-6) и
![]() .◄
.◄
Типовой пример
Найти
площадь треугольника, образованного
прямой
![]() ,
касательной и нормалью, проведёнными
к графику функции
,
касательной и нормалью, проведёнными
к графику функции![]() в точке с абсциссой
в точке с абсциссой![]() и ординатой
и ординатой![]() .
.
►Найдём
ординату y0
точки касания и
![]() :
:
![]() ;
;
![]() ;
;
![]() .
.
У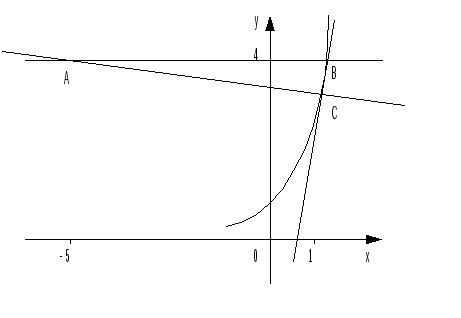 равнением
касательной является
равнением
касательной является![]() или
или![]() .Уравнение
нормали имеет вид
.Уравнение
нормали имеет вид
![]() или
или![]() .
Найдём координаты точек А и В (см. рис).
.
Найдём координаты точек А и В (см. рис).
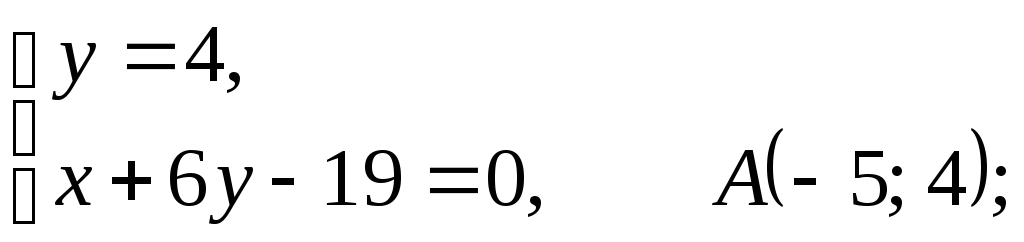
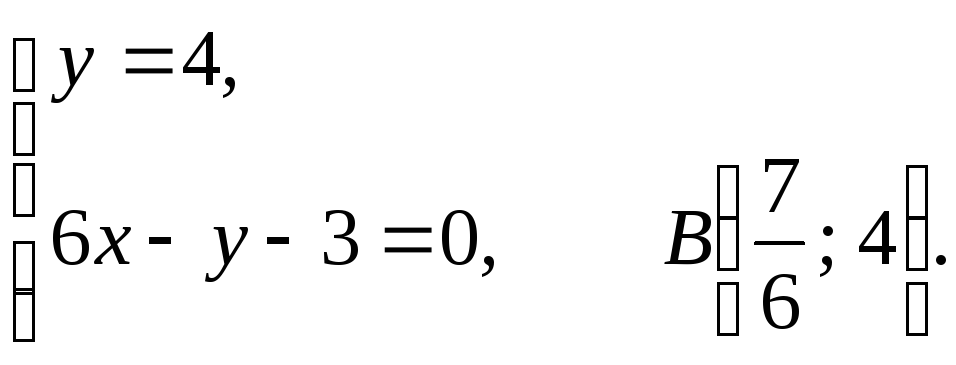
Вычислим длины катетов АС и ВС прямоугольного треугольника АВС:
![]() ,
,
![]() .
.
По
этим данным найдём искомую площадь ![]() ◄
◄