
13. Общие свойства числовых пределов
В данном параграфе мы рассмотрим свойства пределов числовых сетей и их интерпритации для конкретных примеров. Изучение общих свойств пределов мы начнем со свойства единственности предела.
Теорема
13.1. Если
предел числовой сети
![]() существует, то он единственен.
существует, то он единственен.
Доказательство.
Предположим
противное. Тогда существуют, по крайней
мере, две различные точки
![]() и
и![]() из расширенной числовой прямой такие,
что
из расширенной числовой прямой такие,
что![]() и
и![]() .
По лемме Хаусдорфа (см. лемму 10.1) найдется
такое число
.
По лемме Хаусдорфа (см. лемму 10.1) найдется
такое число![]() ,
что
,
что![]() .
Применяя теперь определение предела
сети, найдем такие индексы
.
Применяя теперь определение предела
сети, найдем такие индексы![]() ,
что
,
что![]() для всех
для всех![]() и
и![]() для всех
для всех![]() .
По направленности вверх множества
.
По направленности вверх множества![]() найдется такой индекс
найдется такой индекс![]() ,
что
,
что![]() и
и![]() .
Тогда для всех
.
Тогда для всех![]() будет
будет![]() и
и![]() ,
чего быть не может, так как
,
чего быть не может, так как![]() .
#
.
#
Из этой теоремы вытекает единственность предела числовой последовательности, предела функции в точки, производной, нижнего и верхнего интегралов и интеграла Римана, если они существуют.
Семейство
![]() называется
подсетью
числовой
сети
называется
подсетью
числовой
сети
![]() ,
если
,
если![]() и для любого
и для любого![]() найдется такой индекс
найдется такой индекс![]() ,
что
,
что![]() .
Если
.
Если
![]() ,
то
,
то![]() ,
поэтому найдется такой индекс
,
поэтому найдется такой индекс![]() ,
что
,
что![]() и
и![]() .
Далее найдется такой индекс
.
Далее найдется такой индекс![]() ,
что
,
что![]() .
Следовательно,
.
Следовательно,![]() и
и![]() ,
так чтомножество
,
так чтомножество
![]() ,
наделенное тем же отношением предпорядка,
что и
,
наделенное тем же отношением предпорядка,
что и![]() ,
является предупорядоченным и направленным
вверх
множеством. Это означает, что подсеть
,
является предупорядоченным и направленным
вверх
множеством. Это означает, что подсеть
![]() также
является
сетью.
Подсети играют в теории пределов роль,
аналогичную подпоследовательностям.
также
является
сетью.
Подсети играют в теории пределов роль,
аналогичную подпоследовательностям.
Теорема
13.2.
Пусть
![]() - некоторая числовая сеть, а
- некоторая числовая сеть, а![]() - ее подсеть. Если существует
- ее подсеть. Если существует![]() ,
то
,
то
![]() .
.
Доказательство.
Пусть
![]() .
По определению предела числовой сети
найдется
такой индекс
.
По определению предела числовой сети
найдется
такой индекс
![]() ,
что
,
что![]() для всех индексов
для всех индексов![]() таких, что
таких, что![]() . По
определению подсети найдется такой
индекс
. По
определению подсети найдется такой
индекс
![]() ,
что
,
что![]() .
Тогда
.
Тогда
![]() для всех индексов
для всех индексов![]() таких, что
таких, что![]() ,
так что
,
так что![]() .
#
.
#
Если
![]() - некоторая последовательность
действительных чисел, тодля
построения
ее подпоследовательностей
используется
та же идея, что и для построения подсетей.
Для этого выбирается бесконечное
подмножество
- некоторая последовательность
действительных чисел, тодля
построения
ее подпоследовательностей
используется
та же идея, что и для построения подсетей.
Для этого выбирается бесконечное
подмножество
![]() в
в![]() ,
которое наследует упорядоченность из
множества натуральных чисел, а затем
точкам множества
,
которое наследует упорядоченность из
множества натуральных чисел, а затем
точкам множества![]() приписываются новые номера так, чтобы
получаемый новый порядок индексов
соответствовал прежнему порядку. Новые
индексы обычно записываются в виде
приписываются новые номера так, чтобы
получаемый новый порядок индексов
соответствовал прежнему порядку. Новые
индексы обычно записываются в виде![]() .
При этом
.
При этом![]() обозначает номер в исходной упорядоченности
(т.е. во множестве
обозначает номер в исходной упорядоченности
(т.е. во множестве![]() ),
а
),
а![]() обозначает новый номер. Согласованность
порядков означает, чтонеравенство
обозначает новый номер. Согласованность
порядков означает, чтонеравенство
![]() выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда
![]() .
.
Следствие.
Пусть
![]() - некоторая последовательность
действительных чисел, а
- некоторая последовательность
действительных чисел, а![]() - ее подпоследовательность. Если
- ее подпоследовательность. Если![]() ,
то
,
то
![]() .
.
Замечание.
1) Существуют
подсети числовых сетей со счетными
множествами индексов, которые не могут
быть представлены в виде последовательностей,
являющихся подсетями заданных сетей.
Действительно, пусть
![]() ,
где
,
где![]() .
Упорядочим
множество
.
Упорядочим
множество
![]() естественным образом:
естественным образом:![]() тогда и только тогда, когда
тогда и только тогда, когда![]() .
Пусть, далее,
.
Пусть, далее,
![]() -
произвольная числовая сеть и
-
произвольная числовая сеть и
![]() - множество рациональных точек из
- множество рациональных точек из![]() .
Тогда
.
Тогда
![]() -
подсеть
со счетным множеством индексов
-
подсеть
со счетным множеством индексов
![]() ,
так как по свойству плотности множества
рациональных чисел на числовой прямой
для любого действительного числа
,
так как по свойству плотности множества
рациональных чисел на числовой прямой
для любого действительного числа![]() найдется рациональное число
найдется рациональное число![]() ,
т.е. такое число
,
т.е. такое число![]() ,
что
,
что![]() .
Занумеруем теперь все точки множества
.
Занумеруем теперь все точки множества![]() произвольным образом в виде
последовательности
произвольным образом в виде
последовательности![]() .
Пусть, например,
.
Пусть, например,![]() .
По плотности множества
.
По плотности множества![]() в
в![]() найдется рациональное число
найдется рациональное число![]() .
Пусть
.
Пусть![]() .
Тогда
.
Тогда![]() и
и![]() ,
так что не существует представления
множества
,
так что не существует представления
множества![]() в виде последовательности
в виде последовательности![]() ,
при котором
,
при котором
![]() было
бы подсетью сети
было
бы подсетью сети
![]() .
.
2)
Существуют
сети, у которых нет подсетей со счетными
множествами индексов.
Например, пусть
![]() - множество всех разбиений отрезка
- множество всех разбиений отрезка![]() ,
упорядоченное по включению:
,
упорядоченное по включению:
![]() тогда и только тогда, когда
тогда и только тогда, когда![]() (см.
пример 12.8). Предположим, что существует
числовая сеть
(см.
пример 12.8). Предположим, что существует
числовая сеть
![]() ,
имеющая подсеть
,
имеющая подсеть![]() со счетным множеством индексов
со счетным множеством индексов![]() .
Представим множество
.
Представим множество![]() в виде последовательности
в виде последовательности![]() ,
а каждое разбиение
,
а каждое разбиение![]() в виде конечного набора
в виде конечного набора![]() точек этого отрезка, удовлетворяющих
условию:
точек этого отрезка, удовлетворяющих
условию:![]() .
По теореме 5.2 множество
.
По теореме 5.2 множество![]() является не более чем счетным, поэтому
существует точка
является не более чем счетным, поэтому
существует точка![]() .
Отметим, что
.
Отметим, что![]() ,
поэтому возьмем разбиение
,
поэтому возьмем разбиение![]() .
Для любого
.
Для любого![]() точка
точка![]() ,
поэтому не существует такого номера
,
поэтому не существует такого номера![]() ,
что
,
что![]() .
Следовательно,
.
Следовательно,![]() не может быть подсетью сети
не может быть подсетью сети![]() .
.
Замечание. Обращение теоремы 13.2, вообще говоря, не верно уже для последовательностей.
Пусть
![]() - некоторая числовая сеть,
- некоторая числовая сеть,![]() и
и
![]() .
Нетрудно проверить, что
.
Нетрудно проверить, что
![]() является
подсетью исходной сети.
По аналогии с остатком числового ряда
эту
подсеть будем называть
остатком
сети
является
подсетью исходной сети.
По аналогии с остатком числового ряда
эту
подсеть будем называть
остатком
сети
![]() .
Легко видеть, что справедливо следующее
частичное обращение теоремы 13.2:
.
Легко видеть, что справедливо следующее
частичное обращение теоремы 13.2:
Теорема
13.3.
Пусть
![]() - числовая сеть, а
- числовая сеть, а![]() - некоторый ее остаток. Если существует
- некоторый ее остаток. Если существует![]() ,
то
,
то
![]() .
.
Следствие.
Пусть
![]() - числовая последовательность, а
- числовая последовательность, а![]() - некоторый ее остаток. Если
- некоторый ее остаток. Если![]() ,
то
,
то
![]() .
.
В
частности из следствия теоремы 13.3
следует, что на
существование предела у числовой
последовательности и его величину не
влияет изменение первых ее
![]() членов.
членов.
Следующее утверждение часто называют теоремой о продолжении неравенств:
Теорема
13.4. Пусть
![]() - числовая сеть и
- числовая сеть и![]() .
Если точка
.
Если точка![]() такова, что
такова, что![]() (соотв.
(соотв.
![]() ),
то существует такой индекс
),
то существует такой индекс![]() ,
что
,
что![]() (соотв.
(соотв.
![]() )
для всех
)
для всех
![]() .
.
Доказательство.
Пусть, например,
![]() .
По лемме Хаусдорфа существует такое
число
.
По лемме Хаусдорфа существует такое
число![]() ,
что
,
что![]() .
Из неравенства
.
Из неравенства![]() и определения
и определения![]() окрестностей
следует, что
окрестностей
следует, что![]() для всех
для всех![]() .
Применяя теперь определение предела
сети к окрестности
.
Применяя теперь определение предела
сети к окрестности![]() ,
получим, что найдется индекс
,
получим, что найдется индекс![]() такой, что
такой, что![]() для всех
для всех![]() .
#
.
#
Следствие.
Пусть
![]() - числовая последовательность и
- числовая последовательность и![]() .
Если
.
Если![]() таково, что
таково, что![]() (соотв.
(соотв.![]() ),
то существует такой номер
),
то существует такой номер![]() ,
что
,
что![]() (соотв.
(соотв.![]() )
для всех
)
для всех
![]() .
.
Числовую
сеть
![]() будем называть
возрастающей
(соотв. убывающей),
если
будем называть
возрастающей
(соотв. убывающей),
если
![]() (соотв.
(соотв.![]() )для
всех
)для
всех
![]() таких, что
таких, что
![]() .Возрастающие
и убывающие числовые сети называются
монотонными.
Докажем
теорему
о пределе монотонных числовых сетей:
.Возрастающие
и убывающие числовые сети называются
монотонными.
Докажем
теорему
о пределе монотонных числовых сетей:
Теорема
13.5.
Любая
убывающая числовая сеть
![]() имеет
имеет![]() и любая возрастающая числовая сеть
и любая возрастающая числовая сеть![]() имеет
имеет
![]() .
.
Доказательство.
Пусть
![]() - убывающая сеть,
- убывающая сеть,![]() и
и![]() .
По критерию нижней грани (см. теорему
11.1)
.
По критерию нижней грани (см. теорему
11.1)![]() является точкой прикосновения для
множества
является точкой прикосновения для
множества![]() ,
поэтому существует такой индекс
,
поэтому существует такой индекс![]() ,
что
,
что![]() .
Тогда
.
Тогда![]() для всех
для всех
![]() и,
значит,
и,
значит,
![]() .
Это доказывает, что
.
Это доказывает, что
![]() .
Утверждение для возрастающей сети
доказывается аналогично.Замечание.
Рассмотрим в качестве числовых сетей
нижние
.
Утверждение для возрастающей сети
доказывается аналогично.Замечание.
Рассмотрим в качестве числовых сетей
нижние
![]() и
верхние
и
верхние
![]() суммы
Дарбу. В примере 12.8 равенствами
суммы
Дарбу. В примере 12.8 равенствами
![]() ,
,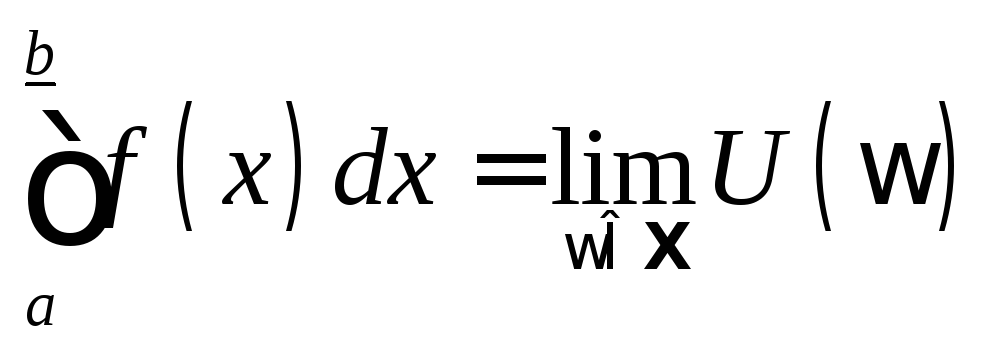
нами
были введены нижний и верхний интегралы
Дарбу. В стандартных курсах математического
анализа доказывается (применительно к
используемой здесь терминологии), что
нижние суммы Дарбу являются
возрастающими сетями, а верхние суммы
Дарбу – убывающими. Поэтому на основании
теоремы 13.5 можно заключить, что нижний
и верхний интегралы Дарбу существуют
для любой ограниченной функции
![]() ,
причем
,
причем
![]() ,
,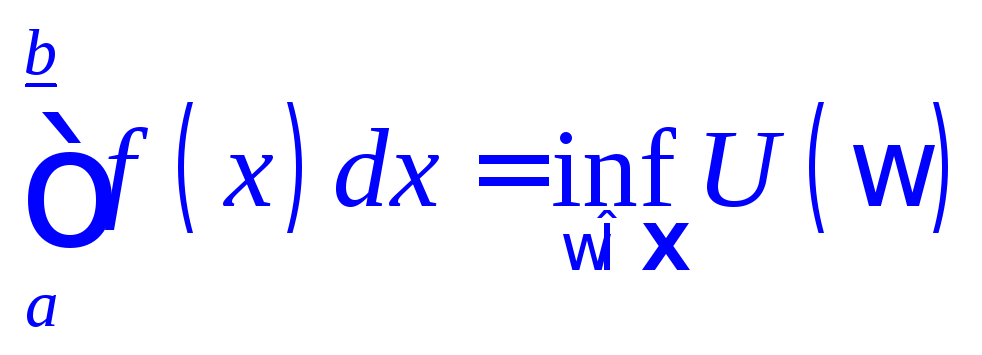 . (51)
. (51)
Именно так (с
помощью формул (51)) обычно и вводятся в
классическом математическом анализе
определения нижнего и верхнего интегралов
Дарбу. При этом, как нетрудно заметить,
для
любого разбиения
![]() и подчиненной ему выборке
и подчиненной ему выборке![]() выполняется неравенство:
выполняется неравенство:
![]() , (52)
, (52)
где
![]() - интегральная сумма (см. пример 12.9).
Более сложные соотношения устанавливает
результат, известный в литературе под
названием леммы
Дарбу:
для
любого числа
- интегральная сумма (см. пример 12.9).
Более сложные соотношения устанавливает
результат, известный в литературе под
названием леммы
Дарбу:
для
любого числа
![]() существует такое число
существует такое число![]() ,
что для любого разбиения
,
что для любого разбиения
![]() отрезка
отрезка
![]() с шагом
с шагом
![]() выполняются неравенства:
выполняются неравенства:
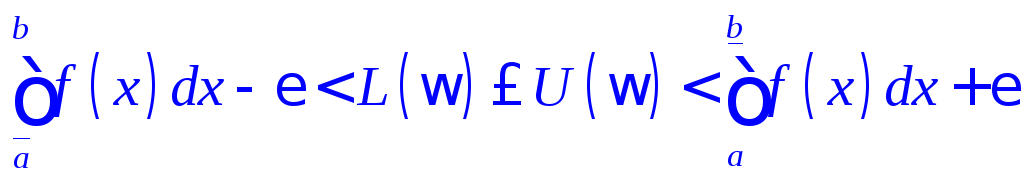 . (53)
. (53)
Из соотношений
(52) и (53) вытекает важнейший результат,
известный под названием второго
критерия интегрируемости:
для
того чтобы для ограниченной функции
![]() существовал конечный
существовал конечный
![]() ,
необходимо и достаточно, чтобы
,
необходимо и достаточно, чтобы
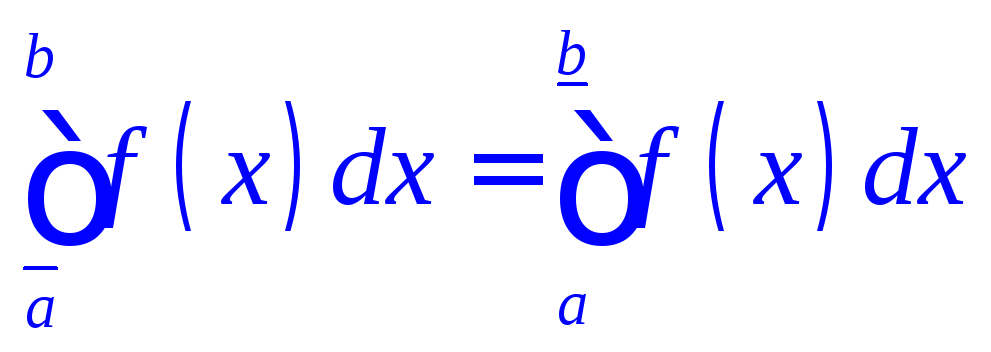 .
При
этом,
.
При
этом,
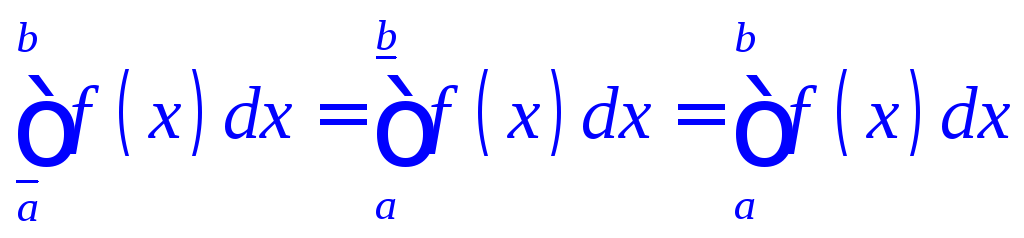 .
В соответствии с данным критерием под
интегралом Римана часто понимают общее
значение верхнего и нижнего интегралов.
.
В соответствии с данным критерием под
интегралом Римана часто понимают общее
значение верхнего и нижнего интегралов.
Следствие.
Любая
убывающая числовая последовательность
![]() имеет
имеет![]() ,
любая возрастающая числовая
последовательность
,
любая возрастающая числовая
последовательность![]() имеет
имеет
![]() .
.
Установим теперь свойство сохранения неравенств при предельном переходе.
Теорема
13.6. Пусть
![]() и
и![]() - две числовые сети, причем
- две числовые сети, причем![]() для всех
для всех![]() .
Если существуют
.
Если существуют![]() и
и![]() ,
то
,
то
![]() .
.
Доказательство
проведем от
противного. Пусть
![]() .
Возьмем произвольное число
.
Возьмем произвольное число![]() так, чтобы
так, чтобы![]() ,
и применим теорему 13.4. Тогда найдутся
такие индексы
,
и применим теорему 13.4. Тогда найдутся
такие индексы
![]() ,
что
,
что![]() для всех
для всех![]() и
и![]() для всех
для всех![]() .
Найдем индекс
.
Найдем индекс![]() так, чтобы
так, чтобы![]() и
и![]() .
Тогда
.
Тогда![]() ,
что противоречит условию теоремы.#
,
что противоречит условию теоремы.#
Следствие 1.
Пусть
![]() и
и![]() - числовые последовательности, причем
- числовые последовательности, причем![]() для всех номеров
для всех номеров![]() .
Если существуют
.
Если существуют![]() и
и![]() ,
то
,
то
![]() .
.
В качестве другого элементарного применения теоремы 13.6 приведем свойство монотонности интеграла Римана:
Следствие
2.
Пусть
функции
![]() интегрируемы по Риману и
интегрируемы по Риману и![]() для любого
для любого![]() .
Тогда
.
Тогда
![]() .
.
Отметим, что строгие неравенства при предельном переходе могут не сохраняться.
Следующее утверждение называется теоремой о пределе промежуточной переменной.
Теорема
13.7. Пусть
![]() ,
,![]() и
и![]() - такие числовые сети, что
- такие числовые сети, что![]() для любого
для любого![]() ,
и
,
и![]() .
Тогда существует
.
Тогда существует
![]() .
.
Доказательство.
Применяя определение предела к сетям
![]() и
и![]() ,
получим,
что для любого
,
получим,
что для любого
![]() найдется такой индекс
найдется такой индекс![]() ,
что
,
что![]() для всех
для всех![]() .
Из определений
.
Из определений![]() окрестностей
и неравенств
окрестностей
и неравенств
![]() следует, что
следует, что
![]() для всех
для всех![]() .
Это и означает, что
.
Это и означает, что
![]() .
#
.
#
Следствие.
Пусть
![]() ,
,![]() и
и![]() - числовые последовательности, причем
- числовые последовательности, причем![]() для всех номеров
для всех номеров![]() ,
и
,
и![]() .
Тогда существует
.
Тогда существует
![]() .
.
Пусть
![]() и
и![]() .
Из неравенств
.
Из неравенств![]() и
и![]() следует, что
следует, что
![]() ; (54)
; (54)
из неравенств
![]() ,
,![]() следует, что
следует, что![]() ,
откуда вытекает включение:
,
откуда вытекает включение:
![]() , (55)
, (55)
а из неравенств
![]() ,
,![]() ,
,![]() следует включение:
следует включение:
![]() . (56)
. (56)
Далее, если
![]() ,
то
,
то![]() и
и![]() ,
поэтому из неравенств
,
поэтому из неравенств
![]() ,
,![]() ,
,![]()
очевидно, получается включение:
![]() , (57)
, (57)
а из неравенств
![]() ,
,![]() ,
,![]()
вытекает включение:
![]() . (58)
. (58)
Соотношения (54) - (58) будут использованы ниже.
Следующее утверждение называется теоремой о пределе суммы:
Теорема
13.8.
Пусть
![]() и
и![]() - числовые сети,
- числовые сети,![]() и
и![]() .
Тогда
.
Тогда
![]() ,
(59)
,
(59)
если
операция
![]() определена в расширенной числовой
прямой.
определена в расширенной числовой
прямой.
Доказательство.
Пусть точки
![]() и
и![]() таковы, что сумма
таковы, что сумма![]() определена (см. (35)). Зададим
определена (см. (35)). Зададим![]() (если
(если![]() ,
а
,
а![]() или
или![]() ,
то будем считать, что
,
то будем считать, что![]() ).
По определению предела числовой сети
существует такой индекс
).
По определению предела числовой сети
существует такой индекс![]() ,
что
,
что![]() и
и![]() для всех
для всех![]() .
Для указанных значений индексов
.
Для указанных значений индексов![]() из соотношений (54) - (58) вытекает, что
из соотношений (54) - (58) вытекает, что![]() .
#
.
#
Замечание. 1) Из доказанной теоремы, в частности, следует, что
![]() , (60)
, (60)
т.е. производная суммы двух функций равна сумме их производных, и
![]() , (61)
, (61)
т.е. интеграл Римана от суммы двух функций равен сумме их интегралов, если суммы в правых частях равенств (60) и (61) определены.
2) Если
![]() для любого индекса
для любого индекса![]() и
и![]() ,
то
,
то![]() ,
поэтому из теоремы 13.8 следует, что
,
поэтому из теоремы 13.8 следует, что
![]() , (62)
, (62)
где операция сложения в правой части равенства (62) осуществляется в соответствии с формулами (31) - (32). Исходя из формулы (62), часто говорят, что «константу можно выносить из-под знака предела».
Следующее утверждение называется теоремой о пределе произведения:
Теорема
13.9. Пусть
![]() и
и![]() - числовые сети,
- числовые сети,![]() и
и![]() .
Тогда
.
Тогда
![]() ,
(63)
,
(63)
если
операция
![]() определена.
определена.
Доказательство.
Зададим
![]() и рассмотрим различные варианты значений
и рассмотрим различные варианты значений![]() и
и![]() .
.
Пусть
![]() .
Выберем число
.
Выберем число![]() так, чтобы
так, чтобы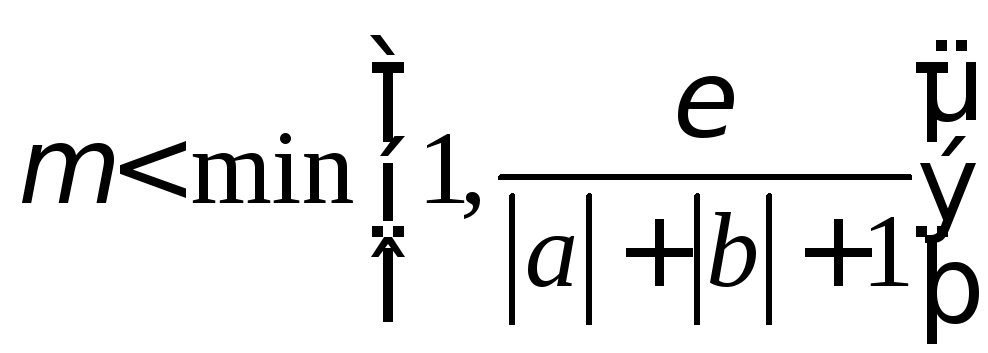 ,
и найдем такой индекс
,
и найдем такой индекс![]() ,
что
,
что![]() ,
а
,
а![]() для всех
для всех![]() .
Тогда из неравенств
.
Тогда из неравенств![]() ,
,![]() и
и
![]()
следует, что
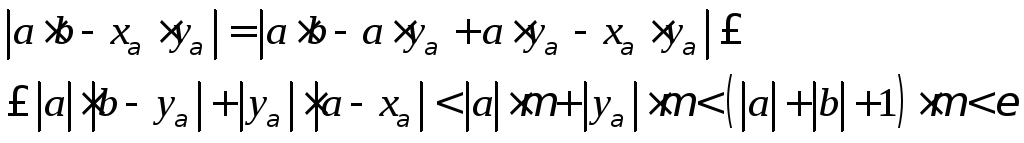
для всех
![]() ,
т.е.
,
т.е.![]() при
при![]() .
Это доказывает формулу (63).
.
Это доказывает формулу (63).
Пусть
![]() ,
,![]() .
Выберем
.
Выберем![]() так, чтобы
так, чтобы![]() .
Тогда по определениям пределов сетей
найдется такой индекс
.
Тогда по определениям пределов сетей
найдется такой индекс![]() ,
что
,
что![]() и
и![]() для всех
для всех![]() .
Теперь из неравенства
.
Теперь из неравенства![]() следует, что
следует, что![]() для всех
для всех![]() ,
так что
,
так что![]() .
.
Если
![]() ,
,![]() ,
то для
,
то для![]() найдется такой индекс
найдется такой индекс![]() ,
что
,
что![]() и
и![]() для всех
для всех![]() .
Тогда
.
Тогда![]() и поэтому
и поэтому![]() .
Следовательно,
.
Следовательно,![]() для всех
для всех![]() ,
т.е.
,
т.е.![]() .
.
Пусть теперь
![]() ,
,![]() .
Для любого
.
Для любого![]() найдем индекс
найдем индекс![]() так, чтобы
так, чтобы![]() и
и![]() для всех
для всех![]() .
Тогда
.
Тогда![]() при
при![]() ,
так что
,
так что![]() .
.
Если
![]() ,
,![]() ,
то для любого
,
то для любого![]() найдется такое
найдется такое![]() ,
что
,
что![]() и
и![]() для всех
для всех![]() .
Тогда
.
Тогда![]() ,
а
,
а![]() для всех
для всех![]() ,
так что
,
так что![]() .
.
Все оставшиеся
варианты значений точек
![]() и
и![]() легко сводятся к рассмотренным выше.#
легко сводятся к рассмотренным выше.#
Замечание.
Из теоремы
13.9 следует, что для
любого
![]()
![]() , (64)
, (64)
если
правая часть равенства (64) определена
(она не определена, когда
![]() и
и![]() ).
Отметим, что умножение справа в равенстве
(64) осуществляется в соответствии с
правилами (33) – (34). Исходя из формулы
(64), часто говорят, что “постоянный
множитель можно выносить из-под знака
предела”.
).
Отметим, что умножение справа в равенстве
(64) осуществляется в соответствии с
правилами (33) – (34). Исходя из формулы
(64), часто говорят, что “постоянный
множитель можно выносить из-под знака
предела”.
Замечание.
Теоремы
13.8 и 13.9 можно доказать и для любого
конечного числа числовых сетей.
При этом следует лишь избегать появления
“запрещеных” операций:
![]() ,
,![]() и
и![]() .
.
Числовую
сеть
![]() будем называть
локально
ограниченной,
если
существует такое число
будем называть
локально
ограниченной,
если
существует такое число
![]() и индекс
и индекс![]() ,
что
,
что![]() для всех индексов
для всех индексов
![]() .
Нетрудно заметить, чтодля
числовой последовательности понятие
локальной ограниченности совпадает с
хорошо известным понятием
ограниченной последовательности:
последовательность
.
Нетрудно заметить, чтодля
числовой последовательности понятие
локальной ограниченности совпадает с
хорошо известным понятием
ограниченной последовательности:
последовательность
![]() называется
ограниченной,
если
существует такое число
называется
ограниченной,
если
существует такое число
![]() ,
что
,
что![]() для всех номеров
для всех номеров
![]() .
Применительно к числовым сетям,
построенным по функциям (см. примеры
12.2, 12.3 и 12.4), это понятие приводит к
известному из курса математического
анализа определению локально ограниченной
функции:функция
.
Применительно к числовым сетям,
построенным по функциям (см. примеры
12.2, 12.3 и 12.4), это понятие приводит к
известному из курса математического
анализа определению локально ограниченной
функции:функция
![]() называется
локально
ограниченной в предельной точке
называется
локально
ограниченной в предельной точке
![]() множества
множества
![]() ,если
существуют такие числа
,если
существуют такие числа
![]() и
и![]() ,
что
,
что![]() для всех
для всех![]() ,
,
![]() .
Отметим, что, как следует из определения
предела числовой сети,всякая
числовая сеть, имеющая конечный предел,
является локально ограниченной.
В соответствии с распространенными в
математике традициями числовую
сеть
.
Отметим, что, как следует из определения
предела числовой сети,всякая
числовая сеть, имеющая конечный предел,
является локально ограниченной.
В соответствии с распространенными в
математике традициями числовую
сеть
![]() будем называть
бесконечно
малой,
если
она имеет предел и
будем называть
бесконечно
малой,
если
она имеет предел и
![]() .
Имеет место
.
Имеет место
Теорема
13.10. Произведение
бесконечно малой числовой сети
![]() на локально ограниченную числовую сеть
на локально ограниченную числовую сеть![]() является бесконечно малой числовой
сетью.
является бесконечно малой числовой
сетью.
Доказательство.
Пусть число
![]() и индекс
и индекс![]() таковы, что
таковы, что![]() для всех индексов
для всех индексов![]() .
Возьмем
.
Возьмем![]() и найдем индекс
и найдем индекс![]() так, чтобы
так, чтобы![]() для всех индексов
для всех индексов![]() .
Выберем теперь индекс
.
Выберем теперь индекс![]() так, чтобы
так, чтобы![]() и
и![]() .
Тогда для всех индексов
.
Тогда для всех индексов![]() выполняется неравенство
выполняется неравенство![]() ,
которое и означает, что
,
которое и означает, что
![]() .
#
.
#
В заключение параграфа приведем теорему о пределе частного.
Теорема
13.11. Пусть
![]() и
и![]() - числовые сети,
- числовые сети,![]() и
и![]() .
Тогда
.
Тогда
![]() , (65)
, (65)
если
операция
![]() определена.
определена.
Доказательство.
Предположим сначала, что
![]() и
и
![]() .
По определению предела числовой сети
найдется такой индекс
.
По определению предела числовой сети
найдется такой индекс![]() ,
что неравенство
,
что неравенство![]() будет выполняться для всех индексов
будет выполняться для всех индексов![]() .
Для указанных индексов
.
Для указанных индексов![]() выполняется:
выполняется:
![]() . (66)
. (66)
Положим
![]() ,
,![]() и для любого числа
и для любого числа![]() в соответствии с определениями пределов
найдем такие индексы
в соответствии с определениями пределов
найдем такие индексы![]() и
и![]() ,
что
,
что![]() для всех
для всех![]() ,
и
,
и![]() для всех
для всех![]() .
Выберем индекс
.
Выберем индекс![]() так, чтобы
так, чтобы![]() ,
,![]() и
и![]() .
Используя неравенства (66), теперь для
всех индексов
.
Используя неравенства (66), теперь для
всех индексов![]() ,
имеем:
,
имеем:
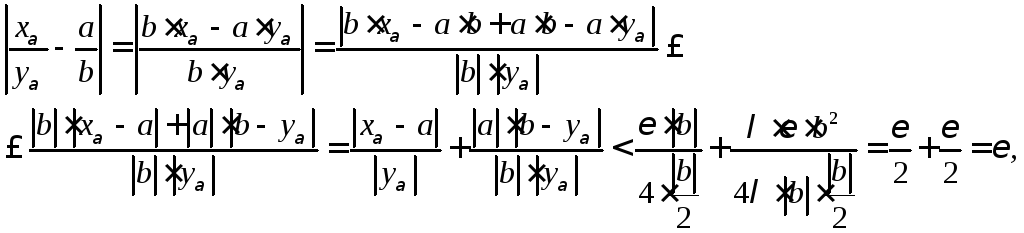
что и доказывает формулу (65).
Пусть теперь
![]() ,
,![]() ,
,![]() .
Для любого числа
.
Для любого числа![]() по определениям пределов числовых сетей
найдется такой индекс
по определениям пределов числовых сетей
найдется такой индекс![]() ,
что
,
что![]() и
и![]() для всех индексов
для всех индексов![]() .
Тогда
.
Тогда![]() для всех
для всех![]() и, значит, для всех таких индексов
выполняется неравенство
и, значит, для всех таких индексов
выполняется неравенство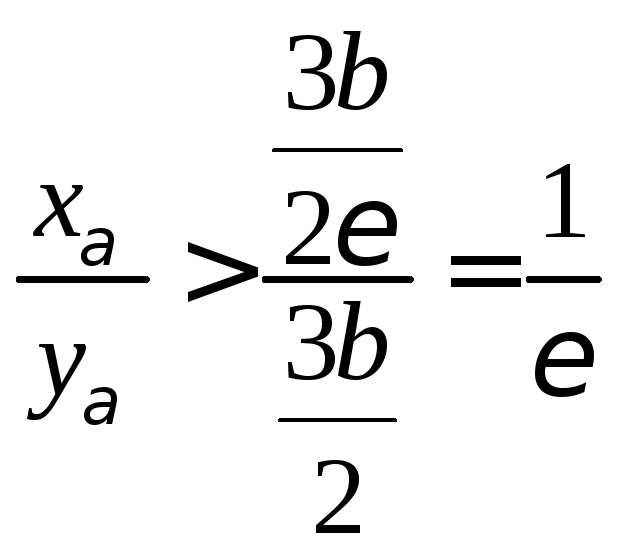 ,
что вновь доказывает формулу (65).
,
что вновь доказывает формулу (65).
Случаи
![]() ,
,![]() ,
а также
,
а также![]() ,
,![]() и
и![]() ,
,![]() доказываются аналогично.
доказываются аналогично.
Предположим,
наконец, что
![]() ,
,![]() .
Возьмем число
.
Возьмем число![]() и найдем такой индекс
и найдем такой индекс![]() ,
что
,
что![]() и
и![]() для всех индексов
для всех индексов![]() .
Тогда
.
Тогда![]() и поэтому
и поэтому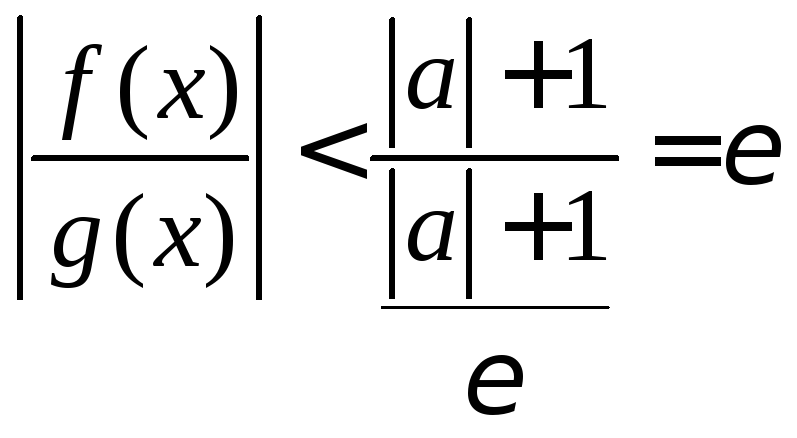 для всех
для всех![]() .
Тем самым, вновь установлена формула
(65).
.
Тем самым, вновь установлена формула
(65).
Случай
![]() ,
,![]() доказывается аналогично. #
доказывается аналогично. #
Рассмотрим теперь вопрос о “делении на нуль”.
Теорема
13.12. Пусть
![]() и
и![]() - числовые сети,
- числовые сети,![]() ,
причем
,
причем![]() ,
,![]() .
Тогда:
.
Тогда:
если существует такой индекс
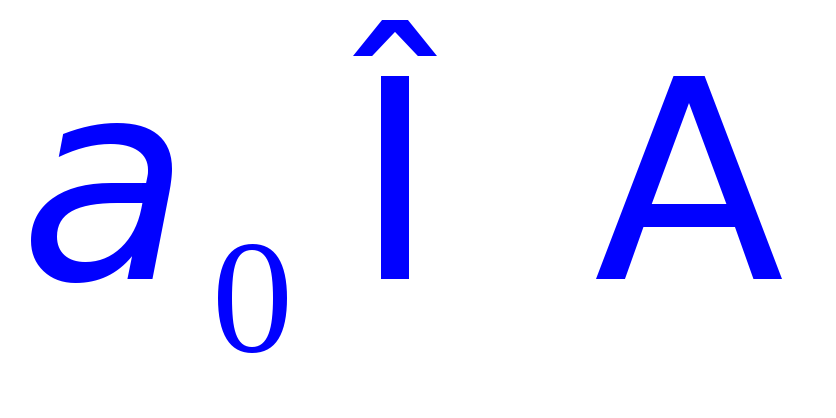 ,
что
,
что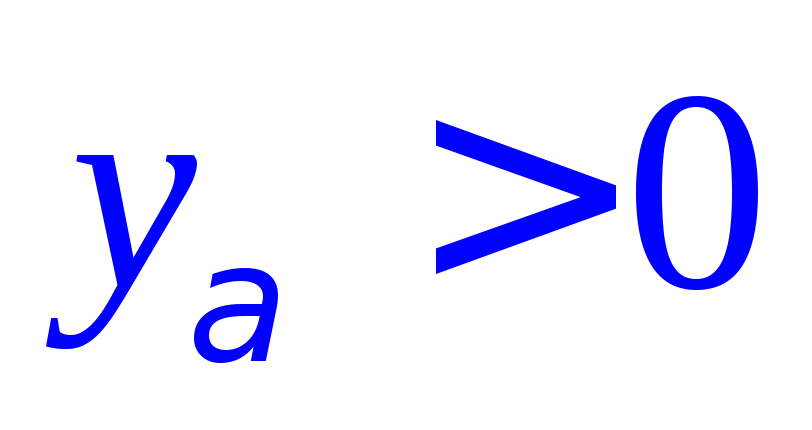 для всех индексов
для всех индексов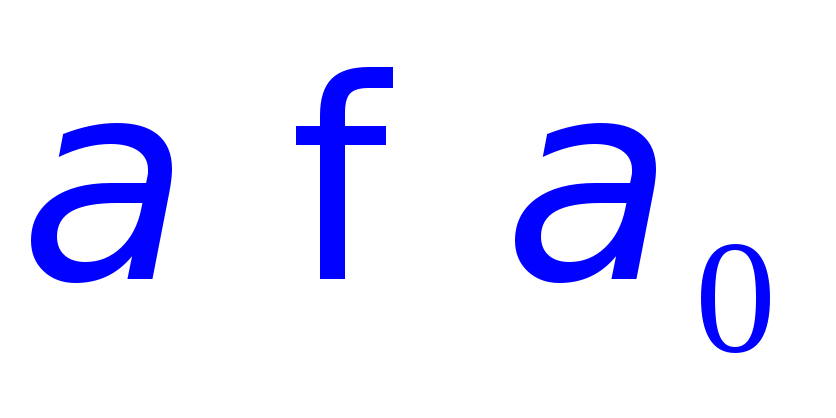 ,
то
,
то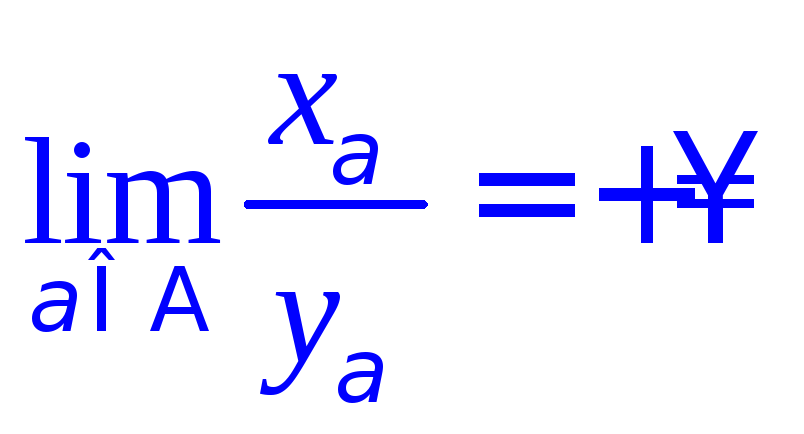 ,
если
,
если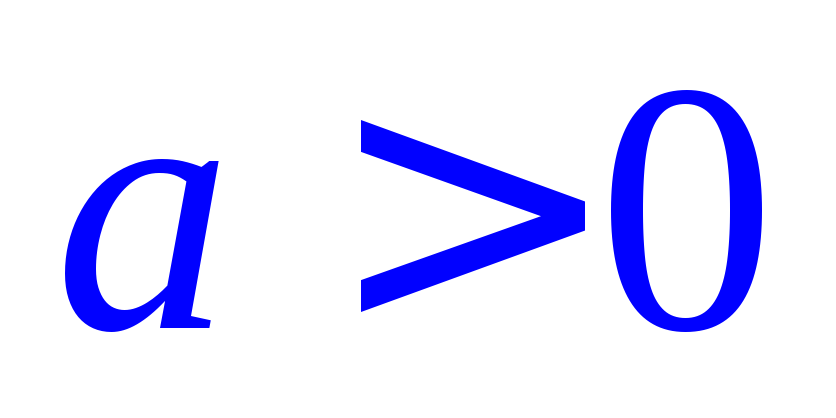 ,
и
,
и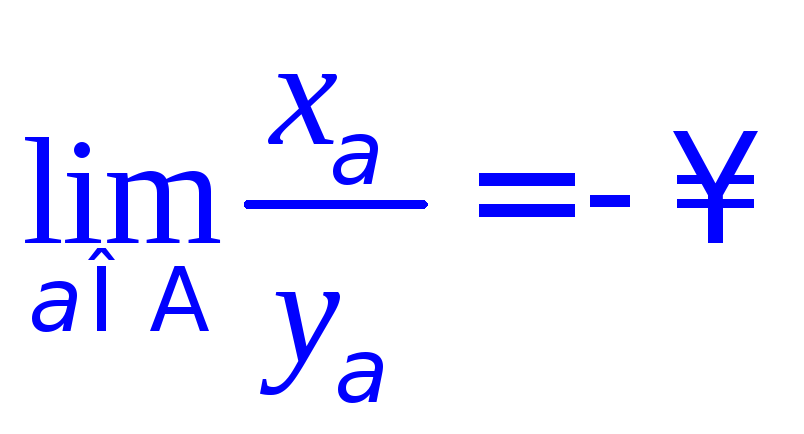 ,
если
,
если
 ;
;если существует такой индекс
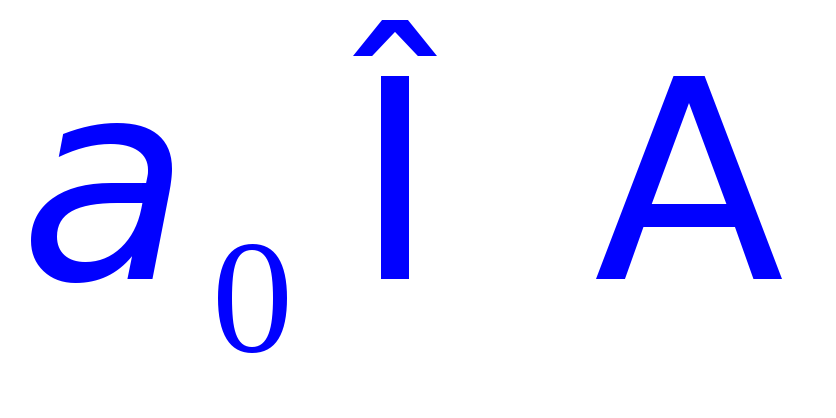 ,
что
,
что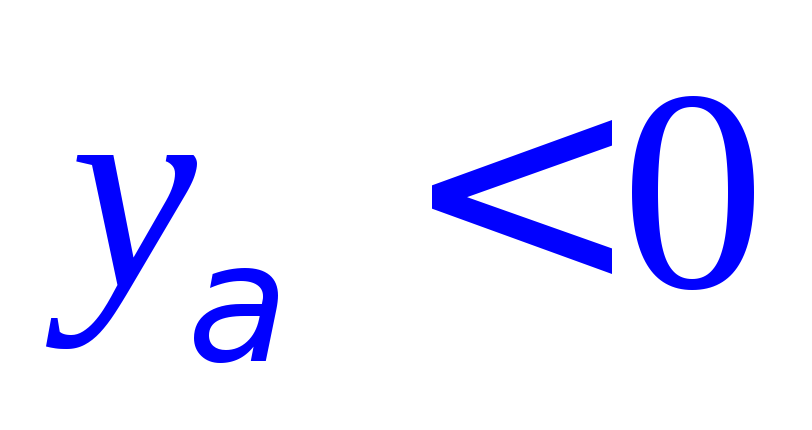 для всех индексов
для всех индексов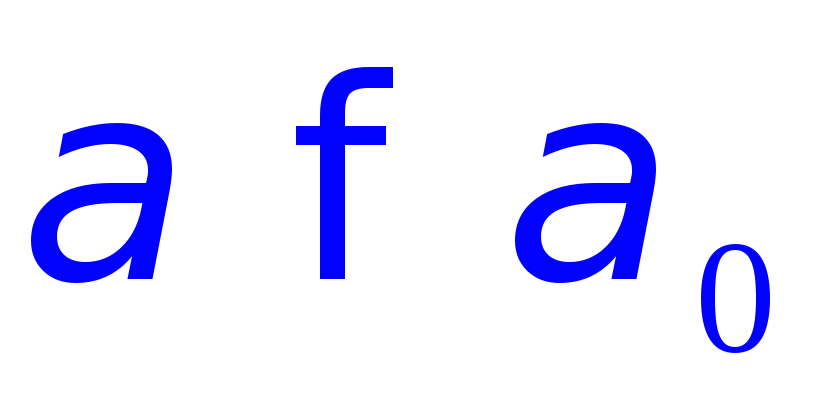 ,
то
,
то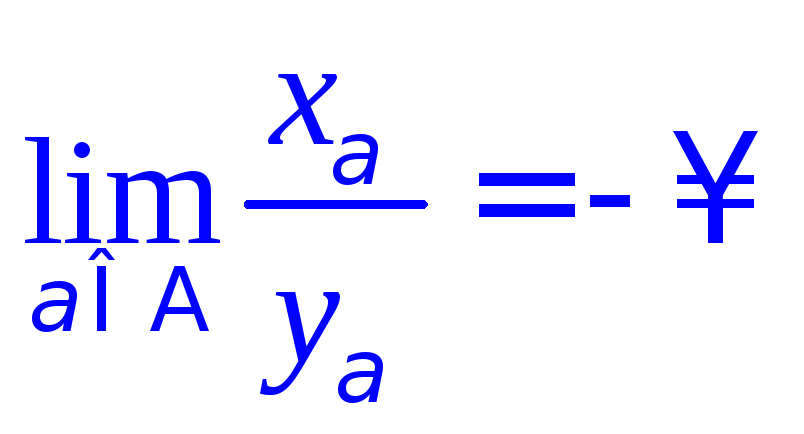 если
если ,
и
,
и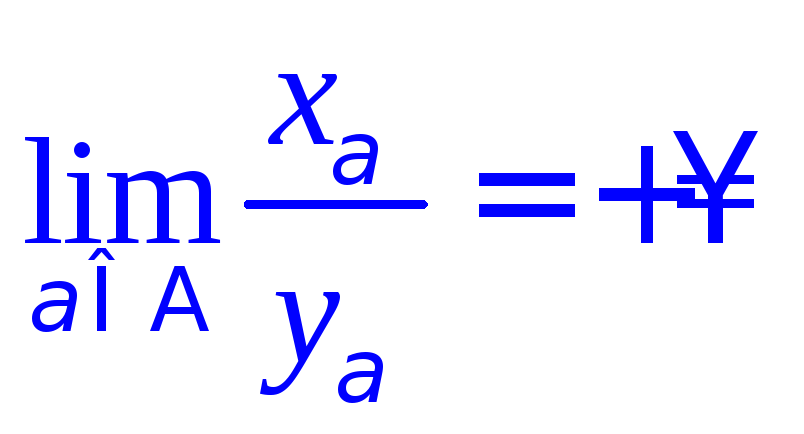 ,
если
,
если
 .
.
Доказательство.
Пусть
![]() и
и![]() для всех
для всех![]() .
По определению предела для любого числа
.
По определению предела для любого числа![]() найдется такой индекс
найдется такой индекс![]() ,
что
,
что![]() и
и![]() для всех
для всех![]() .
Возьмем индекс
.
Возьмем индекс![]() так, чтобы
так, чтобы![]() и
и![]() .
Тогда для всех индексов
.
Тогда для всех индексов![]() будет
будет![]() и
и![]() ,
откуда
,
откуда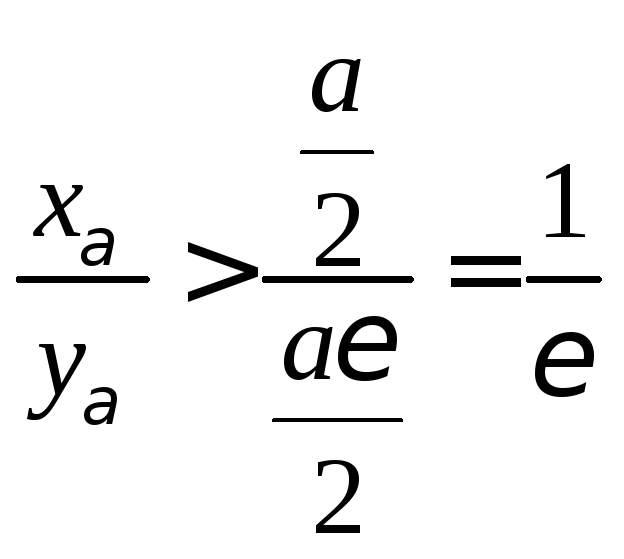 ,
так что
,
так что
![]() .
Остальные случаи доказываются аналогично.
#
.
Остальные случаи доказываются аналогично.
#
В заключение приведем наиболее часто встречающийся случай применения данного результата, относящийся к вычислению пределов функций:
Следствие.
Пусть
![]() - некоторые функции,
- некоторые функции,![]() - предельная точка множества
- предельная точка множества![]() ,
,![]() ,
причем
,
причем![]() ,
,![]() .
Тогда:
.
Тогда:
1) если
существует такое
![]() ,
что
,
что![]() для всех
для всех![]()
![]() ,
то
,
то![]() если
если![]() ,
и
,
и![]()
![]() если
если
![]() ;
;
2) если
существует такое
![]() ,
что
,
что![]() для всех
для всех![]()
![]() ,
то
,
то![]() если
если![]() ,
и
,
и![]() если
если
![]()
![]()
Упражнения. 1) Пользуясь определением предела доказать, что:
а)
![]() ;
б)
;
б)![]() в)
в)![]() ;
;
г)
![]() ;
д)
;
д)![]() ;
е)
;
е)![]() ;
;
ж)
![]() ;
з)
;
з)![]() ;
и)
;
и)![]() ;
к)
;
к)![]() .
.
