будем называть окрестностью точки и обозначать . Изменяя действительные числа , мы будем изменять иокрестности точки , поэтому каждая точка обладает большим запасомокрестностей (мощность множества всехокрестностей точкиравна континууму, так как эту мощность имеет множество всех положительных действительных чисел).Введем теперь определения окрестностей для точек и :

, . (38)

Мотивацию таких определений проясняет стереографическая проекция:

Из рисунка видно, что интервал на числовой прямой (закрашенкрасным цветом) отображается в интервал на окружности, внутри которого находится точка . Для точкине существует на окружности интервалов, внутри которых находится эта точка, поскольку окружность разрезана (точкаможет быть лишь концевой точкой полуинтервалов). Поэтому в качествеокрестности точкиприходится выбирать полуинтервал, расположенный на окружности справа от(закрашен синим цветом), а в качествеокрестности точкивыбирают полуинтервал, расположенный на окружности слева от.

Таким образом,

Отметим важное соотношение для окрестностей любой точки:если , то .

Докажем теперь лемму, устанавливающую свойство отделимости расширенной числовой прямой (это свойство также называют свойством Хаусдорфа).

Лемма 10.1. Для любых двух различных точек ирасширенной числовой прямой существуют такие ихокрестностии, что

. (39)

Доказательство. Если , а, то равенство (39) выполняется для любого(см. формулы (38)). Пусть теперь, аили. Выберем любое числотак, чтобы. Тогдаи

,

откуда и следует соотношение (39) сразу для и. Наконец, если и, например, , то длявыполняется равенство:, откуда вновь вытекает соотношение (39). #

Рассмотрим некоторое непустое множество . По отношению квсе точки делятся на два типа: точка называется точкой прикосновения для множества , еслидля любого (т.е. если каждаяокрестность точкипересекается с);точка называется внешней точкой множества , если существует такое, что (т.е. если некотораяокрестность точкине пересекается с множеством).

Совокупность всех точек прикосновения множества обозначим через . Поскольку каждая точка множества является его точкой прикосновения, товсегда . При этом множество может, как совпадать с, так и быть его собственным подмножеством. Например, для множеств,имеем:.

Точки прикосновения также делятся на два типа. Точка называется изолированной точкой множества , если существует такое, что , т.е. если пересечение некоторой окрестности точкис множествомсостоит лишь из одной точки. Остальные точки множестваназываются его предельными точками. Итак, точка называется предельной точкой множества , еслидля любого , т.е.если каждая окрестность точкив пересечении с множествомимеет точки, отличные от . Легко понять, что множество должно содержать бесконечно много точек множества .

Пример 10.1. 1) Пусть , где. Тогда имеем:. Предельные точки множествасоставляют множество, а точка- изолированная точка множества.

2) Рассмотрим множество всех натуральных чисел . Все точки множества будут его изолированными точками, а точка является предельной точкой множества.

3) У множества целых чисел есть две предельные точки: и, а изолированными являются все точки множества.

4) Множество рациональных чисел не имеет изолированных точек. Все точки расширенной числовой прямой являются предельными точками множества (это немедленно вытекает из теоремы 8.1).

5) Множество иррациональных чисел не имеет изолированных точек. Из теоремы 8.1 следует, что все точки расширенной числовой прямой являются предельными точками этого множества.

Пример 10.2. Доказать, что является предельной точкой последовательности.

Решение. Для любого натурального числа обозначим. Согласно определению предельной точки для любогонеобходимо указать такой номер, что. Для нахождения требуемого номера рассмотрим цепочку неравенств

,

справедливых для любого номера . Решая последнее неравенство, получаем. Следовательно, можно взять,где обозначает целую часть числа . #

Теперь выясним, каким множествам гарантировано наличие предельных точек?

Лемма 10.2. Любое конечное множество состоит только из изолированных точек.

Доказательство. Пусть множество является конечным и.

Если , то,или. Во всех этих трех случаях множествосостоит лишь из изолированных точек.

Предположим теперь, что . Поскольку множествоконечное, то его можно представить в виде. Пусть. Тогдаилидля числа, поэтомуявляется изолированной или внешней точкой множества(первый вариант соответствует случаю, когда, а второй – случаю, когда). Аналогичный вывод можно сделать и для точки.

Рассмотрим теперь точку . Так какни для какого, тоиСледовательно, все точки множестваявляются внешними для.

Таким образом, все точки прикосновения множества лежат в. Пусть. Тогдадля некоторого. Положим. Тогдаи, так что точка- изолированная точка множества. #

Итак, предельные точки бывают только у бесконечных множеств. Но все ли бесконечные множества их имеют? Ответ на поставленный вопрос дает следующая теорема Больцано-Вейерштрасса, для доказательства которой потребуются новые понятия. Множество называется ограниченным снизу в , если существует такое число , чтодля любого .Множество называется ограниченным сверху в , если существует такое число , чтодля любой точки .Множество, одновременно ограниченное и снизу и сверху в , называется ограниченным в . Отметим, что любое множество является ограниченным в .

Теперь можно доказать теорему Больцано-Вейерштрасса:

Теорема 10.1. Любое бесконечное множество имеет хотя бы одну предельную точку.

Доказательство. Предположим сначала, что множество не является ограниченным сверхув . Тогда для любого действительного числа найдется точкатакая, что. Так каки, то это означает, чтоявляется предельной точкой множества, а значит и предельной точкой множества. Аналогичным образом устанавливается, чтоявляется предельной точкой множества, если множествоне является ограниченным снизув .

Предположим теперь, что множество ограниченов . Тогда найдутся такие действительные числа и, чтоидля всех. Разобьем отрезокпополам точкойи из двух отрезковивыберем тот, в котором содержится бесконечно много точек множества. Такой отрезок обязательно найдется, иначе множествоокажется конечным. Если оба отрезкаисодержат бесконечно много точек множества, то выберем любой из них. Выбранный отрезок обозначим через, разобьем его пополам и из двух вновь полученных отрезков выберем тот, который содержит бесконечно много точек множества. Выбранный отрезок обозначим через. Описанную процедуру деления отрезков пополам и выбора новых отрезков продолжим и дальше. В итоге мы получим последовательность вложенных отрезков, каждый из которых содержит бесконечно много точек множества. По аксиоме Кантора существует точка, общая для всех этих отрезков. Покажем, что- предельная точка множества. Зададими выберем номер так, чтобы (для этого числоможно представить в виде десятичной дробии положить; тогда). Так как длина отрезкаравна, а, то, откуда,и, следовательно,

.

Эти неравенства означают, что Таким образом, любаяокрестность точкисодержит бесконечно много точек множества, т.е.- это предельная точка множества, а значит, и. #

Приведем дальнейшую классификацию предельных точек множеств. Точку будем называть предельной слева точкой множества ,если каждая окрестность точкисодержит точкутакую, что . Соответственно,точку назовем предельной справа точкой множества ,если каждая окрестность точкисодержит точкутакую, что . Очевидно,точка может быть только предельной справа, а точка - только предельной слева точкой множества .

Разумеется, могут существовать и такие точки, которые будут одновременно предельными слева и справа. Например, если , то точки множестваявляются предельными слева точками множества, точки множества- предельными справа точками множества, а точки множествабудут дляодновременно предельными слева и справа.

Предельные слева и предельные справа точки множества являются предельными точками этого множества, так что они лежат в . Обратное утверждение также верно:

Лемма 10.3. Если - предельная точка множества, тодолжна быть предельной слева или предельной справа точкой этого множества.

Доказательство. Если предположить противное, то и поэтому найдутся такие, чтои. Пусть. Тогдаи, поэтому либо, либо. В первом случаебудет внешней точкой множества, а во втором - изолированной точкой множества. #

Пример 10.3. Доказать, что число 3 является предельной слева, но не справа, точкой последовательности .

Решение. Поскольку для любого номера

,

то число 3 не может быть предельной справа точкой заданной последовательности.

Возьмем теперь некоторое действительное число и будем искать номертак, чтобы. Решая для этого неравенство, получим, так что можно взять. Следовательно, для любогонайдется такой номер, что. Это означает, что число 3 является предельной слева точкой данной последовательности.#

Упражнения. 1) Доказать, что является предельной точкой последовательности.

2) Доказать, что является предельной точкой последовательности.

3) Доказать, что 0 является предельной справа, но не слева, точкой последовательности .

4) Доказать, что 2 является предельной слева, но не справа, точкой последовательности .

5) Доказать, что является предельной справа, но не слева, точкой последовательности.

6) Доказать, что 2 является предельной и слева и справа точкой последовательности .

7) Доказать, что 1 является предельной и слева и справа точкой последовательности .

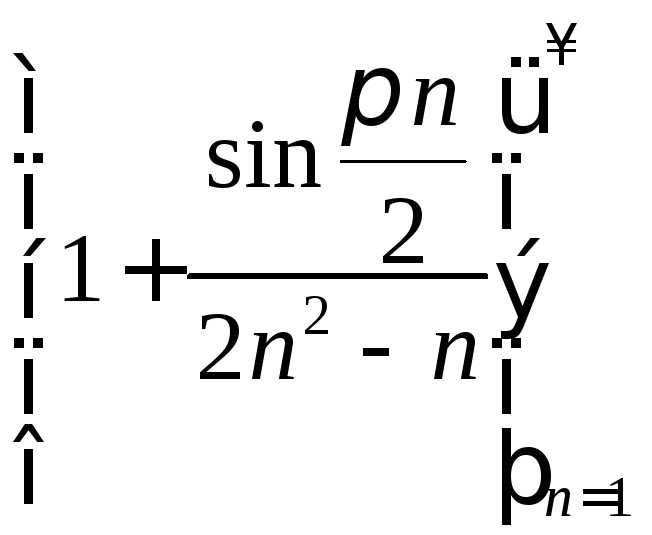11. Грани множеств в расширенной числовой прямой

Пусть - некоторое множество в расширенной числовой прямой .Каждая точка такая, чтодля любого, называется верхней границей множества , а каждая точка такая, чтодля любого, называется нижней границей множества . Разумеется,точка является нижней границей, а- верхней границей любого множества . Среди всех верхних границ множестваособый интерес представляетнаименьшая верхняя граница, которая называется верхней гранью множества и обозначается (от латинского словаsupremum). Соответственно, среди всех нижних границ множества выделяетсянаибольшая нижняя граница множества , котораяназывается нижней гранью множества и обозначается (infimum ).Для верхних и нижних граней используются также обозначения и. Отметим, чтоесли множество является ограниченным снизу в , то его нижняя грань будет действительным числом. Аналогичным образом можно утверждать, что если множество является ограниченным сверху в, то его верхняя грань будет действительным числом.

Пример 11.1. 1) Если или, где, то,.

2) Если , то,.

3) Если , то,.

Большое число новых примеров доставляет следующая

Лемма 11.1. Если - наибольший элемент множества, то .Если - наименьший элемент множества, то.

Доказательство. Пусть - наибольший элемент множества . Так какдля любого, то- верхняя граница множества. Если - некоторая верхняя граница множества , то, так как.Следовательно,. Равенстводоказывается аналогично. #

Для нахождения верхних и нижних граней часто весьма удобной бывает следующий критерий граней:

Теорема 11.1. 1) Пусть - нижняя граница множества .Для того чтобы точка была нижней гранью множества, необходимо и достаточно, чтобыбыла точкой прикосновения для . 2)Пусть - верхняя граница множества .Для того чтобы точка была верхней гранью множества, необходимо и достаточно, чтобыбыла точкой прикосновения для .

Доказательство. Докажем только первое утверждение. Пусть - нижняя граница множества. Обе части утверждения будем доказывать методом от противного.

Необходимость. Пусть , ноне является точкой прикосновения для множества. Тогдабудет внешней точкой множества, поэтому существует такое, что. Отсюда следует, что(если) или(если) для всех точек. В любом случае существует нижняя граница множества, которая будет больше, чем(в первом случае ею будет, например, точка, а во втором – точка). Следовательно,.

Достаточность. Пусть является точкой прикосновения для множества, но. Поскольку - это нижняя граница, то существует нижняя границамножестватакая, что. По свойству Хаусдорфа (см. лемму 10.1) существует такое, что. Из определенияокрестностей (см. (37), (38)) и неравенстваследует, чтодля всех точеки всех. Следовательно,, так чтоне является точкой прикосновения для множества. Полученное противоречие и завершает доказательство теоремы. #

Замечание. Обычно под критерием граней понимается характеризация верхних и нижних граней ограниченных множеств . В этом случае из теоремы 11.1 очевидно вытекает

Следствие. 1) Пусть - нижняя граница множества . Число является нижней гранью множества тогда и только тогда, когда для любого существует точка такая, что .

2) Пусть - верхняя граница множества . Число является верхней гранью множества тогда и только тогда, когда для любого найдется точка такая, что .

Установим теперь основной результат этого параграфа - теорему о существовании верхней и нижней грани любого множества в расширенной числовой прямой.

Теорема 11.2. Любое непустое множество имеет верхнюю и нижнюю грань.

Доказательство. Ограничимся лишь доказательством существования верхней грани.

Если , то по лемме 11.1.

Если и множествоне ограничено сверху в, то, как доказано в теореме 10.1,является предельной точкой множества. Следовательно, по теореме 11.1.

Предположим теперь, что множество ограничено сверху в. Если, тои утверждение доказано. Поэтому можно считать, что. Выберем из множествалюбую точкуи возмем произвольную верхнюю границу так, чтобы выполнялось следующее условие: в отрезке есть хотя бы одна точка множества (т.е.),а правее точки нет точек множества (т.е. нет таких точек, для которых выполняется неравенство). Далее разделим отрезокпополам точкой и выберем ту его половину, обозначим ее через , которая удовлетворяет требованию:в отрезке есть хотя бы одна точка множества, а правее этого отрезка нет точек множества . Заметим, чтотакой отрезок всегда существует и единственен. Вновь разделим отрезок пополам и выберем ту его половину, обозначим ее, которая удовлетворяет требованию:в отрезке есть хотя бы одна точка множества, а правее этого отрезка нет точек множества . Описанную процедуру продолжим и дальше. В результате получим последовательность вложенных отрезковПо аксиоме Кантора все эти отрезки имеют общую точку. Покажем, что.

Сначала установим, что является верхней границей множества. Доказательство проведем от противного. Пустьне является верхней границей. Тогда существует такая точка, что. Положими, как и при доказательстве теоремы 10.1, найдем такой номер, что. Так как длина отрезкаравна, а, то, откуда

,

что противоречит выбору отрезка (правее отрезкаесть точка). Полученное противоречие и доказывает, что- это верхняя граница множества.

Докажем теперь, что является наименьшей среди всех верхних границ множества. Предположим противное. Тогда существует такая верхняя границамножества, что. Положими, как и выше, найдем такой номер, что. Тогда, откуда следует, что в отрезкенет точек из множества. Полученное противоречие и завершает доказательство. #

Приведем теперь основные свойства верхних и нижних граней.

Теорема 11.3. Для любого множества справедливы формулы:

,. (40)

Доказательство. Проверим первое равенство. Пусть . Покажем, что. Действительно,идля всех. Следовательно,- это нижняя граница множества. Пусть теперь- некоторая нижняя граница множества. Тогдаидля любого, так что- верхняя граница множества. Поэтомуи. Следовательно,, и первая формула в (40) доказана. Для доказательства второго равенства, очевидно, достаточно применить первую формулу в (40) к множеству. #

Пусть . Введемсумму и произведение множеств и , а также произведение действительного числа на множество :

,,. (41)

Пример 11.2. Пусть ,. Тогда,. #

Замечание. Такие же операции, конечно, можно ввести для множеств и чисел; однако вводить их следует с особой осторожностью, так как при этом могут возникнуть запрещенные операции,и. Если для конкретных множестви чиселони не возникают, то сумма и произведения и вводятся по формулам (41).

Теорема 11.4. Для любых множеств справедливы формулы:

,. (42)

Доказательство. Проверим сначала первое равенство. Пусть и. Тогдадля всехи, так что- верхняя граница множества. Возьмем некоторую верхнюю границумножества. Тогдадля всехи. Зафиксируем некоторую точку. Тогдадля любого, так что. Отсюда получаем, чтодля любого, так как точкабыла взята произвольно из множества. Следовательно,, т.е.. Это означает, что, и первая формула в (42) доказана.

Для доказательства второго равенства применим к первому равенству в (42) формулы (41):

. #

Если и , то операции , иопределены, причем, поэтому имеет место следующее дополнение к теореме 11.4:

Теорема 11.5. Пусть и. Тогда

, .

Теорема 11.6. Пусть и .Тогда:

,. (43)

Доказательство. Пусть . Тогдаи, значит,для любого. Следовательно,- верхняя граница множества. Пусть- какая-то верхняя граница множества. Тогдаидля всех, так что. Следовательно,, т.е.. Тем самым доказана первая формула в (43). Докажем теперь вторую формулу в (43):

. #

Следствие. Пусть и .Тогда:

,.

Доказательство. Проверим только первое равенство:

. #

Теорема 11.7. Пусть .

1) Если для любой точки существует такая точка, что , то . 2)Если для любой точки существует такая точка ,что ,то .

Доказательство. Докажем только первое утверждение. Пусть и. По условию теоремы для любой точкисуществует точка, такая что. Но, поэтому и. Итак,является верхней границей для множества, поэтому. #

Условия теоремы 11.7 выполнены, например, в случае, когда , поэтому выполняется

Следствие. Пусть .Тогда и .

Теорема 11.8. Пусть .Тогда и .

Доказательство. Докажем сначала первую формулу. Пусть для любогои. Тогда по предыдущему следствиюдля любого, поэтому. Пусть теперь. Тогда существует такое, что, поэтому. Но тогда, так что. Вторую формулу можно доказать, опираясь на формулы (40):

. #

Упражнения. Найти и, где:

1) ; 2); 3) ; 4); 5); 6).