1. 2. Операции с числами |
16 |
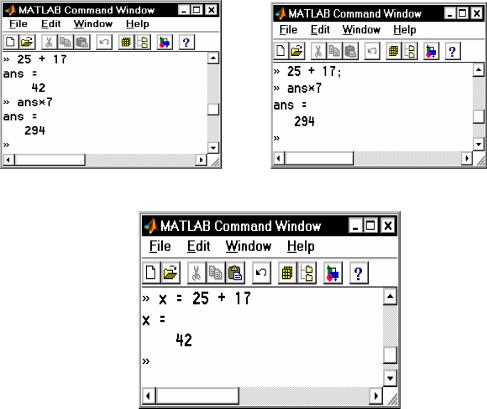
символом ' ; ', после нажатия клавиши <Enter> в командном окне возникнет результат выполнения в виде :
<Имя переменной> = <результат>.
|
|
|
|
|
Рис. 1.7 |
|
Рис. 1.8 |
||
|
|
|
|
|
|
|
|
|
|
Рис. 1.9
Например, если ввести в командное окно строку 'x = 25 + 17', на экране появится запись (рис. 1.9) :
Система MatLAB имеет несколько имен переменных, которые используются самой системой и входят в состав зарезервированных:
i, j - мнимая единица (корень квадратный из -1); pi - число π (сохраняется в виде 3.141592653589793); inf - обозначение машинной бесконечности; Na- обозначение неопределенного результата (например, типа 0/0 или inf/inf); eps - погрешность операций над числами с плавающей запятой; ans- результат последней операции без знака присваивания; realmax и realmin – максимально и минимально возможные величины числа, которое может быть использованы.
Эти переменные можно использовать в математических выражениях.
1.2.3. Ввод комплексных чисел
Язык системы MatLAB, в отличие от многих языков программирования высокого уровня, содержит в себе очень простую в пользовании встроенную арифметику комплексных чисел. Большинство элементарных математических функций допускают в качестве аргументов комплексные числа, а результаты формируются
1. 2. Операции с числами |
17 |
как комплексные числа. Эта особенность языка делает его очень удобным и полезным для инженеров и научных работников.
Для обозначения мнимой единицы в языке MatLAB зарезервированы два имени i и j. Ввод с клавиатуры значения комплексного числа осуществляется путем записи в командное окно строки вида:
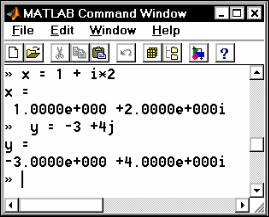
<имя комплексной переменной> = <значение ДЧ> + i [j] *<значение МЧ>,
где ДЧ - действительная часть комплексного числа, МЧ - мнимая часть. Например:
Рис. 1.10
Из приведенного примера видно, в каком виде система выводит комплексные числа на экран (и на печать).
1.2.4. Элементарные математические функции
Общая форма использования функции в MatLAB такова:
<имя результата> = <имя функции>(<перечень аргументов или их значений>).
В языке MatLAB предусмотрены следующие элементарные арифметические функции.
sin(Z) |
Тригонометрические и гиперболические функции |
- синус числа Z; |
|
sinh(Z) |
- гиперболический синус; |
asin(Z) |
- арксинус (в радианах, в диапазоне от -π /2 к +π /2); |
asinh(Z) |
- обратный гиперболический синус; |
cos(Z) |
- косинус; |
cosh(Z) |
- гиперболический косинус; |
acos(Z) |
- арккосинус (в диапазоне от 0 к π ); |
acosh(Z) |
- обратный гиперболический косинус; |
tan(Z) |
- тангенс; |
tanh(Z) |
- гиперболический тангенс; |
atan(Z) |
- арктангенс (в диапазоне от -π /2 к +π /2); |
1. 2. Операции с числами |
18 |
atan2(X,Y) - четырехквадрантный арктангенс (угол в диапазоне от -π до +π между горизонтальным правым лучом и лучом, который проходит через точку с координатами X и Y);
atanh(Z) |
- обратный гиперболический тангенс; |
|
sec(Z) |
- секанс; |
|
sech(Z) |
- гиперболический секанс; |
|
asec(Z) |
- арксеканс; |
|
asech(Z) |
- обратный гиперболический секанс; |
|
csc(Z) |
- косеканс; |
|
csch(Z) |
- гиперболический косеканс; |
|
acsc(Z) |
- арккосеканс; |
|
acsch(Z) |
- обратный гиперболический косеканс; |
|
cot(Z) |
- котангенс; |
|
coth(Z) |
- гиперболический котангенс; |
|
acot(Z) |
- арккотангенс; |
|
acoth(Z) |
- обратный гиперболический котангенс. |
|
exp(Z) |
|
Экспоненциальные функции |
- экспонента числа Z; |
||
log(Z) |
- натуральный логарифм; |
|
log10(Z) |
- десятичный логарифм; |
|
sqrt(Z) |
- |
квадратный корень из числа Z; |
abs(Z) |
- |
модуль числа Z. |
fix(Z) |
|
Целочисленные функции |
- округление к ближайшему целому в сторону нуля; |
||
floor(Z) |
- округление к ближайшему целому в сторону отрицательной бес- |
|
конечности; |
|
|
ceil(Z) |
- |
округление к ближайшему целому в сторону положительной |
бесконечности; |
|
|
round(Z) |
- обычное округление числа Z к ближайшему целому; |
|
mod(X,Y) |
- целочисленное деление X на Y; |
|
rem(X,Y) |
- вычисление остатка от деления X на Y; |
|
sign(Z) |
- вычисление сигнум-функції числа Z |
|
|
|
(0 при Z=0, -1 при Z<0, 1 при Z>0). |
1.2.5. Специальные математические функции
Кроме элементарных в языке MatLAB предусмотрен целый ряд специальных математических функций. Ниже приведен перечень и краткое содержание этих функций. Правила обращения к ним и использования пользователь может отыскать в описаниях этих функций, которые выводятся на экран, если набрать команду help и указать в той же строке имя функции.
Функции преобразования координат
1. 2. Операции с числами |
19 |
cart2sph |
- преобразование декартовых координат в сферические; |
cart2pol |
- преобразование декартовых координат в полярные; |
pol2cart |
- преобразование полярных координат в декартовые; |
sph2cart |
- преобразование сферических координат в декартовые. |
besselj |
Функции Бесселя |
- функция Бесселя первого рода; |
|
bessely |
- функция Бесселя второго рода; |
besseli |
- модифицированная функция Бесселя первого рода; |
besselk |
- модифицированная функция Бесселя второго рода. |
beta |
Бета-функции |
- бета-функция; |
|
betainc |
- неполная бета-функция; |
betaln |
- логарифм бета-функции. |
gamma |
Гамма-функции |
- гамма-функция; |
|
gammainc - неполная гамма-функция; |
|
gammaln |
- логарифм гамма-функции. |
ellipj |
Эллиптические функции и интегралы |
- эллиптические функции Якобе; |
|
ellipke |
- полный эллиптический интеграл; |
expint |
- функция экспоненциального интеграла. |
erf |
Функции ошибок |
- функция ошибок; |
|
erfc |
- дополнительная функция ошибок; |
erfcx |
- масштабированная дополнительная функция ошибок; |
erfinv |
- обратная функция ошибок. |
gcd |
Другие функции |
- наибольший общий делитель; |
|
lcm |
- наименьшее общее кратное; |
legendre |
- обобщенная функция Лежандра; |
log2 |
- логарифм по основанию 2; |
pow2 |
- возведение 2 в указанную степень; |
rat |
- представление числа в виде рациональной дроби; |
rats |
- представление чисел в виде рациональной дроби. |