
- •Начала программирования в среде MatLab
- •Содержание
- •Предисловие
- •Введение
- •1. MatLAB как научный калькулятор
- •1.1. Командное окно
- •1.2. Операции с числами
- •1.2.1. Ввод действительных чисел
- •1.2.2. Простейшие арифметические действия
- •1.2.3. Ввод комплексных чисел
- •1.2.4. Элементарные математические функции
- •1.2.5. Специальные математические функции
- •1.2.6. Элементарные действия с комплексными числами
- •1.2.7. Функции комплексного аргумента
- •1.2.8. Задания
- •1.2.9. Вопросы
- •1.3. Простейшие операции с векторами и матрицами
- •1.3.1. Ввод векторов и матриц
- •1.3.2. Формирование векторов и матриц
- •1.3.3. Извлечение и вставка частей матриц
- •1.3.4. Действия над векторами
- •1.3.5. Поэлементное преобразование матриц
- •1.3.6. Матричные действия над матрицами
- •1.3.7. Матричные функции
- •1.3.8. Задания
- •1.3.9. Вопросы
- •1.4. Функции прикладной численной математики
- •1.4.1. Операции с полиномами
- •1.4.2. Обработка данных измерений
- •1.4.3. Функции линейной алгебры
- •1.4.4. Аппроксимация и интерполяция данных
- •1.4.5. Векторная фильтрация и спектральный анализ
- •1.4.6. Задания
- •1.4.7. Вопросы
- •1.5. Построение простейших графиков
- •1.5.1. Процедура plot
- •1.5.2. Специальные графики
- •1.5.3. Дополнительные функции графического окна
- •1.5.5. Задания
- •1.5.6. Вопросы
- •1.6. Операторы управления вычислительным процессом
- •1.6.1. Оператор условного перехода
- •1.6.2. Оператор переключения
- •1.6.3. Операторы цикла
- •1.6.4. Задания
- •1.6.5. Вопросы
- •2. Программирование в среде MatLAB
- •2.1. Функции функций
- •2.2. Создание М-файлов
- •2.2.1. Особенности создания М-файлов
- •2.3.1. Общие требования к построению
- •2.3.2. Типовое оформление процедуры-функции
- •2.3.3. Задания
- •2.3.4. Вопросы
- •2.4. Создание Script-файлов
- •2.4.1. Основные особенности Script-файлов
- •2.4.2. Ввод и вывод информации в диалоговом режиме
- •2.4.3. Организация повторения действий
- •2.4.4. Организация изменения данных в диалоговом режиме
- •2.4.5. Типовая структура и оформление Script-файла
- •2.5. Графическое оформление результатов
- •2.5.1. Общие требования к представлению графической информации
- •2.5.2. Разбивка графического окна на подокна
- •2.5.3. Вывод текста в графическое окно (подокно)
- •2.6. Создание функций от функций
- •2.6.1. Процедура feval
- •2.6.2. Примеры создания процедур от функций
- •2.6.3. Задания
- •2.7. Пример создания сложной программы
- •2.7.1. Программа моделирования движения маятника
- •2.7.2. Задания
- •3.1. Функции меню командного окна
- •3.1.2. Другие меню командного окна
- •3.1.3. Панель инструментов
- •3.2. Команды общего назначения
- •3.3. Создание М-книги
- •3.3.1. Начало новой М-книги
- •3.3.2. Написание М-книги
- •3.3.3. Редактирование М-книги
- •3.3.4. Преобразование документа WORD в М-книгу
- •3.3.6. Изменение параметров вывода результатов
- •4. Классы вычислительных объектов
- •4.1. Основные классы объектов
- •4.1.1. Класс символьных строк (char)
- •4.1.2. Класс записей (struct)
- •4.1.3. Класс ячеек (cell)
- •4.2. Производные классы MatLAB
- •4.2.1. Класс объектов Inline
- •4.2.2. Классы пакета CONTROL
- •4.3. Пример создания нового класса polynom
- •4.3.1. Создание подкаталога @polynom
- •4.3.2. Создание конструктора
- •4.3.3. Создание процедуры символьного представления polynom-объекта.
- •4.4. Создание методов нового класса
- •5.1. Формирование типовых процессов
- •5.1.1. Формирование одиночных импульных процессов
- •5.1.2. Формирование колебаний
- •5.2.1. Основы линейной фильтрации
- •5.2.2. Формирование случайных процессов
- •5.3. Процедуры спектрального (частотного) и статистического анализа процессов
- •5.3.1. Основы спектрального и статистического анализа
- •5.3.2. Примеры спектрального анализа
- •5.3.3. Статистический анализ
- •5.4. Проектирование фильтров
- •5.4.1. Формы представления фильтров и их преобразования
- •5.4.2. Разработка аналоговых фильтров
- •5.4.3. Проектирование БИХ-фильтров
- •5.5. Графические и интерактивные средства
- •5.5.1. Графические средства пакета SIGNAL
- •5.5.2. Интерактивная оболочка SPTOOL
- •6.1. Ввод и преобразование моделей
- •6.2. Получение информации о модели
- •6.3. Анализ системы
- •6.4. Интерактивный "обозреватель" ltiview
- •6.5. Синтез системы
- •7.1. Общая характеристика пакета SimuLink
- •7.1.1. Запуск SimuLink
- •7.1.2. Библиотека модулей (блоков)
- •7.1.3. Раздел Sinks (приемники)
- •7.1.4. Раздел Sources (Источники)
- •7.1.5. Раздел Сontinuous
- •7.1.6. Раздел Discrete
- •7.1.7. Раздел Math
- •7.1.8. Раздел Functions & Tables
- •7.1.9. Раздел Nonlinear
- •7.1.10. Раздел Signals & Systems
- •7.2. Построение блок-схем
- •7.2.1. Выделение объектов
- •7.2.2. Оперирование с блоками
- •7.2.3. Проведение соединительных линий
- •7.2.4. Проставление меток сигналов и комментариев
- •7.2.5. Создание подсистем
- •7.2.6. Запись и распечатка блок-схемы S-модели
- •7.3. Примеры моделирования
- •7.3.1. Моделирование поведения физического маятника
- •7.3.2. Моделирование поведения гироскопа в кардановом подвесе
- •7.4. Объединение S-моделей с программами MatLAB
- •7.4.2. Функции пересечения нуля
- •7.4.5. Образование S-блоков путем использования программ MatLab. S-функции
- •7.4.6. Пример создания S-функции
- •7.5.1. Создание библиотеки
- •7.5.2. Маскировка блоков
- •7.5.3. Моделирование процесса ориентации космического аппарата
- •Послесловие
- •Предметный указатель
- •Указатель операторов, команд, функций и функциональных блоков MatLAB
6.4. Интерактивный "обозреватель" ltiview |
295 |
|
|
|
|
6.4. Интерактивный "обозреватель" ltiview
Набирая в командном окне MatLAB команду ltiview, можно вызывать окно так называемого "обозревателя" LTI-объектов, что позволяет в интерактивном режиме "строить" в этом окне практически все вышеуказанные графики, причем для нескольких систем синхронно:
ltiview
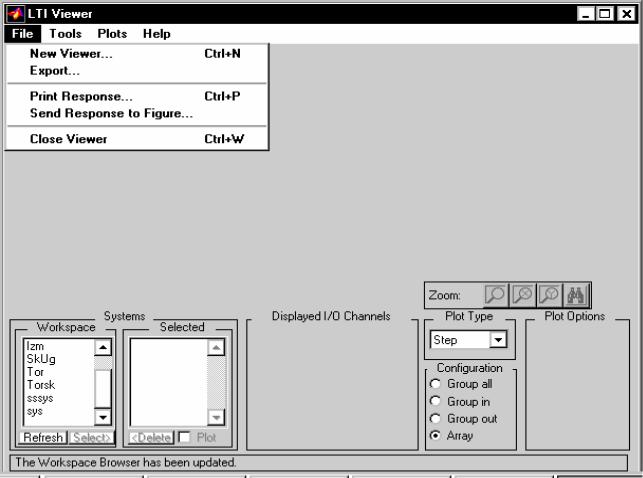
При этом на экране появляется новое окно LTIViewer (рис. 6.12 ).
Рис. 6.12
Это окно состоит из нескольких частей. Главное место в нем занимает графическое поле, в котором строятся разнообразные графики. При первом обращении к обозревателю оно пусто. В левой нижней части расположены два окошка Workspace и Selected. В первом из них отображены те LTI-объекты, которые находятся в это время в рабочем пространстве системы MatLAB (на рис. 6.12 - это система sys бокового движения торпеды, созданная ранее). В втором отображаются LTI-объекты, которые загружены в среду обозревателя. В начале работы с обозревателем оно также является пустым.
По правой стороне внизу расположено окошко с выпадающим меню, которое содержит перечень графических процедур, которые можно выполнить. Еще правее расположены окошки, оперирование которыми позволяет определить не-

6.4. Интерактивный "обозреватель" ltiview |
296 |
|
|
|
|
которые числовые характеристики соответствующего графика. Для этого надлежит в соответствующем окошке поставить "галочку" с помощью мыши.
Работу с обозревателем необходимо начинать с "загрузки" в его среду тех LTI-объектов, которые нужно анализировать. Это делается таким образом.
С помощью мыши следует выделить в окошке Workspace имена LTIобъектов, которые нужно исследовать. Потом "нажать мышкой" на надпись '<Select>' под окошком справа. Соответствующее имя должно появиться в окошке Selected рядом (см. рис. 6.13). Причем по левую сторону имя сопровождается знаком '+', а по правую сторону от него указан в скобках цвет линии графика, которая отвечает LTI-объекту с этим именем. Синхронно в графическом поле появляется график реакции избранной системы на входное действие в виде единичной ступеньки (рис. 6.13 ), так как в обычном состоянии в окошке справа установлено
Step.
Рис. 6.13
Если в этом окошке "нажать" кнопку выпадающего меню, то оно предоставит такие альтернативные возможности обозревателя:
Step
Impulse
Bode
6.4. Интерактивный "обозреватель" ltiview |
297 |
|
|
|
|
Nyquist
Nichols
Sigma
PoleZero
Lsim
Initial
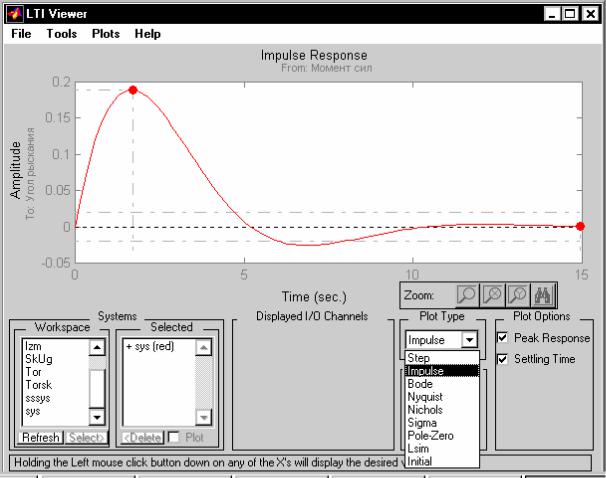
Как видим, эти альтернативы полностью совпадают с ранее рассмотренными одноименными процедурами и потому следует ожидать, что их избрание приведет к построению тех же графиков. Например, выбирая раздел Impulse, получим картину, изображенную на рис. 6.14.
Внижнем крайне правом углу окна расположены окошки, которые позволяют отметить те параметры соответствующего графика, которые можно отсчитать по графику.
Вкачестве примера на рис. 6.13 и 6.14 отмечены ("галочками" в соответствующих окошках) все возможные параметры. Поэтому на графиках появились точки, которые отвечают искомым параметрам.
Рис. 6.14
6.4. Интерактивный "обозреватель" ltiview |
298 |
|
|
|
|
Вид графиков можно изменять, используя меню окна обозревателя. К примеру, раздел File меню окна обозревателя (см. рис. 6.12 ) вызывает дополнительное меню с такими разделами:
New Viewer - открыть новый обозреватель; при избрании этого раздела "мышкой" на экране образовывается еще одно, дополнительное окно такого же обозревателя, в котором можно построить иные нужные графики;
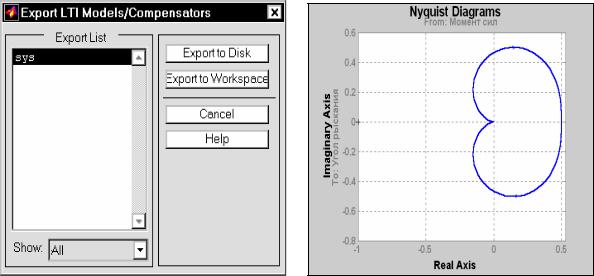
Export - экспортировать LTI-объект; избрание этого раздела приводит к появлению на экране окна Export LTI Models/Compensators (рис. 6.15), ко-
торое позволяет записать использованные LTI-объекты (имена которых находятся в окошке по левую сторону) или в МАТ-файл (окошко Export to Disk), или в рабочее пространство (Export to Workspace);
Print Response - распечатать графики на принтере;
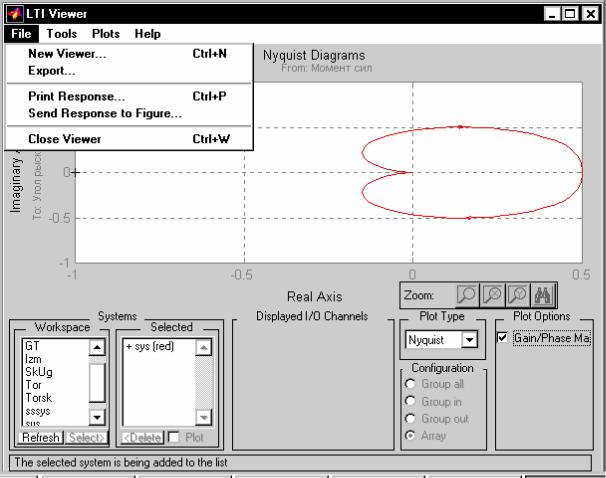
Send Response to Figure - расположить график в отдельном графическом окне (фигуре); эта команда приводит к появлению на экране дополнительного окна LTI Viewer Responses, в котором в объеме всего окна располагается тот же график, который находится к тому времени в графическом поле окна LTI Viewer; это удобно с двух точек зрения: во-первых, график в этом окне имеет более обозримую и удобную форму для его распечатывания на принтере, а во-вторых, что более важно, новое окно дает возможность образовать "копию фигуры"; последняя создается так: используется раздел Edit в меню нового окна, потом в появившемся подменю выбирается раздел Copy Figure - и содержимое окна запоминается в буфере памяти ПК; если теперь перейти в окно какого-нибудь редактора (графического или текстового) и нажать клавиши <Shift> + <Insert>, то в окне этого редактора появится запомненное изображение; именно таким образом получен рис. 6.16, содержащий годограф Найквиста для исследуемой системы (см. рис. 6.17 );
Рис. 6.15 Рис. 6.16
Close Viewer - "закрыть" окно обозревателя.
|
6.4. Интерактивный "обозреватель" ltiview |
299 |
|
|
|
|
|
|
|
|
|
Рис. 6.17
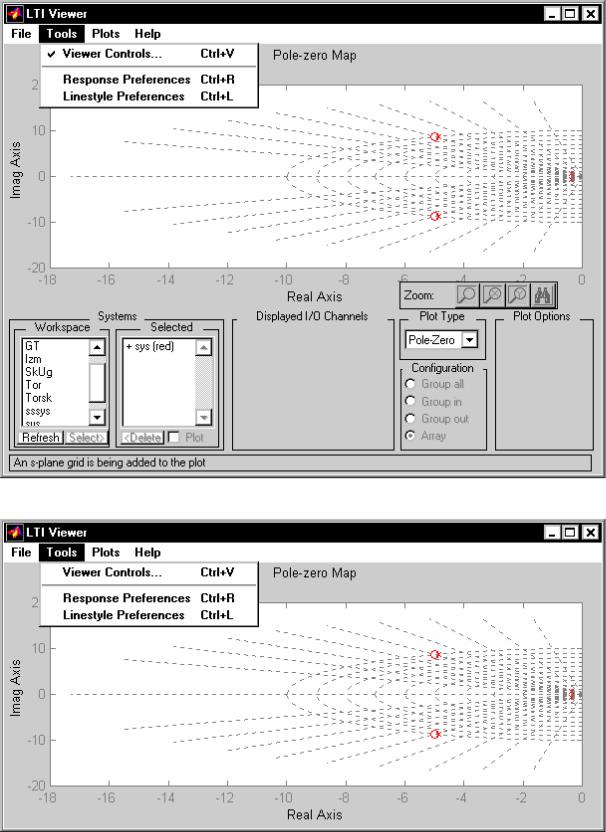
Перейдем к следующему разделу меню окна LTI Viewer под названием Tools. "Нажав" на него, получим подменю (рис. 6.18), состоящее из трех таких разделов:
Viewer Controls (Управление Обозревателем), которое добавляет или уничтожает нижнюю половину окна LTI Viewer, в которой располагаются окошки управления выводом графической информации в верхнюю половину окна; каждое нажатие на этот раздел приводит к исчезновению "галочки" рядом с названием раздела (если она перед этим была) или к появлению ее (если ее не было); по умолчанию "галочка" есть, и потому вся управляющая половина изображена в окне LTI Viewer; если теперь "нажать мышкой" на Viewer Controls, получим в окне картину, представленную на рис. 6.19 ;
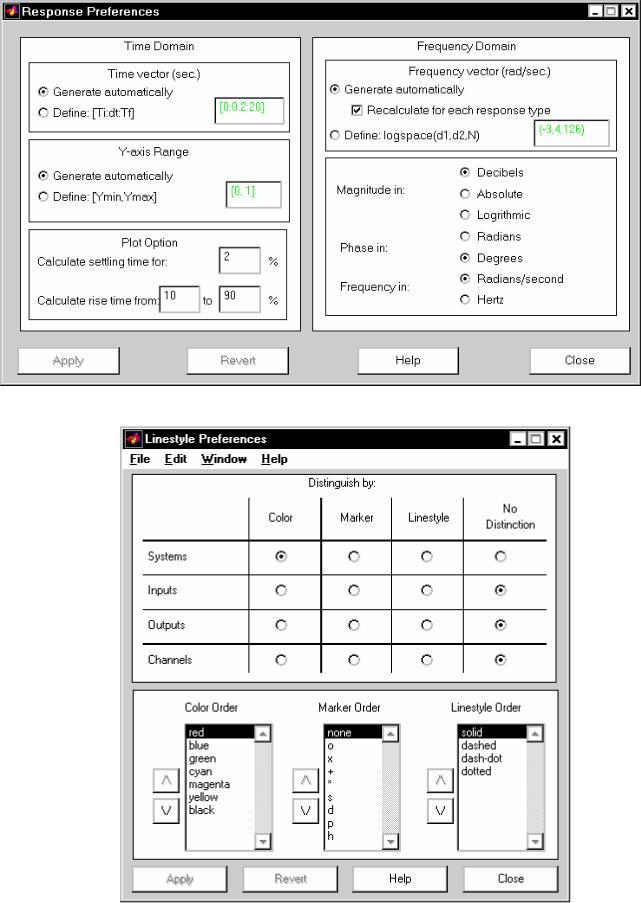
Response Preferences (Свойства Графиков); нажатие на него приводит к появлению нового окна с таким же названием (рис. 6.20); благодаря этому окну можно установить собственные желательные диапазоны изменений координат, изменить единицы измерения амплитуды и частоты, установить собственные определения времени установления и времени возрастания переходного процесса и т. п.;
6.4. Интерактивный "обозреватель" ltiview |
300 |
|
|
|
|
Рис. 6.18
Рис. 6.19
6.4. Интерактивный "обозреватель" ltiview |
301 |
|
|
|
|
Рис. 6.20
Рис. 6.21
6.4. Интерактивный "обозреватель" ltiview |
302 |
|
|
|
|
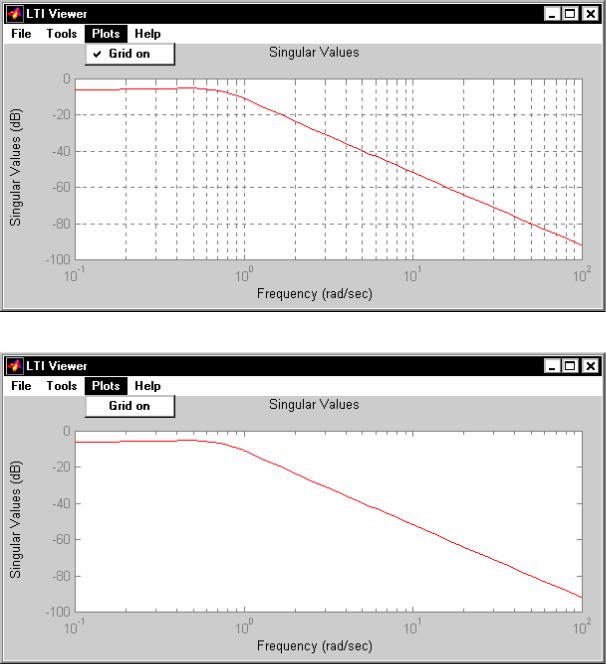
Linestyle Preferences (Свойства и стили линий), которое позволяет по собственному усмотрению устанавливать цвета, толщину и стили линий графического изображения; для этого достаточно "нажать мышкой" на этот раздел, и в появившемся окне (рис. 6.21 ) установить желательные параметры.
В следующем разделе меню обозревателя Plots (Графики) есть только один раздел дополнительного меню - Grid On (Сетка Установлена) - рядом с которым есть или нет "галочка" (рис. 6.22). Если "галочка" есть, графики сопровождаются сеткой из координатных линий, например так, как изображено на рис. 6.22.
Рис. 6.22
Рис. 6.23
