Если в четырехугольник можно вписать окружность, то суммы противоположных сторон
четырехугольника равны Радиус окружности, проведенный в
точку касания перпендикулярен касательной
Радиус окружности равен половине диаметра
33 |
В |
|
|
АВСD – ромб. |
||
|
|
|
|||
А |
|
|
Найти r. |
Повторение |
|
r |
С |
|
|
(4) |
|
H 30 |
90 |
|
Проведем СH AD, |
||
|
получим |
|
|
||
D |
|
|
прямоугольный ∆CDH |
||
|
|
CH 1 CD 1 90 |
45 |
||
|
|
|
2 |
2 |
|
r 12 d 12 CD 12 45 22,5
Ответ: 22,5.
34
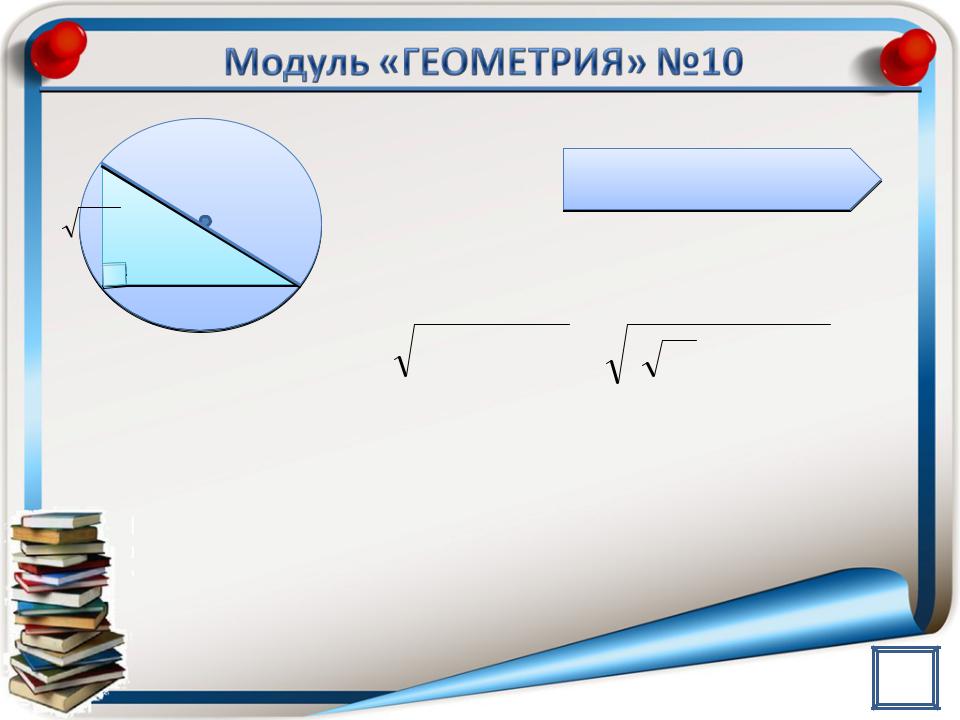
Радиус окружности, проведенный в точку касания перпендикулярен касательной
Перпендикуляры между параллельными прямыми равны
Впрямоугольном треугольнике катет, лежащий против угла в 30 равен половине гипотенузы
Радиус окружности равен половине диаметра
35 |
В |
|
|
|
Найти r. |
Повторение |
|
|
|
|
|
|||
135 |
|
r |
|
|
(3) |
|
|
|
|
|
|
||
С |
11 |
А |
По теореме Пифагора в ∆BCH |
|
||
|
|
|
АB BC АC2 |
( 135)2 112 |
16 |
|
r 12 d 12 AB 12 16 8
Ответ: 8.
36
Прямой угол, вписанный в окружность опирается на диаметр окружности
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Радиус окружности равен половине диаметра
37 |
В |
|
С |
АВСD – трапеция, P |
=12. |
|
|
|
|
∆ABCD |
|
|
M |
|
К |
Найти боковую сторону |
|
|
5 |
трапеции. |
Повторение |
|||
А |
|
D |
|
(3) |
|
|
|
|
|
||
|
|
|
MK AD BC |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
|
AD+BC=2MK=2∙5 |
|
|
|
||
AB |
1 |
=10 |
(AD BC)) |
1 |
(12 10) 1 |
||
2 |
(P |
2 |
|||||
|
ABCD |
|
|
|
|||
Ответ: 6.
38
Средняя линия трапеции равна полусумме оснований трапеции
Описать окружность можно только около равнобедренной трапеции
Периметр многоугольника – это сумма длин всех сторон многоугольника
39 |