
Sizov_Behovyh_Molecular_Physics
.pdf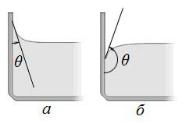
(1)
Коэффициент σ называется коэффициентом поверхностного на-
тяжения (σ > 0). Таким образом, коэффициент поверхностного на-
тяжения равен работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.
Единица измерения коэффициента поверхностного натяжения жидкости в СИ: 1 Дж/м2 (джоуль на метр квадратный).
Следовательно, молекулы поверхностного слоя жидкости обладают избыточной по сравнению с молекулами внутри жидкости потенциальной энергией. Из механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии. Отсюда следует, что свободная поверхность жидкости стремится сократить свою площадь. По этой причине свободная капля жидкости принимает шарообразную форму. Жидкость ведет себя так, как будто по касательной к ее поверхности действуют силы, сокращающие (стягивающие) эту поверхность. Эти силы называются сила-
ми поверхностного натяжения.
Сила поверхностного натяжения пропорциональна числу молекул, прилегающих к контуру на поверхности жидкости, которое, в свою очередь, пропорционально длине контура:
F =σ L. |
(2) |
Таким образом, коэффициент поверхностного натяжения (σ)
может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.
В этом случае единицей измерения коэффициента поверхностного натяжения в СИ является 1 Н/м (ньютон на метр). Легко показать равенство единиц измерения 1 Н/м = 1 Дж/м2.
Вблизи границы между жидкостью, твердым телом и газом форма свободной поверхности жидкости зависит от сил взаимодействия молекул жидкости с молекулами твердого тела (взаимодействием с молекулами газа (или пара) можно пренебречь). Если эти силы больше сил взаимодействия между молекулами самой жидкости, то жидкость смачивает поверхность твердого тела. В этом случае
жидкость подходит к поверхности твердого тела под некоторым острым углом θ (рис. 2, а), характерным для данной пары жидкость – твердое тело. Угол θ называется краевым углом. Если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого
88
7.Как рассчитываются погрешности при прямых измерениях?
8.Как рассчитываются погрешности при косвенных измерениях?
Лабораторная работа № 2
ИЗУЧЕНИЕ УПРУГОГО ЦЕНТРАЛЬНОГО УДАРА ШАРОВ
Цель работы: проверить закон сохранения импульса на примере упругого соударения двух шаров, подвешенных на нитях; определить среднюю силу удара.
Оборудование: прибор для исследования столкновения шаров.
Основные теоретические сведения
Под ударом (или соударением) понимают столкновение двух или более тел, при котором взаимодействие длится очень короткое время. Удар сопровождается деформациями (изменением формы и размеров) взаимодействующих тел, в результате которых возникают столь значительные внутренние силы, что роль всех постоянно действующих внешних сил можно считать ничтожной. Поэтому соударяющиеся тела можно рассматривать как замкнутую систему и применять к ней законы сохранения.
Удар называется центральным, если скорости тел до удара направлены вдоль прямой линии, проходящей через их центры масс. Для простоты будем рассматривать только центральные абсолютно упругие и абсолютно неупругие удары.
Абсолютно упругий удар – столкновение двух тел, в результате которого в обоих взаимодействующих телах не остается никаких деформаций, и вся кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию. Идеально упругих ударов в природе не существуют, так как всегда часть энергии идет на необратимую деформацию тел и увеличение их внутренней энергии. Однако для некоторых тел, например, для стальных шариков, потерями механической энергии можно пренебречь.
К абсолютно упругому удару применимы закон сохранения количества движения (импульса) и закон сохранения энергии, так как в этом случае действуют только консервативные силы, работа которых не зависит от формы траектории движения.
21

r |
|
|
|
|
|
||
Векторная физическая величина, равная произведению массы |
|||||||
тела на его скорость, т.е. pi = mi υi |
|
называется импульсом тела. Еди- |
|||||
ница измерения импульса тела в |
СИ: [P]=1кг 1 |
м |
=1 |
кг м |
(кило- |
||
с |
с |
||||||
|
|
|
|
|
|||
грамм-метр на секунду).
Закон сохранения импульса: векторная сумма импульсов тел, составляющих замкнутую систему, остается неизменной с течением времени. Математическое выражение этого закона имеет вид:
∑n rpi = const .
i=1
Полная механическая энергия складывается из кинетической и потенциальной.
Кинетическая энергия ( Eк ) – это энергия механического движения. Для поступательного движения она определяется по формуле:
Ек = m2υ2 = 2p2m ,
где m – масса тела; υ – скорость движения тела; p – импульс тела.
Причем выражение для кинетической энергии, записанное через импульс, остается неизменным при переходе от классической механики (ньютоновской) к квантовой (механике микромира).
Потенциальная энергия (Ep ) – это механическая энергия, опре-
деляемая взаимным расположением взаимодействующих тел и характером сил между ними. В поле силы тяжести ее определяют из выражения:
Еp = m g h,
где h– расстояние, отчитываемое от нулевого уровня до центра масс тела, для которого Ep = 0.
Так как начало отсчета выбирается произвольно, то потенциальная энергия может принимать отрицательные значения (кинетическая энергия всегда положительна).
Как и для любых других видов энергии единицей измерения для вышеназванных в СИ является 1Дж (джоуль).
Закон сохранения энергии: полная механическая энергия тел, движущихся в поле консервативных сил, остается неизменной с течением времени. Математически это можно записать в виде:
E = const
22
Лабораторная работа №13
ИЗМЕРЕНИЕ КОЭФФИЦИЕНТА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ МЕТОДОМ ОТРЫВА КОЛЬЦА
Цель работы: изучить явление поверхностного натяжения жидкости.
Оборудование: экспериментальная установка, исследуемая жидкость, штангенциркуль.
Основные теоретические сведения
|
Наиболее |
интересной |
|
|
особенностью |
жидкостей |
|
|
является наличие свободной |
||
|
поверхности. Жидкость, в |
||
|
отличие от газов, не запол- |
||
|
няет весь объем сосуда, в |
||
|
который она налита. Между |
||
Рис. 1. Взаимодействие молекул |
жидкостью и газом (или па- |
||
ром) образуется граница |
|||
жидкости |
|||
раздела, которая |
находится |
||
|
|||
вособых условиях по сравнению с остальной массой жидкости. Молекулы в пограничном слое жидкости (рис. 1, в, г), в отличие от молекул
вее глубине (рис. 1, а, б), окружены другими молекулами той же жидкости не со всех сторон. Силы межмолекулярного взаимодействия, действующие на одну из молекул внутри жидкости со стороны соседних молекул, в среднем взаимно скомпенсированы. Любая молекула в пограничном слое притягивается молекулами, находящимися внутри жидкости (силами, действующими на данную молекулу жидкости со стороны молекул газа (или пара) можно пренебречь). В результате по-
является некоторая равнодействующая сила F1 (или F2 ), направлен-
ная внутрь жидкости. Если молекула переместится с поверхности внутрь жидкости, силы межмолекулярного взаимодействия совершат положительную работу. Наоборот, чтобы переместить некоторое количество молекул из глубины жидкости на поверхность (т.е. увеличить площадь поверхности жидкости), внешние силы должны совершить работу ∆Aвнеш, пропорциональную изменению ∆S площади поверхности:
87

Обработка результатов измерений
1.Для каждого опыта вычислите значение γ, пользуясь форму-
лой (18).
2.Рассчитайте значения i, cp и cV, пользуясь формулами (19), (20), (21). Запишите результаты вычислений в таблицу.
3.Вычислите, используя формулу (3), для каждого опыта значения Cрµ и CVµ. Запишите результаты вычислений в таблицу.
4.Найдите средние арифметические значения измеренных величин и сопоставьте их с теоретическими.
Теоретические значения рассчитать, приняв воздух за двухатомныйгаз (i = 5).
5.Найдите отклонение измеренных значений γ, cp, cV ,Cрµ, CVµ от их теоретических значений как отношение разности измеренных и теоретических значений, взятых по модулю к теоретическим значени-
ям, например, для γ:
E = γтеор −γпракт 100%.
γтеор
6.Проверьте, используя средние значения молярных теплоёмкостей при постоянном давлении и постоянном объёме справедливость уравнения Майера и сделайте вывод, объяснив несовпадение результатов с теоретическими.
Контрольные вопросы
1.Что такое теплоемкость газа?
2.Дайте определение понятия «число степеней свободы моле-
кулы».
3.Как связаны cp и cV с числом степеней свободы молекул газа
i?
4.Как связаны между собой Сp и СV?
5.Какой процесс называется адиабатическим? Почему при адиабатическом процессе изменяется температура системы?
6.Сформулируйте первое начало термодинамики.
7.Выведите уравнение Пуассона.
8.Какие изопроцессы используются при выполнении данной
работы?
9.Объясните, почему измеренные значения не совпадают с теоретическими значениями этих величин?
86
или
Ek1 + Ep1 = Ek2 + Ep2 ,
где Ek1 и Ek2 – кинетические энергии системы в двух состояниях;
Ep1 и Ep2 – потенциальные энергии системы в тех же двух состоя-
ниях.
Абсолютно неупругий удар – столкновение двух тел, в результате которого тела объединяются, двигаясь дальше как единое целое. При таком соударении вследствие пластической деформации часть кинетической энергии шаров идет на увеличение их внутренней энергии. Поэтому закон сохранения механической энергии в этом случае не соблюдается. Абсолютно неупругий удар – пример того, как происходит «потеря» механической энергии под действием диссипативных сил, работа которых зависит от формы траектории.
Обоснование метода
Рис. 1. Начальное состояние системы
Эксперимент заключается в определении импульсов (количества движения) шаров до и после столкновения и в сравнении полученных результатов.
Для упрощения задачи будем рассматривать упругий центральный удар шаров одинаковой массы m1 = m2 = m (рис. 1).
Количество движения шаров до столкновения (при покоящемся ударяемом шаре 2) определяется по формуле:
p = m1 υ1 , |
(1) |
где |
m – масса 1 шара (ударяющего) вместе с подвеской; |
|
r |
1 |
|
υ1 |
– скорость 1 шара перед ударом. |
|
|
В проекциях на ось х это выражение имеет вид: |
|
|
p = m1 υ1 . |
(2) |
Величину скорости υ1 можно определить, используя закон со-
23
хранения механической энергии. Кинетическая энергия, которую имеет шар 1 к началу столкновения, равна потенциальной энергии поднятого шара в момент начала его движения:
m g h = |
m υ |
2 |
, |
(3) |
1 1 |
|
|||
|
|
|||
1 |
2 |
|
|
|
|
|
|
|
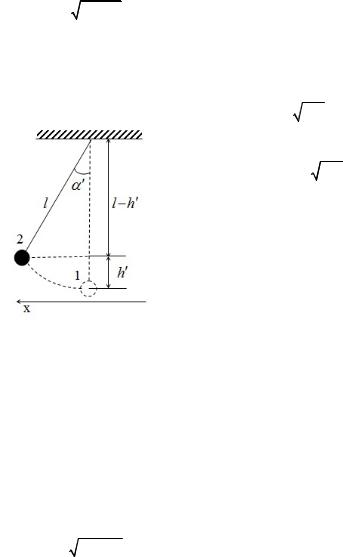
отсюда υ1 = 2 g h . Высоту подъема шара h выразим через угол α ,
с которого шар был пущен и длину подвеса l . Из рисунка 1 следует: l −h =l cosα , откуда:
h =l (1−cos(α)) = 2 l sin2(α /2). |
(4) |
Окончательное выражение для начальной скорости имеет вид:
|
|
υ1 = 2 g l sin(α /2) , |
(5) |
|
|
а для импульса системы до соударе- |
|||
|
ния: |
|
|
|
|
|
p = 2 m1 |
g l sin(α /2). |
(6) |
|
|
При упругом |
соударении двух |
|
|
шаров одинаковой массы они обмени- |
|||
|
ваются скоростями, поэтому если до |
|||
|
взаимодействия шар 2 покоился, то |
|||
|
после соударения он приобретет ско- |
|||
|
рость шара 1, а сам шар 1 остановится. |
|||
|
В этом случае суммарный импульс |
|||
|
системы после соударения определя- |
|||
Рис. 2. Конечное состояние |
ется выражением: |
|
|
|
|
p′= m2 υ2′ , |
(7) |
||
системы |
|
|||
r |
где |
m2 – масса шара 2 (ударяемого) |
||
вместе с подвеской; |
|
|
|
|
υ2′ – его скорость после удара. |
|
|
|
|
В проекциях на ось х это выражение имеет вид: |
|
|||
|
p′ = m2 υ2′. |
|
(8) |
|
Величину скорости после удара υ2′ определим, используя закон сохранения энергии:
m2 υ2′2 |
= m2 g h′, |
(9) |
|
2 |
|||
|
|
откуда υ2′ = 2 g h′ .
Из рисунка 2 следует:
24
i = |
2 |
; |
|
|
(19) |
|||
|
|
γ − 1 |
|
|
||||
|
|
|
R |
|
|
|
||
c = |
|
|
|
; |
(20) |
|||
µ(γ −1) |
||||||||
V |
|
|
|
|||||
cp = |
|
|
γR |
|
|
|
(21) |
|
|
µ(γ −1). |
|||||||
|
|
|||||||
Порядок выполнения работы
1. Подготовьте таблицу для записи результатов измерений и вычислений:
№ |
h1, |
|
h2, |
|
cp, |
|
|
cV, |
|
|
Сpµ, |
|
|
СVµ, |
|
|
i |
мм вод. |
|
мм вод. |
|
Дж |
|
|
Дж |
|
|
Дж |
|
|
Дж |
|
γ |
||
п/п |
ст. |
|
ст. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
кг К |
|
|
кг К |
|
|
моль К |
|
|
моль К |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Среднее |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Установите кран К в открытое положение.
3.Медленно нагнетайте насосом воздух в баллон до разницы уровней в коленах манометра 150-200 мм вод. ст., после чего закройте кран ( см. рис.).
Внимание! Будьте осторожны! При большой разнице давлений
вколенах манометра вода может фонтаном вылиться наружу!
4.Когда уровень воды в коленах манометра перестанет изме-
няться, произведите отсчет величины h1 и занесите результат в таблицу.
5.Выньте кран К и, дождавшись равенства уровней жидкости в коленах манометра, быстро закройте его.
6.После того как уровень воды в коленах манометра перестанет
изменяться, произведите отсчет величины h2 и занесите результат в таблицу.
7.Повторите опыт 5 раз по пунктам 2 - 6 при нескольких различных значениях избыточного давления.
85

В течение всех рассмотренных процессов масса газа в баллоне больше или равна начальной массе газа m0, которую назовем рабочей массой. Накачиваемый и выпускаемый газ служат лишь для сжатия и расширения рабочей массы газа.
Уравнение адиабаты (11) для рассматриваемых процессов запишется в виде
Температура T1 |
p11 − γ |
T 0γ |
= |
p 01 − γ T1 |
γ |
. |
(13) |
||||||||
после изохорического нагревания становится |
|||||||||||||||
равной T0, значит, можно записать: |
|
|
|
|
|
|
|
|
|
|
|||||
Отсюда |
|
|
|
p0/T1 = p2/T0. |
|
|
|
|
|
(14) |
|||||
|
|
|
T1 = p0T0/p2. |
|
|
|
|
|
(15) |
||||||
|
|
|
|
|
|
|
|
|
|||||||
Подставляя выражение (15) в (14) и проведя очевидное сокра- |
|||||||||||||||
щение, получим |
|
|
|
|
|
|
p0 |
|
|
|
|
|
|
|
|
|
|
|
|
1−γ |
|
|
|
|
|
|
|
(16) |
|||
|
|
|
|
p1 |
|
= p2γ . |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Прологарифмировав это выражение и подставив значения p1 и |
|||||||||||||||
p2, находим |
|
|
|
ln(p0 + h1) −lnp0 |
|
|
|
|
|
||||||
|
γ = |
|
|
|
= |
|
|
||||||||
|
|
|
ln(p + h ) |
−ln(p |
+ h ) |
|
|
(17) |
|||||||
|
|
|
|
0 |
1 |
0 |
2 |
|
|
|
|||||
|
|
|
ln(p0 + h1 / p0) |
|
|
|
|
|
|||||||
|
= |
|
|
= |
|
|
|
||||||||
|
ln(p |
+ h ) |
−ln(p + h ) |
|
|
|
|||||||||
|
|
|
0 |
1 |
|
0 |
|
2 |
|
|
|
|
|
|
|
|
= |
|
|
ln(1 |
+ h1 / p0) |
|
|
|
|
|
|||||
|
ln(1 + h / p ) −ln(1 |
+ h / p |
) |
|
|||||||||||
|
|
|
|
1 |
0 |
|
|
|
2 |
|
2 |
|
|
||
Так как h1 << p0 |
и h2 << p0 h1/p0 << 1и h2/p0<< 1, то для уп- |
||||||||||||||
рощения формулы (17) используем свойство логарифма ln(1 + x) ≈ x,
при x <<1. После сокращений формула (17) |
приобретает вид |
||||
γ = |
|
h1 |
|
. |
(18) |
h |
− h |
2 |
|||
1 |
|
|
|
||
Выражение (18) показывает, что определение значения γ сводится к измерению избыточных давлений h1 и h2.
Зная молярную массу воздуха (µ = 29 10-3 кг/моль) и используя измеренное значение γ, вычисляются значения числа степеней свободы i и удельные теплоемкости при постоянном объеме и при постоянном давлении (cV и сp):
84
h′ =l (1−cos(α′)) = 2 l sin2 (α′/2) . |
(10) |
Поэтому выражение для скорости υ2′ имеет вид: |
|
υ2′ = 2 g l sin(α′/2). |
(11) |
Окончательно импульс системы после удара определим из выражения:
p′ = 2 m2 g l sin(α′/2). |
(12) |
Сравнение начального суммарного импульса системы с импульсом после соударения позволяет сделать вывод о справедливости применения закона сохранения импульса к упругому удару.
Считая, что в течение времени соударения на шар действует не-
которая постоянная средняя сила F , в соответствии со вторым законом Ньютона запишем:
F = |
dp |
= m |
dυ |
|
(13) |
|||||
dt |
dt |
|||||||||
|
|
|
|
|
|
|||||
или в проекциях на ось х: |
|
dυ |
|
|
|
|
||||
|
F = m |
. |
(14) |
|||||||
|
||||||||||
|
|
|
|
|
dt |
|
||||
Формулу (14) можно переписать в виде: |
|
|||||||||
|
m dυ = F dt . |
(15) |
||||||||
Из выражения (15) следует: |
|
|
|
|
|
|
||||
|
υ1′ |
|
τ |
|
||||||
m ∫dυ = F ∫dt , |
|
|||||||||
|
υ1 |
0 |
|
|
|
|
||||
где при υ1′ = 0 : |
|
|
|
|
|
|
||||
|
m υ1 = F τ . |
(16) |
||||||||
Таким образом, с учетом (5) искомое выражение для средней |
||||||||||
силы соударения имеет вид: |
|
|
|
|
|
|
||||
F = |
2 m |
|
g l sin(α /2) , |
(17) |
||||||
|
||||||||||
|
τ |
|
|
|
|
|
|
|||
где τ – время соударения; α – угол отклонения ударяющего шара.
25
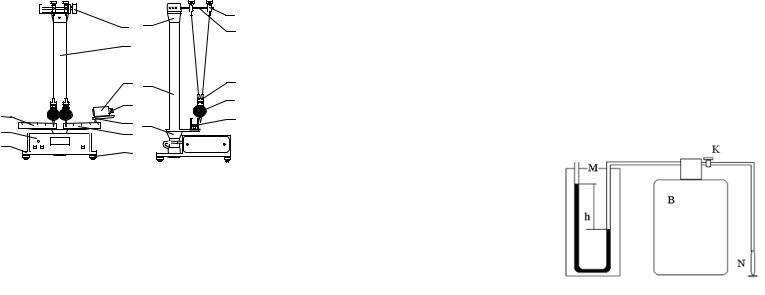
|
|
|
Описание установки |
|
|
|
|
|
|
|
8 |
|
Общий вид установ- |
||
|
7 |
5 |
6 |
ки |
для |
исследования |
|
|
|
||||||
|
3 |
|
|
столкновения шаров пред- |
|||
|
|
|
|
ставлен на рисунке 3. |
|||
|
14 |
3 |
9 |
|
В основании |
(1) с |
|
|
|
регулировочными |
ножка- |
||||
|
16 |
|
10 |
||||
11 |
|
|
ми (2) для выравнивания |
||||
15 |
|
13 |
|||||
|
4 |
установки |
закреплена ко- |
||||
17 |
|
||||||
12 |
|
|
|||||
1 |
2 |
|
|
лонка (3), |
к которой при- |
||
|
|
|
креплены |
нижний |
(4) и |
||
|
|
|
|
||||
|
Рис. 3. Внешний вид установки |
верхний (5) кронштейны. |
|||||
|
|
|
|
|
На |
верхнем |
крон- |
штейне расположены кронштейны со стержнями (6) и вороток (7), |
|||||||
служащий для установки расстояния между шарами. На стержнях рас- |
|||||||
положены держатели (8), предназначенные для крепления подвесов (9) |
|||||||
с шарами (10). |
|
|
|
|
|
|
|
|
На нижнем кронштейне закреплены угольники со шкалами (11) |
||||||
и (12), положение которых регулируется винтами (13), а на специаль- |
|||||||
ных направляющих – электромагнит (14). |
|
|
|
|
|||
|
После ослабления болтов (15) электромагнит можно передвигать |
||||||
вдоль правой шкалы и фиксировать высоту его установки. Сила элек- |
|||||||
тромагнита регулируется воротком (16). |
|
|
|
|
|||
|
На основании прибора установлен микросекундомер (17), по- |
||||||
зволяющий измерять время соударения шаров. |
|
|
|
||||
Порядок выполнения работы
1. Перед началом измерений проверьте готовность прибора к работе. При этом необходимо соблюдение следующих условий:
•шары должны чуть соприкасаться друг с другом и находиться на одном уровне;
•указатели подвесов шаров, находящихся в свободном положении, должны показывать нули на шкалах;
•электромагнит должен находиться на такой высоте, чтобы его ось была продолжением черты на шаре при его поднесении к электромагниту.
26
Из формулы (8) с учетом (5) и (6) следует:
γ = |
Cp |
= |
i+2 |
. |
(12) |
C |
i |
||||
|
V |
|
|
|
|
Эта формула показывает, что показатель адиабаты, как и теплоемкости, определяется числом степеней свободы молекул идеального газа.
Описание установки
Установка (рис.) состоит из стеклянного баллона B, закрытого пробкой, в которую вмонтированы две трубки. Одна трубка снабжена краном K, с помощью которого баллон может быть соединен либо с насосом N, либо с атмосферой. Вторая трубка соединена с манометром M. Водяной U-образный манометр измеряет разность между давлением в баллоне и атмосферным давлением в миллиметрах водяного столба. Разность между
давлением в баллоне и атмосферным измеряется по разности уровней в коленах манометра. Для определения отношения теплоемкостей Cp/CV для воздуха, находящегося в баллоне, с ним проводят последовательность термодинамических процессов, рассматриваемых ниже.
Обоснование метода
Обозначим через p0, V0, T0 начальные параметры газа в баллоне. Сначала в баллон накачивается воздух. При этом газ в баллоне сжимается и нагревается. После изохорического остывания до комнатной температуры газ имеет некоторое давление p1 = p0 + h1 и температуру T0. Затем краном соединяют баллон с атмосферой, и газ адиабатически расширяется. При этом происходит охлаждение газа, и его давление падает до величины p0, а температура − до величины T1 < T0.
В момент достижения давления p0 кран K перекрывается, и газ изохорически нагревается до комнатной температуры. В конечном состоянии давление газа p2 = p0 + h2, а температура равна T0.
83

Обычно выделяют теплоемкость при постоянном давлении (Ср), если в процессе изменения температуры тела поддерживалось постоянным давление и теплоемкость при постоянном объеме (СV) (не пу-
тать с объёмной теплоёмкостью!), если в процессе изменения тем-
пературы тела поддерживался постоянный объем.
Молярные теплоемкости при постоянном давлении и постоянном объёме определяются следующими соотношениями:
Cpµ = |
(i+2)R |
; |
(5) |
||
2 |
|
||||
|
|
|
|
|
|
C |
V µ |
= iR |
, |
|
(6) |
|
2 |
|
|
|
|
где i – число степеней свободы (число независимых координат, полностью определяющих положение молекулы в пространстве).
Связь между этими величинами выражается уравнением Майера:
Cpµ = CVµ + R. |
(7) |
Оно показывает, что Cpµ всегда больше CV µ |
на величину мо- |
лярной (универсальной) газовой постоянной R (прил. 1).
Значение теплоёмкости при постоянном давлении (Cp) сравнительно просто может быть определено из опыта, а теплоёмкость при постоянном объёме (CV) экспериментальному измерению поддается с трудом. Поэтому чаще всего сначала опытным путем находят отношение Cp/CV, а из него рассчитывают значения теплоемкостей при постоянном давлении и объеме (Cp и CV). Отношение теплоемкостей представляет собой характерную для каждого газа величину и входит в уравнение Пуассона для адиабатического процесса, поэтому получи-
ло название постоянной адиабаты (γ):
γ = Cp/CV. |
(8) |
Эту постоянную также часто называют показателем адиабаты
или коэффициентом Пуассона.
Адиабатическим процессом (адиабатным) называется процесс,
протекающий без теплообмена с окружающей средой (Q = 0). Уравнение, связывающее термодинамические параметры газа
при адиабатическом процессе, называется уравнением адиабаты, или уравнением Пуассона, в честь ученого, который впервые произвел его
вывод. Это уравнение можно записать в трех видах: |
|
pVγ = const; |
(9) |
TVγ-1 = const; |
(10) |
p1-γTγ = const. |
(11) |
82 |
|
При несоблюдении какого-либо условия обратитесь к преподавателю для регулировки установки.
2. Подготовьте таблицу для записи результатов измерений:
|
|
№ |
|
|
τ , |
p , |
|
p′, |
F , |
∆F , |
EF , |
γ , |
|||||
α , |
0 |
α′, |
0 |
|
м |
|
|
м |
|
||||||||
|
п/п |
|
10 |
−6 |
с |
кг |
|
кг |
Н |
Н |
% |
% |
|||||
|
|
|
|
|
с |
|
с |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Среднее |
|
|
|
|
|
|
|
|
|
||
3.Включите установку в сеть.
4.Отожмите кнопку «пуск», при этом включится электромагнит,
инажмите кнопку «сброс». Зафиксируйте ударяющий шар электромагнитом. Внесите значение угла α в таблицу.
5.Нажмите кнопку «пуск» и заметьте угол отклонения ударяемого шара. Запишите время соударения в таблицу, при этом индикатор перегрузки не должен светиться, в противном случае проделайте измерение заново. Проведите измерения пять раз, каждый раз записывая результаты в таблицу.
6.Выключите установку.
Обработка результатов измерений
1. Рассчитайте p , p′, F по формулам (6), (12) и (17) соответ-
ственно, внося результаты расчетов в таблицу, и найдите их средние значения. Принять m = 0,19кг и l = 0,5м.
2. По формулам EF = ∆mm + 2∆ττ + ∆aa и ∆F = EF F рассчитайте
относительную и абсолютную погрешности силы удара.
3. Рассчитайте точность выполнения закона сохранения им-
пульса по формуле γ = p −pp′ 100%.
27
4. Рассчитайте средние значения для величин p , p′, F , ∆F ,
EF , γ .
5. Результат определения средней силы удара запишите в виде:
F = (Fcp ± ∆Fcp ) Н ;
EF =...%.
6. Сделайте вывод о справедливости закона сохранения импульса.
Контрольные вопросы
1. В чем сущность метода определения средней силы удара ша-
ров?
2.Объясните явления, происходящие в процессах абсолютно упругого и абсолютно неупругого ударов.
3.Сформулируйте закон сохранения импульса.
4.Поясните способ проверки закона сохранения импульса в данной работе.
5.Запишите закон сохранения импульса упругого соударения двух тел в векторной и скалярной формах.
Лабораторная работа № 3
ПРОВЕРКА ЗАКОНА СОХРАНЕНИЯ ПОЛНОЙ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
Цель работы: проверить закон сохранения полной механической энергии.
Оборудование: автоматизированная установка «Маятник Максвелла».
Основные теоретические сведения
Энергией называется скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие. Для характеристики различных форм движения материи вводятся соответствующие виды энергии, например, механическая, внутренняя, энергия электростатических, внутриядерных взаимодействий и другие.
Механическая энергия E характеризует движение и взаимодей-
28
2.конвекция (энергия передаётся от одного тела к другому движущимися потоками жидкости или газа);
3.излучение (энергия передаётся от одного тела к другому в виде электромагнитных волн).
Теплоемкостью (С) называется количество теплоты, поглощаемое или отданное телом при изменении его температуры на 1 градус
(1°С или 1К):
C = |
|
Q |
|
. |
(1) |
T2 |
|
|
|||
|
− |
Т 1 |
|
||
Единицей измерения теплоемкости в СИ является 1 Дж/К (джоуль на кельвин).
Количество теплоты, поглощаемое или отданное телом единичной массы при изменении его температуры на 1 градус (1°С или 1К) называется удельной теплоемкостью (c) (теплоемкость единицы массы вещества). Удельная теплоемкость определяется соотношением:
c = |
Q |
|
|
(2) |
|
m (T2 − Т |
1 ) . |
||||
|
|||||
Количество теплоты, поглощаемое или отданное одним молем вещества при изменении его температуры на 1 градус (1°С или 1К)
называется молярной (мольной) теплоемкостью (Cµ). Молярная тепло-
емкость связана с удельной соотношением
C µ = c µ , |
(3) |
где µ - молярная масса вещества.
Количество теплоты, поглощаемое или отданное телом единичного объёма при изменении его температуры на 1 градус (1°С или 1К) называется объёмной теплоемкостью (cоб) (теплоемкость единицы объёма вещества). Объёмная теплоемкость определяется соотношением:
cоб = |
Q |
|
(4) |
|
V (T2 − Т1 ) . |
||||
|
||||
Единицей измерения удельной теплоемкости в СИ является 1
Дж/(кг·К) (джоуль на килограмм-кельвин), объёмной 1 Дж/(м3·К) (джоуль на кубический метр-кельвин), молярной 1 Дж/(моль·К) (джоуль на моль-кельвин).
Количество теплоты, поглощенное или отданное телом при изменении его состояния, зависит не только от начальной и конечной температур, но и от способа перехода из одного состояния в другое.
81

3. Как изменится разность показаний «сухого» и «влажного» термометров при понижении температуры, если абсолютная влажность остается неизменной?
Лабораторная работа № 12
ИЗМЕРЕНИЕ УДЕЛЬНЫХ ТЕПЛОЕМКОСТЕЙ ВОЗДУХА МЕТОДОМ КЛЕМАНА-ДЕЗОРМА
Цель работы − изучить термодинамические процессы, познакомиться с термодинамическим методом исследования, освоить классический метод измерения теплоемкостей.
Оборудование: баллон с распределительным краном, U- образный жидкостный манометр, насос.
Основные теоретические сведения
Одним из основных законов физики является закон сохранения энергии. В молекулярной физике он формулируется в виде первого начала термодинамики: количество теплоты (Q), сообщенное системе, расходуется на увеличение ее внутренней энергии ∆U и на совершение системой механической работы (A) против внешних сил:
Q = ∆U + A |
(1) |
Внутренней энергией (U ) тела называется суммарная энергия движения и взаимодействия молекул тела. Для идеального газа полагают, что молекулы между собой не взаимодействуют, следовательно, его внутренняя энергия определяется только кинетической энергией движущихся молекул.
Единицей измерения внутренней энергии в СИ является 1 Дж (джоуль).
Количество теплоты (Q) – это физическая величина, характеризующая энергию переданную или отданную телу в результате теплообмена.
Единица измерения количества теплоты в СИ: 1 Дж (джоуль)
Теплообменом называется процесс передачи энергии от одного тела к другому без совершения механической работы. Различают три вида теплообмена:
1. теплопроводность (энергия передаётся от одного тела к другому при непосредственном контакте);
80
ствие тел и является функцией скоростей и взаимного расположения тел. Полная механическая энергия равна сумме кинетической Eк и
потенциальной Ep энергий.
Кинетическая энергия определяется массами и скоростями движущихся тел (энергия движения).
При поступательном движении она определяется следующим выражением:
Ек = m2υ2 ,
где m – масса тела;
υ – скорость движения тела; При вращательном движении кинетическую энергию определя-
ют по формуле:
Eк = J 2ω2 ,
где J – момент инерции тела; ω – угловая скорость.
Моментом инерции системы (тела) относительно оси вращения называется скалярная физическая величина, равная сумме произведения элементарных масс на квадраты их расстояний до рассматриваемой оси:
n |
n |
J = ∑Ji = ∑mi ri2 . |
|
i =1 |
i =1 |
Вслучае непрерывного распределения масс эта сумма сводится
кинтегралу:
J = ∫ r2 dm = ∫ ρ r2 dV ,
(m) |
(V ) |
где ρ – плотность тела; |
|
V – объем тела; m – масса тела;
r – расстояние от оси вращения.
Для некоторых однородных тел правильной геометрической формы эти интегралы посчитаны и приведены в таблице (прил. 5).
Единица измерения момента инерции в СИ:
[J]=1кг 1м2 =1кг м2 (килограмм-квадратный метр).
Если тело участвует в нескольких видах движения, то кинетиче-
29
ская энергия суммируется.
Потенциальная энергия зависит от взаимного расположения взаимодействующих друг с другом тел (энергия положения). Вид выражения, по которому рассчитывается потенциальная энергия, зависит от вида рассматриваемого взаимодействия. Для тел, находящихся в однородном гравитационном поле Земли, потенциальная энергия определяется выражением:
Ер = m g h,
где m – масса тела;
g =9,81м/с2 – ускорение свободного падения;
h – расстояние от нулевого уровня до центра масс тела (нулевой уровень – начало отсчета – выбирается произвольно). Вследствие произвольности выбора нулевого уровня потенци-
альная энергия может принимать отрицательные значения.
Как и для любых других видов энергии единицей измерения для вышеназванных в СИ является 1Дж (джоуль).
Энергия подчиняется закону сохранения, который является одним из важнейших законов природы.
Закон сохранения энергии: полная механическая энергия тел, движущихся в поле консервативных сил, остается неизменной с течением времени. Математически это можно записать в виде:
E = const .
Консервативными называются силы, работа которых не зависит от формы траектории движения.
При наличии неконсервативных (диссипативных) сил, например, сил трения, полная механическая энергия тела не остается постоянной (часть механической энергии переходит во внутреннюю).
Обоснование метода
Проверить закон сохранения полной механической энергии можно при помощи маятника Максвелла. Он представляет собой диск, закреплённый на оси и подвешенный бифилярно на нити, способный совершать колебания в вертикальной плоскости.
Рассмотрим движение маятника подробнее. На движущийся маятник действуют консервативные силы тяжести и упругости, а также неконсервативная сила трения о воздух, которой можно пренебречь в силу её малости. В соответствии с законом сохранения, полная механиче
30
2.Осторожно, чтобы вода не попала на «сухой» термометр, смочите дистиллированной водой батист, которым обернут резервуар одного из термометров психрометра. Через 1-2 минуты после этого
произведите отсчет температур «сухого» t и «влажного» t1 термометров. Запишите результаты измерений в таблицу.
3.По барометру-анероиду определите величину атмосферного давления Н. Запишите результат измерений в таблицу (при записи учесть, что 1 мм рт. ст. = 133 Па).
Обработка результатов измерений
1.Найдите величину давления насыщенных паров pн для температуры t1 (прил. 11). Запишите результаты в таблицу.
2.Вычислите по формуле (10) относительную влажность возду-
ха для каждого опыта. Запишите результаты в таблицу.
При расчетах примите α = 0,0024 К-1.
3.Вычислите среднеарифметическое значение относительной влажности воздуха. Запишите результаты в таблицу.
4.Оцените абсолютную (∆r) и относительную (Еr) погрешности измерений влажности воздуха методом среднего значения.
5.Запишите конечный результат в виде:
r = (rср ±∆rср)%;
Еr =...%.
6.Определите величину относительной влажности воздуха по психрометрической таблице (прил. 12).
7.Сравните значение относительной влажности воздуха r, рассчитанное по формуле (10) и определенное по психрометрической таблице.
8.Сделайте вывод о причинах несовпадения результатов.
Контрольные вопросы
1.Что называется абсолютной и относительной влажностью воздуха? В каких единицах они измеряются?
2.Для чего нужно измерять влажность воздуха в сельском хозяйстве и других отраслях производства?
79
