II. Выполнение эксперимента и обработка результатов испытаний

1. Зарисовать расчетную схему балки.

2. Собрать установку согласно расчетной схеме.

3. Снять необходимые размеры балки.

4. Собрать штатив с индикатором, установить стрелку индикатора на «0».

5. Нагрузить балку.

6. С помощью индикатора измерить прогиб в точке , где предполагается наличие «лишней» опоры.

7. Подсчитать значение реакции «лишней» опоры в точке.

8. Приложить к балке в точке силу, равную подсчитанной величине.

9. Снять показания индикатора повторно*.

10. Подсчитать расхождение экспериментального и теоретического значений реакции по формуле (5).

11. Сделать выводы о достоверности метода сил.

* Если значение реакции найдено верно, то стрелка индикатора вернется в нулевое положение.

III. Вопросы для подготовки к защите работы:

1. В чем заключается раскрытие статической неопределимости балки методом сил?

2. В чем отличие метода сил от метода сравнения деформаций?

3. Как найти значения коэффициентов канонических уравнений?

4. Как найти значения свободных членов канонических уравнений?

5. Что такое единичное перемещение?

ЛАБОРАТОРНАЯ РАБОТА № 5

Тема: Косой изгиб.

Цель работы:

Проверить экспериментальные расчеты напряжений и значений прогиба в балке при косом изгибе.

Необходимое оборудование и приборы

1. Консольная стальная балка прямоугольного поперечного сечения.

2. Тензометр.

3. Индикатор - прибор для измерения линейных перемещений точек (прогибов балки).

4. Штатив для крепления индикатора.

5. Подвеска с грузом.

6. Штангенциркуль.

I. Теоретические основы работы

Косым называется такой изгиб, при котором плоскость действия изгибающего момента не совпадает ни с одной из главных осей инерции сечение сечения (рис. 1).

Рисунок 1. Косой изгиб.

На рис 1. угол обозначает положение нейтральной линии, угол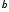− положение линии по которой перемещается центр тяжести поперечного сечения, угол− положение линии действия силы.

Напряжения при косом изгибе определяются по формулам:

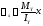, , (6)

где ,− изгибающие моменты относительно осей главных осей,;

, − главные моменты инерции ;

, − координаты той точки поперечного сечения, в которой определяется напряжение.

Прогиб при косом изгибе определяется по формуле:

, (7)

где ,− прогибы балки вдоль главных осей инерции.

II. Выполнение эксперимента и обработка результатов испытаний

1. Зарисовать расчетную схему балки.

2. Собрать установку согласно расчетной схеме.

3. Снять необходимые размеры балки.

4. Установить тензометры и индикаторы.

5. Нагрузить балку.

6. Снять показания индикаторов и тензометров и занести их в отчет.

7. Определить значения напряжений и перемещений балки любым известным способом.

8. Подсчитать расхождение экспериментальных и теоретических значений перемещений по формуле (2), а напряжений по следующей формуле:

(8)

9. Сделать выводы.

III. Вопросы для подготовки к защите работы:

1. Что такое косой изгиб?

2. Почему балки с квадратным и круглым поперечным сечением не испытывают косого изгиба?

3. Для чего и как определяется положение нейтральной линии при косом изгибе?

4. Как определяется положение линии перемещения центра тяжести поперечного сечения при косом изгибе?

5. Как найти опасные точки при косом изгибе?

6. Записать условие прочности при косом изгибе.

ЛАБОРАТОРНАЯ РАБОТА № 6

Тема: Внецентренное растяжение.

Цель работы:

Опытная проверка расчетных значений напряжений в поперечном сечении стержня при внецентренном растяжении.

Необходимые приборы и оборудование

1. Образец стальной прямоугольного поперечного сечения.

2. Тензометр.

3. Штангенциркуль.

4. Универсальная машина УМ – 5.