
- •Acknowledgments
- •About the Author
- •1.1 Basic Computer Structure
- •1.3 A Few Instructions and Some Simple Programs
- •2 The Instruction Set
- •3.1 Op Code Byte Addressing Modes
- •4.2 Assembler Directives
- •4.3 Mechanics of a Two-Pass Assembler
- •4.6 Summary
- •5.1 Cross Assemblers and Downloaders
- •5 Problems
- •6.3 Passing Arguments by Value, Reference, and Name
- •7 Arithmetic Operations
- •7.2 Integer Conversion
- •8 Programming in C and C++
- •8.1 Compilers and Interpreters
- •9 Implementation of C Procedures
- •9.2 Expressions and Assignment Statements
- •9.4 Loop Statements, Arrays, and Structs
- •10 Elementary Data Structures
- •10.1 What a Data Structure Is
- •11.4 Synchronization Hardware
- •12.4 The 68300 Series
- •A2.1 Loading HiWare Software
- •A2.2 Opening the HiWare Toolbox
- •A2.3 Running Examples From the ManualProgramFolder
- •A2.6 POD-Mode BDM Interface
- •Index

7.2 |
Integer Conversion |
183 |
* |
SGNMUL multiplies the 1-byte signed number in B by the 1-byte signed number in |
|
* |
||
* |
A, putting the product in accumulator D. Registers X and Y are unchanged. |
|
* |
|
|
SGNMUL: |
PSHD |
|
; Save two bytes to be multiplied |
|
|
|
MUL |
|
; Execute unsigned multiplication |
|
|
TST |
1, SP |
; If first number is negative |
|
|
BPL |
LI |
; Then |
|
|
SUBA |
0, SP |
; Subtract second number |
LI: |
|
TST |
0,SP |
;If second number is negative |
|
|
BPL |
L2 |
; Then |
|
|
SUBA |
1, SP |
; Subtract first number |
L2: |
|
LEAS |
2, SP |
; Balance stack |
|
|
RTS |
|
; Return with product in accumulator D |
|
|
|
|
a. Using MUL |
* |
|
|
|
|
* |
SGNMUL multiplies the 1-byte signed number in B by the 1-byte signed number in |
|||
* |
A, putting the product in accumulator D. Register X is unchanged. |
|||
* |
|
|
|
|
SGNMUL: |
SEX |
A, Y |
; move one multiplier to Y, sign extending it |
|
|
|
SEX |
Bf D |
; sign extend the other multiplier |
|
|
EMULS |
|
; put the low-order 16-bits in D |
|
|
RTS |
|
; Return with product in accumulator D |
b. Using EMULS
Figure 73.8-Bit Signed Multiply Subroutine
Another approach to multiplication of signed 8-bit numbers is to use signed 16-bit multiplication available in the EMULS instruction. See Figure 7.3b. This method is far better on the 6812, because the EMULS instruction is available, but the former method is useful on other machines and shows how signed multiplication is derived from unsigned multiplication having the same precision. A modification of it is used to multiply 32-bit signed numbers, using a procedure to multiply 32-bit unsigned numbers.
7.2 Integer Conversion
A microcomputer frequently communicates with the outside world through ASCII characters. For example, subroutines INCH and DUTCH allow the MPU to communicate with a terminal, and this communication is done with ASCII characters. When numbers are being transferred between the MPU and a terminal, they are almost always decimal numbers. For example, one may input the number 3275 from the terminal keyboard, using the subroutine INCH, and store these four ASCII decimal digits in a buffer. After the digits are input, the contents of the buffer would be

184 |
Chapter 7 Arithmetic Operations |
While each decimal digit can be converted to binary by subtracting $30 from its ASCII representation, the number 3275 still has to be converted to binary (e.g., $OCCB) or some other representation if any numerical computation is to be done with it. One also has to convert a binary number into an equivalent ASCII decimal sequence if this number is to be displayed on the terminal screen. For example, suppose that the result of some arithmetic computation is placed in accumulator D, say, $OCCB. The equivalent decimal number, in this case 3275, must be found and each digit converted to ASCII before the result can be displayed on the terminal screen. We focus on the ways of doing these conversions in this section.
One possibility is to do all of the arithmetic computations with binary-coded decimal (BCD) numbers, where two decimal digits are stored per byte. For example, the BCD representation of 3275 in memory would be
Going between the ASCII decimal representation of a number to or from equivalent BCD representation is quite simple, involving only shifts and the AND operation. With the 6812, it is a simple matter to add BCD numbers; use ADDA or ADCA with the DAA instruction. Subtraction of BCD numbers on the 6812 must be handled differently from the decimal adjust approach because the subtract instructions do not correctly set the halfcarry bit H in the CC register. (See the problems at the end of the chapter.) For some applications, addition and subtraction may be all that is needed, so that one may prefer to use just BCD addition and subtraction. There are many other situations, however, that require more complex calculations, particularly applications involving control or scientific algorithms. For these, the ASCII decimal numbers are converted to binary because binary multiplication and division are much more efficient than multiplication and division with BCD numbers. Thus we convert the input ASCII decimal numbers to binary when we are preparing to multiply and divide efficiently. However, depending on the MPU and the application, BCD arithmetic may be adequate so that the conversion routines below are not needed.
We consider unsigned integer conversion first, discussing the general idea and then giving conversion examples between decimal and binary representations. A brief discussion of conversion of signed integers concludes this section. The conversion of numbers with a fractional part is taken up in a later section.
An unsigned integer N less than bm has a uniquerepresentation





7,2 Integer Conversion |
189 |
*CVBTD converts the unsigned contents of D into an equivalent 5-digit ASCII decimal
*number ending at the location passed in X. Register Y is unchanged.
*
CVBTD: |
PSHX |
|
; Save beginning address of string |
|
LEAK |
5, X |
; End address of string |
|
PSHX |
|
; Save on stack |
LI: |
LDX |
#10 |
; Divide by 10 |
|
LDY |
#0 |
; High 16-bits of dividend (low 16-bits in D) |
|
EDIV |
|
; D is remainder Y is quotient |
|
ADDB |
#$30 |
; ASCII conversion |
|
PULX |
|
; Restore output string pointer |
|
STAB |
1r -X |
; Store character, move pointer |
|
PSHX |
|
; Save output string pointer |
|
XGDY |
|
; Remainder to D |
|
CPX |
2 ,SP |
; At end of string? |
|
BNE |
LI |
; Continue |
|
LEAS |
4, SP |
; Balance stack |
|
RTS |
|
; Exit |
a.Using a Loop
*SUBROUTINE CVBTD converts unsigned binary number in D into five
*ASCII decimal digits ending at the location passed in X, using recursion.
*
CVBTD: |
PSHX |
|
; Save string pointer |
|
LDY |
#0 |
; High dividend |
|
LDX |
#10 |
; Divisor |
|
EDIV |
|
; Unsigned (Y:D) / X -> Y, remainder to D |
|
ADDB |
#$30 |
; Convert remainder to ASCII |
|
PULX |
|
; Get string pointer |
|
STAB |
1, -X |
; Store in string |
|
TFR |
Y, D |
; Put quotient in D |
|
TBEQ |
D, LI |
; If zero, just exit |
|
BSR |
CVBTD |
; Convert quotient to decimal (recursively) |
LI: |
RTS |
|
; Return |
b. UsingRecursion
Figure 7.8 Conversion from Binary to Decimal by Division by 10
Looking at the expansion (3) we see that N4 is the quotient of the division of (D) by (K):(K + 1). If we divide the remainder by (K + 2):(K+ 3), we get N3 for the quotient, and so forth. These quotients are all in binary, so that a conversion to ASCII is also necessary. The subroutine CVBTD of Figure 7.6 essentially uses this technique, except that the division is carried out by subtracting the largest possible multiple of each power of ten which does not result in a carry.





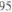
7,3 From Formulas to SubroutineCalls |
195 |
Figure 7.13. Algorithm to Write a Sequence of Subroutine Calls for (8)
The reader is invited to find these parsing trees for the formulas given in the problems at the end of the chapter. Note that a parsing tree is really a good way to write a formula because you can see "what plugs into what" better than if you write the formula in the normal way. In fact, some people use these trees as a way to write all of their formulas,even if they are not writing programs as you are, because it is easier to spot mistakes and to understand the expression. Once the parsing tree is found, we can write the sequence of subroutine calls in the following way. Draw a string around the tree, as shown in Figure 7.13. As we follow the string around the tree, a subroutine call or PUSH is made each time we pass a node for the last time or, equivalently, pass the node on the right. When a node with an operand is passed, we execute the macro PUSH for that operand. When a node for an operation is passed, we execute a subroutine call for that operation. Compilers use parsing trees to generate the subroutine calls to evaluate expressions in high-level languages. The problems at the end of the chapter give you an opportunity to learn how you can store parsing trees the way that a compiler might do it, using techniques from the end of Chapter 6, and how you can use such a tree to write the sequence of subroutinecalls the way a compiler might.
As a second example, we consider a program evaluatingthe consecutive expressions
delta = delta + c
s = s + (delta *delta) These can be described by the trees


7,4 Long Integer Arithmetic |
197 |
|
PSHD |
|
; Move up low 16-bits from register L to stack |
PSHY |
|
; Move up high 16-bits from register L to stack |
LDY |
ALPHA |
; Get high 16-bits of register L |
LDD |
ALPHA+2 |
; Get low 16-bits of register L |
This program segment's first two instructions alone will duplicate the top stack element,
PSHD |
; Duplicate low 16-bits from register L to stack |
PSHY |
; Duplicate high 16-bits from register L to stack |
Similarly, to maintain the stack mechanism, a long word can be pulled from the stack to fill L. The following program segment pulls a long word into location ALPHA.
STY |
ALPHA |
; Save high 16-bits of register L |
STD |
ALPHA+2 |
; Save low 16-bits of register L |
PULY |
|
; Move down high 16-bits to register L |
PULD |
|
; Move down low 16-bits to register L |
If you use a macro assembler, these operations are easily made into macros. Otherwise, you can "hand-expand" these "macros" whenever you need these operations.
A 32-bit negate subroutine is shown in Figure 7.14. The algorithm is implemented by subtracting register L from 0, putting the result in L. This is a monadic operation, an operation on one operand. You are invited to write subroutines for other simple monadic operations. Increment and decrement are somewhat similar, and shift left and right are much simpler than this subroutine. (See the problems at the end of the chapter.)
A multiple-precision comparison is tricky in almost all microcomputers if you want to correctly set all of the condition code bits so that, in particular, all of the conditional branch instructions will work after the comparison. The subroutine of Figure 7.15 shows
how this can be done for the 6812. |
If Z is initially set, using ORCC #4, entry at |
||
CPZRO |
will test register L for zero while pulling it from the stack. The first part of this |
||
subroutine suggests |
how subroutines for addition, subtraction, ANDing, ORing, and |
||
exclusive-ORing can be written. |
|
||
* |
SUBROUTINE NEG negates the 32-bit number in L. |
||
* |
|
|
|
NEG: |
PSHY |
|
; Save high 16 bits |
|
PSHD |
|
; Save low 16 bits, which are used first |
|
CLRA |
|
; Clear accumulator D |
|
CLRB |
|
|
|
SUED |
2 ,SP+ |
; Pull low 16 bits, subtract from zero |
|
TFR |
D, Y |
; Save temporarily in Y |
|
LDD |
#0 |
; Clear accumulator D, without changing carry |
|
SBCB |
1, SP |
; Subtract next-to-most-significant byte |
|
SBCA |
2 ,SP+ |
; Subtract most-significant byte, balance stack |
|
XGDY |
|
; Exchange temporarily in Y with high 16-bits |
|
RTS |
|
; Return with result in register L |
Figure 7.14.32-Bit Negation Subroutine


7.4 Long Integer Arithmetic |
199 |
*SUBROUTINE MULT multiplies the unsigned next word on the stack with
*L, and pulls the next word
sK
LCSAVE: |
EQU |
* |
|
|
ORG |
0 |
|
PROD: |
DS.L |
1 |
|
N: |
DS.L |
1 |
|
M: |
DS.L |
1 |
|
|
ORG |
LCSAVE |
|
MULT: |
PULX |
|
; pull return address |
|
PSHD |
|
; low part of N |
* |
PSHY |
|
; high part of N |
|
|
|
|
|
LDY |
M+2 - 4, SP |
; note: M is operand offset in sub middle |
|
EMUL |
|
; note - accum D is still low part of N |
|
PSHD |
|
; low word of product |
* |
PSHY |
|
; high word of product |
|
|
|
|
|
LDD |
N, SP |
; get high part of N |
|
LDY |
M+2, SP |
; get low part of M |
|
EMUL |
|
|
|
ADDD |
PROD, SP |
; add to high word |
* |
STD |
PRODr SP |
; place back |
|
|
|
|
|
LDD |
N+2, SP |
; get low part of N |
|
LDY |
M, SP |
; get high part of M |
|
EMUL |
|
|
|
ADDD |
PROD, SP |
; add to high word |
|
TFR |
D,Y |
; high 16 bits |
* |
LDD |
PROD+2 , SP |
; low 16 bits |
|
|
|
|
|
LEAS |
12, SP |
; remove M, N, and PROD |
|
JMP |
0, X |
; return |
|
Figure 7.17.32-Bit by 32-Bit Unsigned Multiply Subroutine |
||
LCSAVE: |
EQU |
* |
|
|
ORG |
0 |
|
RTRN: |
DS.W |
1 |
|
COUNT: |
DS.B |
1 |
|
DVS: |
DS.L |
1 |
|
REM: |
DS.L |
1 |
|
QUOT: |
DS.L |
1 |
|
Figure 7.18. 32-Bit by 32-Bit Unsigned Divide Subroutine

200 |
Chapter 7 ArithmeticOperations |
ORG LCSAVE
*
*SUBROUTINE DIV
*DIV divides the unsigned next word on the stack into L, and pulls the next word
DIV: |
PULX |
|
; unstack return address |
|
LEAS |
- 4 ,SP |
; room for remainder right above dividend |
|
PSHD |
|
; save low 16 bits of divisor |
|
PSHY |
|
; save high 16 bits of divisor |
|
MOVB |
#32,1, -SP |
; count for 32 bits |
|
PSHX |
|
; put back return address |
|
CLRA |
|
|
|
CLRB |
|
|
|
STD |
REM,SP |
|
* |
STD |
REM+2,SP |
|
|
|
|
|
DIV1: |
CLC |
|
; divide loop |
|
LDAA |
#8 |
; shift remainder and divisor: shift 8 bytes |
|
LEAK |
QUOT+3, SP |
; pointer for bottom of quotient-remainder |
DIV2: |
ROL |
1, X- |
|
* |
DBNE |
A,DIV2 |
|
|
|
|
|
|
LDY |
REM, SP |
; subtract from partial product |
|
LDD |
REM+2 , SP |
; (note: 4 extra bytes on stack) |
*
|
SUED |
DVS+2,SP |
|
|
XGDY |
|
|
|
SBCB |
DVS+1,SP |
|
|
SBCA |
DVS,SP |
|
* |
XGDY |
|
|
|
|
|
|
|
BCS |
DIV3 |
; if borrow |
|
STD |
REM+2 , SP |
; then put it back |
|
STY |
REM,SP |
|
|
INC |
QUOT+3, SP |
; and put 1 into Isb of quotient |
DIV3: |
DEC |
COUNT, SP |
; counter is high byte of last operand |
* |
BNE |
DIV1 |
; count down - 32 bits collected |
|
|
|
|
|
PULX |
|
; pull return |
|
LEAS |
9 ,SP |
;balance stack - remove divisor |
|
PULY |
|
|
|
PULD |
|
; pop quotient |
DIVEXIT: |
JMP |
0,X |
; return to caller |
Figure 7.18. Continued.




204 |
Chapter 7 Arithmetic Operations |
24 * 1.00 . . . 0
+22 * 1.00 . . . 0
we first unnormalize the number with the smaller exponent and then add as shown,
24 * 1.000 .. . 0
+24 * 0.010 . . . 0
24 * 1.010 .. . 0
(For this example and all those that follow, we give the value of the exponent in decimal and the 24-bit magnitude of the significand in binary.) Sometimes, as in adding,
24 |
* |
1.00 |
. . . 0 |
+ 24 |
* |
1.00 |
. . . 0 |
24 |
*10.00 |
. . . 0 |
|
the sum will have to be renormalized before it is used elsewhere. In this example
25 * 1.00 . . . 0
is the renormalization step. Notice that the unnormalization process consists of repeatedly shifting the magnitude of the significand right one bit and incrementing the exponent until the two exponents are equal. The renormalization process after addition or subtraction may also require several steps of shifting the magnitude of the significand left and decrementing the exponent. For example,
24 * 1.0010 .. . 0
-24 * 1.0000 . . .0
24 * 0.0010 .. . 0
requires three left shifts of the significand magnitude and three decrements of the exponent to get the normalized result:
21 * 1.00 . . . 0
With multiplication, the exponents are added and the significands are multiplied to get the product. For normalized numbers, the product of the significands is always less than 4, so that one renormalization step may be required. The step in this case consists of shifting the magnitude of the significand right one bit and incrementing the exponent. With division, the significands are divided and the exponents are subtracted. With normalized numbers, the quotient may require one renormalization step of shifting the magnitude of the significand left one bit and decrementing the exponent. This step is required only when the magnitude of the divisor significand is larger than the magnitude of the dividend significand. With multiplication or division it must be remembered also that the exponents are biased by 127 so that the sum or difference of the exponents must be rebiased to get the proper biased representation of the resulting exponent.
7,5 Floating-Point Arithmetic and Conversion |
205 |
In all of the preceding examples, the calculations were exact in the sense that the operation between two normalized floating-point numbers yielded a normalized floatingpoint number. This will not always be the case, as we can get overflow, underflow, or a result that requires some type of rounding to get a normalized approximation to the result. For example, multiplying
256 * i.oo . . . 0
*210Q * 1.00 . . . 0
2*56 * 1.00 . . . 0
yields a number that is too large to be represented in the 32-bit floating-point format. This is an example of overflow, a condition analogous to that encountered with integer arithmetic. Unlike integer arithmetic, however, underflow can occur, that is, we can get a result that is too small to be represented as a normalized floating-point number. For example,
2-126 * 1.0010 . . . 0
-2-l26 * 1.0000 . . . 0 2-126 * 0.0010 . . . 0
yields a result that is too small to be represented as a normalized floating-point number with the 32-bit format.
The third situation is encountered when we obtain a result that is within the normalized floating-point range but is not exactly equal to one of the numbers (14). Before this result can be used further, it will have to be approximated by a normalized floating-point number. Consider the addition of the following two numbers.
22 |
* |
1.00 |
. . . 00 |
+ 20 * |
1.00 |
. . . 01 |
|
22 |
* 1.01 |
. . . 00(01) |
|
(in parenthesis: least significant bits of the significand)
The exact result is expressed with 25 bits in the fractional part of the significand so that we have to decide which of the possible normalized floating-point numbers will be chosen to approximate the result. Rounding toward plus infinity always takes the approximate result to be the next larger normalized number to the exact result, while rounding toward minus infinity always takes the next smaller normalized number to approximate the exact result. Truncation just throws away all the bits in the exact result beyond those used in the normalized significand. Truncation rounds toward plus infinity for negative results and rounds toward minus infinity for positive results. For this reason, truncation is also called rounding toward zero. For most applications, however, picking the closest normalized floating-point number to the actual result is preferred. This is called rounding to nearest. In the case of a tie, the normalized floating-point number with the least significant bit of 0 is taken to be the approximate result. Rounding to nearest is the default type of rounding for the IEEE floating-point standard. With rounding to nearest, the magnitude of the error in the approximate result is less than or equal to the magnitude of the exact result times 2~24.

206 |
Chapter 7 Arithmetic Operations |
One could also handle underflows in the same way that one handles rounding.For example, the result of the subtraction
2-126 * i . oilO . . . 0
-2-126 * i.oooo . . . Q 2-126 * 0.0110 . . . 0
could be put equal to 0, and the result of the subtraction
2-126 * |
i.ioiO |
. . . 0 |
||
2-126 |
* i.oooo |
. . . |
Q |
|
2-126 |
* |
0.1010 |
. . . |
0 |
could be put equal to 2~126 * 1.0000. More frequently,all underflow results are put equal to 0 regardless of the rounding method used for the other numbers. This is termed flushing to zero. The use of denormalized floating-point numbers appears natural here, as it allows for a gradual underflow as opposed to, say, flushing to zero. To see the advantage of using denormalized floating-point numbers, consider the computation of the expression (Y — X) + X. I f Y - X underflows, X will always be the computed result if flushing to zero is used. On the other hand, the computed result will always be Y if denormalized floating-point numbers are used. The references mentioned at the end of the chapter contain further discussions on the merits of using denormalized floating point numbers. Implementing all of the arithmetic functions with normalized and denormalized floating-point numbers requires additional care, particularly with multiplication and division, to ensure that the computed result is the closest represented number, normalized or denormalized, to the exact result. It should be mentioned that the IEEE standard requires that a warning be given to the user when a denormalized result occurs. The
motivation for this is that one is losing precision with denormalized |
floating-point |
||||
numbers. For example, if during the calculation of the expression |
(Y |
— |
X) |
* |
Z. If Y |
-X underflows, the precision of the result may be doubtful even if |
(Y |
— |
X) |
* |
Zisa |
normalized floating-point number. Flushing to zero would, of course, always produce zero for this expression when (Y — X) underflows.
The process of rounding to nearest, hereafter just called rounding, is straightforward after multiplication. However, it is not so apparent what to do after addition, subtraction, or division. We consider addition/subtraction. Suppose, then, that we add the two numbers
20 * 1.0000 . . . 0
+2-23 * 1.1110 . . . 0
After unnormalizing the second number,we have
20 * 1.0000 .. . 00
+2° * 0.0000 . . . Qlflll) 20 * 1.0000 . . . 01(111)

7.5 Floating-Point Arithmetic and Conversion |
207 |
(The enclosed bits are the bits beyond the 23 fractional bits of the significand.) The result, when rounded, yields 2° * 1.0 . . . 010. Byexamining a number ofcases, one can see that only three bits need to be kept in the unnormalization process,namely,
where g is the guard bit, r is the round bit, and s is the sticky bit. When a bit b is shifted out of the significand in the unnormalizationprocess. 
Notice that if s ever becomes equal to 1 in the unnormalization process, it stays equal to 1 thereafter or "sticks" to 1. With these three bits, rounding is accomplished by incrementing the result by 1 if
or
If adding the significands or rounding causes an overflow in the significand bits (only one of these can occur), a renormalization step is required. For example,
2° * 1.1111 . . . 1
+2-23 * Lino . . . 0
becomes, after rounding, 2° * 10.0 . . . 0 Renormalization yields 2l * 1.0
. . . 0, which is thecorrect rounded result, and no further rounding is necessary. Actually, it is just as easy to save one byte for rounding as it is to save three bits,
so that one can use six rounding bits instead of one, as follows.
The appropriate generalization of (15) can be pictured as
while (16) is exactly the same as before with r replaced by 15 ... TO









216 |
Chapter 7 Arithmetic Operations |
Do You Know These Terms?
See the end of chapter 1 for instructions.
long data |
floating-point |
rounding toward |
fuzzy inference |
float data |
numbers |
zero |
kernel |
state |
bias |
rounding to |
knowledge base |
biasing |
normalized |
nearest |
antecedent |
rn-digit base-b |
number |
flushing to zero |
fuzzy AND |
representation |
denormalized |
rounding |
consequent |
Polish notation |
number |
guard bit |
fuzzy OR |
parsing tree |
unnormalization |
round bit |
fuzzy negate |
fixed-point |
renormalized |
sticky bit |
singleton |
representation |
overflow |
decimal floating- |
|
significand |
underflow |
point number |
|
exponential part |
rounding toward |
linguistic variable |
|
floating-point |
plus infinity |
value |
|
hidden bit |
rounding toward |
membership |
|
single precision |
minus infinity |
function |
|
floating-point |
truncation |
rule |
|




