
Ларионов - Методы измерения физических величин. Учебное пособие - 2005
.pdfФ Е Д Е РАЛ Ь Н О Е АГ Е Н С ТВ О П О О БРАЗО |
В АН И Ю |
В О РО Н Е Ж С КИ Й Г О С У Д АРС В Е Н Н Ы Й У Н И |
В Е РС И ТЕ Т |
Л |
а рион ов А .Н ., |
Ч |
е рн ы ш ëв В .В ., |
Л |
а рион ов а Н .Н . |
М Е Т О Д Ы ИЗМ Е РЕ Н ИЯ ФИЗИЧ Е СК ИХ В Е Л ИЧ ИН
У Ч Е БНО Е П О СО |
БИ Е |
|
поспециальностям: |
||
ф и зи ка |
010701 |
(010400) |
м и кроэлектрони ка и |
|
|
полупроводни ковыепри боры |
010803 |
(014100) |
ради оф и зи ка и электрони ка |
010801 |
(013800) |
ВО РО Н Е Ж
2005
2
У твержденонаучно-методическим советом физическог офакультета 2005 г . протокол№ 5
Авторы : Л арионовА.Н .,
Черны ш ëвВ .В .,
Ларионова Н .Н .
Учебное пособие подготовленона кафедре общ ей физикифизическог офакультета В оронежског огосударственног оуниверситета.
Рекомендуется для студентов физическог о факультета специальностей: 010701 (физика), 010803 (микроэлектроника ифизика полупроводников), 4 курса дневной формы обучения, специальности 010801 (радиофизика и электроника) 2 курса вечерней формы обучения.
3
ВВ Е Д Е Н И Е
Клинейны м компонентам электрических и радиотехнических цепей с сосредоточенны ми параметрами относятрезисторы , конденсаторы и индуктивны е катуш ки. О сновны ми параметрами их являю тсясоответственно активное сопротивление (R), индуктивность (L) и емкость (С). В больш инстве случаевизмерять
эти параметры можно путем сравнения с соответствую щ ими образцовы ми элементами – мерами, которы е вы полняю тввиде декадны х маг азиновR, L или С, иног да снабжаемы х переменны ми резисторами, вариометрами или воздуш ны ми конденсаторами дляустановленияпромежуточны х значений этих величин. Кажды й маг азинхарактеризуетсяопределенны м значением какосновной погреш ности при нормальны х условиях эксперимента, таки дополнительны ми погреш ностями, вы зы ваемы ми, например, влиянием поверхностног о эффекта, наличием индуктивности упроволочны х резисторов, междувитковы х емкостей уобразцовы х индуктивностей.
П ри вы полнении точны х измерений необходимо учиты вать возможность появленияэтих погреш ностей икомпенсироватьих влияниена результатизмерениявведением поправокилиприменением друг ог ометода измерения.
М етоды измерениясопротивления, индуктивностииемкостиможноразде-
лить на три г руппы : 1) с помощ ью ам перметра и вольтметра; 2) мостовой м е-
тод, при котором измеряемое активное и реактивное сопротивление сравниваю т с сопротивлениями рабочих элементов, вклю ченны х в соответствую щ ие плечи мостовой схемы ; 3) резонансный метод, ког да измеренияпроизводятпри резонансной настройке измерительной схемы , вы полненной в виде колебательног о контура.
В ы бор метода измеренияопределяетсятребуемой точностью идиапазоном
частот, в котором должны работать исследуемы е компоненты |
схемы . В частно- |
сти, на вы соких частотах необходимо учиты вать собственную |
емкость катуш ек |
индуктивностиипараметры измерительной схемы , которы е принизких частотах не иг раю тсущ ественной роли. Кажды й из перечисленны х методовможно сочетатьсметодом замещ ениядляполученияболееточны х результатов.
1. И ЗМ Е РЕ Н И Е С О П РО ТИ В Л Е Н И Я С П О М О Щ Ь Ю АМ П Е РМ Е ТРА И В О Л Ь ТМ Е ТРА
С опротивления относятся к числу важнейш их параметров электронны х устройств. В практике измерений возникаетнеобходимость определениясопротивлений от10-8 до1016 О м . У словносопротивленияделятна триг руппы : малы е
– до 1 О м , средние – от1 О м до105 О м ибольш ие – свы ш е 105 О м . В ы борметода и средства измерениясопротивлениявкаждом конкретном случае зависит отзначениясопротивления, требований кточностииотусловий измерений.
4
М етод амперметра и вольтметра являетсяодним из наиболеепросты х, но ине менее точны х методовизмерениясопротивления. О нзаклю чаетсявизмерениитока илинапряжения, функциональносвязанног осизмеряемы м сопротивлением, иоснованна применениизакона О ма.
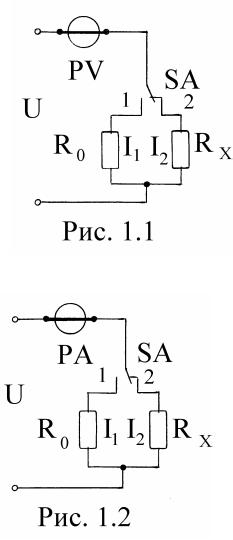
1.1.С хема содним вольтметром
Всхеме содним вольтметром (рис.1.1) при неизменном напряжениипи-
таниявположении1 переклю чателяSA (R0= =0) приборпоказы ваетнапряжение
U1= !1·Rv= =(U/Rv)·Rv=U,
а в положении 2 переклю чателя SA – напряжение:
U2=I2·Rv=U·Rv /(Rv+Rx ).
Здесь U1=U, то есть U2=U1·Rv /(Rv+Rx ),
следовательно U2·Rv+U2·Rx=U1·Rv.
Таким образом, неизвестное сопротивление рассчиты ваю т по двум показаниям вольтметра: U1 и U2 и по ег о входному сопротивлению :
Rx=Rv·[(U1 /U2 )–1].
1.2. С хема содним амперметром
В схеме с одним амперметром (рис.1.2) в положении 1 переклю чателя SA показание амперметра пропорциональносилетока:
I1= U/(R0+RA ),
а вположении2 переклю чателяSA:
I2 = U/(Rx+RA ).
Реш ениеполученной системы двух уравнений позволяетвы разитьнеизвестноесопротивление:
Rx=(I1 /I2)·(R0+RA )-RA.
1.3.С хема самперметром ивольтметром
При известном входном сопротивлении используемы х приборовнеизвест-
ноесопротивление Rx приположении1 переклю чателяSA рассчиты ваю тпоформуле:
R’ = (U /I )-R .
x v A A
О тносительнаяпогреш ностьприэтом непревы ш аетзначения:
δ’=(RA /Rx )·100%.

5
В положении 2 переклю чателя SA неизвестноесопротивлениерассчиты ваю тпо формуле:
R”x=Uv /[IA-(Uv /Rv )],
а погреш ность измерения сопротивления не превы ш аетзначения:
δ”=-Rx /(Rx –Rv )·100%.
П риведенны е формулы показы ваю т, что схемы вклю чения амперметра и вольтметра (рис.1.3) приположениях 1 и2 переклю чателя SA неравноценны . Э то объ ясняется тем, что вольтметр, вклю ченны й до амперметра при положении 1 переклю чателя SA, показы вает суммарное падение напряженияна амперметре
и на измеряемом сопротивлении. П оэтому результаты измерений превы ш аю т действительноезначениесопротивления.
П ри положении 2 переклю чателя SA амперметр показы вает силу тока, больш ую действительной на значениесилы тока, протекаю щ ег очерез вольтметр.
Таким образом, при известном входном сопротивлении приборов можно использоватьлю бую из рассмотренны х схем дляопределениязначенияRx .
Е сли сопротивления приборов неизвестны , то дляопределения малы х сопротивлений измерения целесообразно производить при положении 2 переклю - чателяSA; а дляопределениясредних сопротивлений измеренияследуетпроизводитьприположении1 переклю чателяSА.
2. И ЗМ Е РЕ Н И Е БО Л Ь Ш И Х С О П РО ТИ В Л Е Н И Й
Больш ие сопротивленияможноизмерить, исследуяпроцессзаряда конденсатора через объ ектснеизвестны м сопротивлением Rx споследую щ им измерени-
ем |
накопленног о |
в |
конденсаторе С заряда |
Q за |
|
время t. Д ля вы полне-ния измерений переклю чатель SA на время t устанавливаю т в положение 1 (рис.2.1). За это время конденсатор С получает количество электричества
Q=U·C·{1 – exp[-t/(Rx·C)]}.
Затем переклю чатель SA переводятвположение2.
6
П ервоемаксимальноеотклонениебаллистическог ог альванометра равно:
α1m=Q/CQ ,
г де CQ – баллистическаяпостояннаяг альванометра. С ледовательноCQ·α1m=Q, то есть
CQ·α1m = U·C·{1 –exp[-t/(Rx·C)]}.
Таким образом,
CQ·α1m= U·C - U·C·exp[-t/(Rx·C)];
exp[-t/(Rx·C)] = 1 - CQ·α1m / U·C;
-t/(Rx·C) = ln[(U·С - CQ·α1m )/ U·С];
окончательно:
Rx·= (t/C)·ln[U·С/(U·С - CQ·α1m )],
или
Rx·≈(t·U)/( CQ·α1m)
при
t·« Rx·C.
Д ля вы полнения измерений таким способом требуется конденсатор с хорош им сопротивлением изоляции.
Рассмотренны е вы ш е косвенны е методы измерения сопротивления постоянномутокулег кореализую тся, ноне отличаю тсявы сокой точностью . П реиму-
щество метода измерениясопротивленияамперметром и вольтметром заклю ча-
етсявтом, чтовпроцессеизмеренияRx объ ектпоставленвусловияРабочег орежима.
Непосредственно и бы стро сопротивление может бы ть измерено с помо-
щью омметра.
3. И ЗМ Е РЕ Н И Е С О П РО ТИ В Л Е Н И Я О М М Е ТРО М
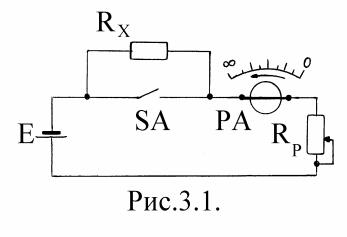
О мметры – приборы непосредственной оценки, предназначенны едляизмерениясопротивления
до нескольких |
килоом. |
П рин- |
||
ципиальны е |
схемы |
омметров |
||
приведены |
на |
рис.3.1 |
и |
рис.3.2. |
М аг нитоэлектрический |
миллиам- |
|||
перметр РА, используемы й в приборе, вклю чаю т последовательно (рис.3.1) или параллельно (рис.3.2)
резистору |
с |
неизвестны м |
сопротивлением. |
П осле подклю - |
|
ченияприбора кисточнику пита-

7
ния при замкнутом (рис.3,1) или разомкнутом (рис.3.2) контакте SA указательприбора РА припо-
мощ и переменног о резистора Rр устанавливаю т в нулевое положение. П осле переклю чения контакта SA подвижнаячастьмиллиамперметра под действием тока источника питания перемещ ается на уг ол, зависящ ий от измеряемог осопротивления.
Д ля измерения сопротивлений, превы ш аю щ их 1000 О м , применяю тпоследовательную схему(рис.3.1). П риэтом уг ол отклонения подвижной части прибора обратно пропорционаленвеличине
Rx·:
α = SI·I = SI·[E/(R+RPA +RX )],
г де SI – чувствительность прибора по току, RPA – ег о входное сопротивление. Ш калуомметра градуирую тнепосредственно вомах, поэтому у последовательной схемы омметра нулеваяотметка расположена справа.
Д ля измерения меньш их сопротивлений использую т параллельную схему омметра (рис.3.2). В этом случае уг олотклонениястрелкипропорционаленRX и нулеваяотметка ш калы таког оприбора расположена слева.
О сновны м недостатком рассмотренны х приборовявляетсязависимость показаний от напряжения источника питания. Э то требует постоянног о контроля нулевог опоказанияпередкажды м измерением.
Д ля уменьш ениявлияниянестабильности питанияна показанияприборов омметры собираю тс использованием лог ометрических измерительны х механизмов.
Д ве подвижны е катуш ки измерительног омеханизма подклю чены кобщ е- муисточнику, а резистор Rx , сопротивление которог о требуется измерить, вклю чен в цепь одной из катуш ек (рис.3.3). И змеряемое сопротивление Rx можетбы ть вклю ченопоследовательнос одной из рамок лог ометра, или парал-
лельно. Е сли токи I1 и I2 |
цепи рамок |
|
вы разить в виде: |
I1=E/(RX |
+Rp ) и I2= |
=E/(R+Rp ), г де |
Rp – сопротивление |
|
рамки лог ометра, |
то уравнение ш калы |
|
омметра можнозаписатьввиде:
α=F(I1 /I2 ) =F[(R+Rp )/(RX +Rp )]=F1(RX ).
8
Д иапазон измерений вы бираю т при помощ и резистора R. Более точное измерениесопротивлениядостиг аетсяспомощ ью схем сравнения.
4. М О С ТО В Ы Е С Х Е М Ы Д Л Я И ЗМ Е РЕ Н И Я С О П РО ТИ В Л Е Н И Я
4.1.О динарны й мост
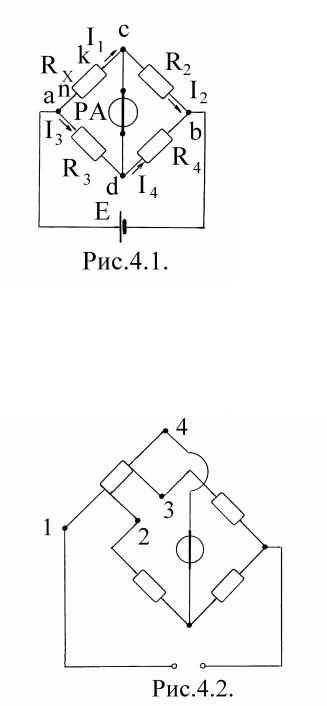
Д ляизмерениясредних сопротивлений использую тодинарны й мостпостоянног отока (рис.4.1).
В одно плечо моста вклю чаю т резистор с измеряемы м сопротивлением RX , а в три дру-
гих плеча – резисторы c известны ми рег улируемы ми сопротивлениями R2 , R3 , R4 . К диа-
гоналиab моста подклю ченисточникпитанияЕ ,
а к диаг онали cd – магнитоэлектрический
гальванометрРА.
Дляизмерениявеличины RX сопротивления R2 , R3 и R4 подбираю ттак, чтобы ток через г альванометрбы лравеннулю . В этом случае
потенциалы точекс иd одинаковы (φc= =φd ), то есть мост находится в равновесии. П ри этом
I =I ; I =I иR ·I =R ·I ; R ·I =R ·I
1 2 3 4 X 1 3 3 2 2 4 4.
Разделивпоследние два уравненияоднона друг ое, получим:
RX /R2=R3 /R4 ,
или
RX=R2·( R3 /R4).
Полученноевы ражениеназы ваетсяуравнением равновесиямоста.
Еслиизмеряемоесопротивле-
ниеRX мало, топривклю ченииег ов схемумоста на рис.4.1 возникает пог реш ность вследствие влия-
ния сопротивлений |
соединитель- |
ны х проводов an и kc, |
а такжепе- |
реходны х сопротивлений контактоввузлах плеча ас (этисопротивления имею т порядок соты х долей
ома). |
|
|
|
|
Д ля более точног о измерения |
||
малы х |
сопротивлений |
некоторы е |
|
типы |
мостов (например, М О -62 или |
||
Р |
333) |
допускаю т |
наряду с |
двухзажимны м вклю чением средних сопротивлений четы рехзажим-
9 |
|
|
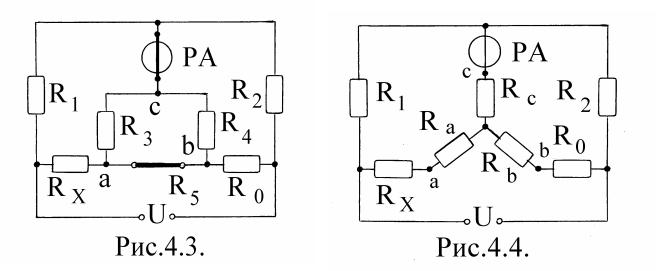
ное вклю чение резисторов с малы м сопротивлением |
(рис.4.2). |
Здесь |
цифрами 1 и 4 обозначены токовы е зажимы , а цифрами 2 и 3 – потенциальны е зажимы резистора RX. С опротивления соединительны х проводов (an и kc на рис.4.1) не влияю тна точность измерения, таккаквсхеме на рис.4.2 они вклю - чены вдиаг оналимоста.
Более точны е измерения малы х сопротивлений в лабораторны х условиях вы полняю тспомощ ью двойног омоста.
4.2. Д войной мост
Анализ работы схемы двойног омоста (рис.4.3) удобнеевы полнять, предварительнозаменивтреуг ольниксопротивлений R3 , R4 , R5 на эквивалентную звез-
ду(рис.4.4).
П реобразованная схема (рис.4.4) представляетсобой четы рехплечий мост (аналог ичны й мостуна рис.4.1). М остуравновеш енприусловии:
R1·(R0+Rb)=R2·(RX+Ra).
ЗдесьсопротивленияRa иRb определяю тсявы ражениями:
Ra=(R3·R5)/(R3+R4+R5);
Rb=(R4·R5)/(R3+R4+R5).
П одстановка этих вы ражений вуравнениеравновесиямоста дает:
R1·[R0+(R4·R5)/(R3+R4+R5)]=R2·[RX +(R3·R5)/(R3+R4+R5)];
следовательно
R1·[R0(R3+R4+R5)+ R4·R5]/ (R3+R4+R5)=R2·[RX(R3+R4+R5)+ R3·R5]/(R3+R4+R5),
R2·RX·(R3+R4+R5)= R1·R0·(R3+R4+R5)+R1·R4·R5 –R2·R3·R5;
RX= (R1·R0 )/R2 +[R5 /(R3+R4+R5)·[(R1·R4 /R2 )-(R2·R /R2 )];
окончательно:
RX= (R1·R0 )/R2 + (R4·R5 )·[(R1 /R2 ) –(R3 /R4 )]/(R3+R4+R5).
П ри вы полнении условия R1 /R2 = R3 /R4 второе слаг аемое последнег о уравненияобращ аетсявноль и измеряемое сопротивление определяетсяпо упрощ енной формуле: RX= (R1·R0 )/R2 .
|
|
10 |
|
R1 |
/R2 = R3 /R4 |
Д ля |
тог о чтобы неточность вы полнения равенства |
||||
не давала |
заметной погреш ности, |
сопротивление R5 |
соединительног о провода |
||
должно бы ть достаточно малы м, |
а сопротивления R1 |
, R2 , R3 |
, R4 |
, наоборот, |
|
должны бы ть больш ими (покрайней мере, не меньш е 10 О м ), чтопозволяетисклю чить погреш ности, обусловленны е сопротивлениями соединительны х проводовсхемы .
П ри RX=10-5… 10-6 О м пог реш ность при измерении с помощ ью |
двойног о |
моста не превы ш ает± 1%, а при измерении сопротивлений RX>10-3 О м |
пог реш - |
ностьнепревы ш ает± 0,05%. |
|
5. М О С ТО В Ы Е С Х Е М Ы Д Л Я И ЗМ Е РЕ Н И Я |
|
Е М КО С ТИ И И Н Д У КТИ В Н О С ТИ |
|
Д ля измерения индуктивности и емкости наиболее ш ироко применяю тся мосты переменног отока.
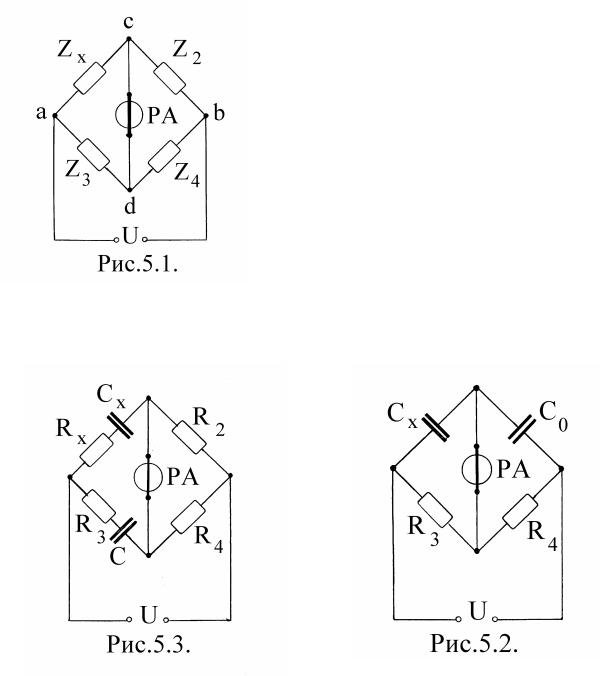
Приравновесиимоста, когда токвдиа-
гонали cd моста равен нулю , комплексны е сопротивлениявплечах моста связаны соотнош ением: Zx·Z4=Z2·Z3, следовательно,
Zx=Z2·(Z3 /Z4 ).
Д ля измерения емкости Cx конденсатора без потерь служитмостпеременног о тока, схема которог о приведена на рис.5.2. Здесь
Zx=1/i·ω ·Cx ; Z2=1/ i·ω ·C0 ; Z3=R3; Z4=R4. П од-
становка этих значений вуравнениеравновесиямоста дает: (1/Cx )=(1/C0 )·(R3 /R4); следо-
вательно, Cx=C0·(R4 /R3).
Д ляконденсаторовспотерями измерениеег оемкости, добротности Q и танг енса уг ла потерь tgδ может бы ть вы полнено по
