
2. Задания к лабораторной работе
Задание 1. Определение
коэффициента упругости пружины.
Коэффициент упругости (жёсткость)
пружины
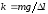 находят по её удлинению
находят по её удлинению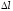 под действием груза
под действием груза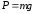 .
Для этого пружину с прикреплённой
площадкой для грузов подвешивают к
стойке, фиксируют начальное положение
нижней площадки
.
Для этого пружину с прикреплённой
площадкой для грузов подвешивают к
стойке, фиксируют начальное положение
нижней площадки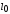 ,
затем добавляют грузы и каждый раз
записывают новое положение
,
затем добавляют грузы и каждый раз
записывают новое положение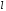 нижней части площадки по линейке. При
этом грузы не должны совершать колебания.
То же проделывают для других пружин.
Результаты измерений записывают в
таблицу 1 и по полученным данным вычисляют
средний коэффициент упругости (жёсткость)
каждой пружины,
нижней части площадки по линейке. При
этом грузы не должны совершать колебания.
То же проделывают для других пружин.
Результаты измерений записывают в
таблицу 1 и по полученным данным вычисляют
средний коэффициент упругости (жёсткость)
каждой пружины,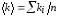 ,
где
,
где - число измерений.
- число измерений.
Таблица 1
Определение коэффициента упругости пружины
|
Пружина
1,
| ||||
|
|
m, кг |
|
|
|
|
1 2 3 4 |
|
|
|
|
|
Пружина
2,
| ||||
|
|
m, кг |
|
|
|
|
1 2 3 4 |
|
|
|
|
|
Последовательное
соединение пружин
| ||||
Подвешивают общую
массу грузов ( )
к двум пружинам, соединённым друг за
другом (последовательно). На каждую
пружину по третьему закону Ньютона
действует одна и та же сила, равная
)
к двум пружинам, соединённым друг за
другом (последовательно). На каждую
пружину по третьему закону Ньютона
действует одна и та же сила, равная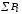 .
Общее удлинение
.
Общее удлинение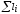 равно сумме удлинения отдельных пружин.
Общий коэффициент упругости, полученный
из опыта
равно сумме удлинения отдельных пружин.
Общий коэффициент упругости, полученный
из опыта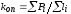 ,
сравнивают с расчётным (kp)
значением
,
сравнивают с расчётным (kp)
значением
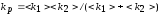 и записывают в
таблицу 1.
и записывают в
таблицу 1.
Задание 2. Определение
зависимости периода собственных
колебаний пружинного маятника от массы
груза. Для
этого подвешивают груз к одной из пружин,
коэффициент жёсткости которой известен.
Оттягивая пружину рукой, приводят её в
колебательное движение и измеряют по
секундомеру время
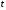 числа
числа колебаний. Период колебаний
колебаний. Период колебаний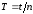 .
Затем определяют периоды колебаний с
другими грузами. Результаты вычислений
и измерений заносят в таблицу 2. Масса
площадки грузов учитывается.
.
Затем определяют периоды колебаний с
другими грузами. Результаты вычислений
и измерений заносят в таблицу 2. Масса
площадки грузов учитывается.
Таблица 2
Определение зависимости периода колебаний груза на пружине от его массы
|
Опыт |
Пружина
,
|
Теор.
( | |||||
|
|
|
|
|
|
| ||
|
1 2 3 4 |
|
|
|
|
|
| |
Теоретическое
значение периода
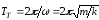 ;
;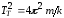 .
Сравнивают значения квадратов периодов
опытного
.
Сравнивают значения квадратов периодов
опытного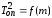 и теоретического
и теоретического .
.
Задание 3. Определение
зависимости собственных колебаний
пружинного маятника от коэффициента
упругости.
Для этого измеряют время
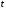 нескольких
нескольких колебаний одного и того же груза
колебаний одного и того же груза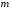 на различных пружинах. Затем определяют
значение периода опытного (
на различных пружинах. Затем определяют
значение периода опытного (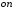 )
и теоретического (
)
и теоретического ( )
колебаний для каждой пружины по формулам
)
колебаний для каждой пружины по формулам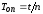 и
и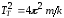 .
Масса площадки для грузов учитывается.
Результаты измерений и вычислений
заносят в таблицу 3.
.
Масса площадки для грузов учитывается.
Результаты измерений и вычислений
заносят в таблицу 3.
Таблица 3
Определение зависимости собственных колебаний пружинного маятника
от коэффициента упругости
|
Пружина |
Масса
|
Теор. ( | |||||
|
|
|
|
|
|
| ||
|
1 2 |
|
|
|
|
|
| |
Сравнивают
значения квадратов периодов опытного
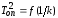 и теоретического
и теоретического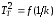 .
.
Задание 4. Определение
коэффициента упругости двух одинаковых
пружин, соединённых параллельно, по
периоду колебаний.
Для этого фиксируют в опытах время
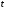 число
число колебаний для одной пружины и двух
пружин, соединённых параллельно. Затем
для одной пружины и двух пружин вычисляют
периоды
колебаний для одной пружины и двух
пружин, соединённых параллельно. Затем
для одной пружины и двух пружин вычисляют
периоды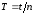 ,
среднее значение
,
среднее значение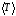 и коэффициенты упругости
и коэффициенты упругости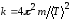 .
Результаты измерений и вычислений
заносят в таблицу 4.
.
Результаты измерений и вычислений
заносят в таблицу 4.
Таблица 4
Определение коэффициента упругости двух одинаковых пружин, соединённых параллельно, по периоду колебаний
|
Одна
пружина,
|
Две
пружины,
| |||||
|
Опыт |
|
|
|
|
|
|
|
1 2 3
|
|
|
|
|
|
|
|
|
| |||||
Коэффициент
упругости для двух пружин, соединенных
параллельно,
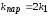 .
.
Задание 5. Определение
логарифмического декремента затухания
пружинного маятника методом сравнения
амплитуд.
Один из грузов помещают на пружину и
приводят в колебание. Измеряют время
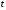 ,
за которое начальная амплитуда
,
за которое начальная амплитуда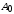 уменьшается в 10 раз, т.е.
уменьшается в 10 раз, т.е.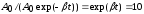 .
Откуда логарифмический декремент
затухания пружинного маятника
.
Откуда логарифмический декремент
затухания пружинного маятника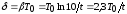 .
Значение
.
Значение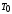 берут из таблицы 2 для той пружины, с
которой проводили данное измерение.
берут из таблицы 2 для той пружины, с
которой проводили данное измерение.
Вычисляют по
формулам коэффициент затухания
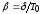 ,
коэффициент сопротивления (трения)
,
коэффициент сопротивления (трения)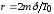 ,
добротность
,
добротность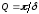 ,
время релаксации
,
время релаксации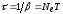 ,
число колебаний за время релаксации
,
число колебаний за время релаксации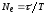 .
Значения измерений и вычислений заносят
в таблицу 5.
.
Значения измерений и вычислений заносят
в таблицу 5.
Таблица 5
Определение логарифмического декремента затухания пружинного маятника методом сравнения амплитуд
|
Опыт |
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
| ||||||
|
Средние значения |
|
|
|
|
|
| |||||||

 м
м
 ,
м
,
м ,
м
,
м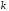 ,
Н/м
,
Н/м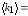 Н/м
Н/м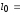 м
м
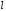 ,
м
,
м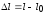 ,
м
,
м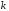 ,
Н/м
,
Н/м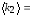 Н/м
Н/м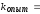 Н/м,
Н/м, Н/м
Н/м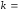 Н/м
Н/м )
)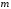 ,
кг
,
кг
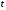 ,
с
,
с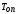 ,
с
,
с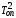 ,
с2
,
с2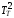 ,
с2
,
с2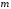 =
кг
=
кг )
)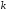 (табл.
1)
(табл.
1)
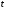 ,
с
,
с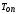 ,
с
,
с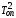 ,
с2
,
с2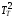 ,
с2
,
с2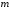 =
кг
=
кг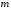 =
кг
=
кг
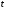 ,
с
,
с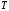 ,
с
,
с
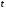 ,
с
,
с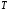 ,
с
,
с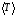 =
с
=
с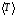 =
с
=
с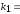 Н/м
Н/м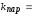 Н/м
Н/м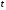 ,
с
,
с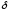
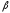 ,
с-1
,
с-1 ,
кг/с
,
кг/с
 ,
с
,
с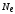
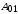 =
м
=
м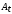 =
м
=
м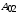 =
м
=
м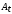 =
м
=
м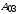 =
м
=
м =
м
=
м =
=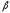 =
с-1
=
с-1 =
кг/с
=
кг/с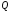 =
= =
с
=
с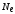 =
=