
Бельский - Теория графов и комбинаторика / Lecture13
.doc
ТЕОРИЯ ГРАФОВ И КОМБИНАТОРИКА
специальность ПО
2-й семестр
Лекция 13
Ориентированный граф и его графическая интерпретация. Локальные степени. Мат-рица смежностей. Ориентированные пути и связность в ориентированном графе.
Ориентированный
граф (или
сокращенно орграф)
- это пара множеств
![]() ,
где
,
где
![]() - любое непустое конечное множество, а
- любое непустое конечное множество, а
![]() - подмножество в
- подмножество в
 (здесь
(здесь
![]() - прямое произведение множества
- прямое произведение множества
![]() на себя, т.е. множество всех упорядоченных
пар элементов из
на себя, т.е. множество всех упорядоченных
пар элементов из
![]() ,
и
,
и
![]() - диагональ множества
- диагональ множества
![]() ).
Элементы из
).
Элементы из
![]() называются вершинами
орграфа, а элементы из
называются вершинами
орграфа, а элементы из
![]() - его ребрами.
- его ребрами.
Если
![]() и
и
![]() ,
то
,
то
![]() называется началом,
а
называется началом,
а
![]() называется концом
ребра
называется концом
ребра
![]() ;
как и в «неориентированном случае»,
вершины
;
как и в «неориентированном случае»,
вершины
![]() ,
,
![]() называются инцидентными
ребру
называются инцидентными
ребру
![]() ,
а ребро
,
а ребро
![]() называется инцидентным
вершинам
называется инцидентным
вершинам
![]() ,
,
![]() .
.
Орграф имеет
естественную геометрическую интерпретацию:
его вершины изображают-ся в виде точек
на плоскости, а ребра – в виде стрелок,
идущих из начала в конец ребра. Напри-мер,
если орграф
![]() имеет в качестве множества вершин
имеет в качестве множества вершин

![]() и в качестве множества ребер
и в качестве множества ребер

![]() ,
то геометрически он выглядит так:
,
то геометрически он выглядит так:
a2




 a1
a3
a1
a3
 a5
a4
a5
a4
Если два орграфа
![]() таковы, что одновременно выполняются
два условия -
таковы, что одновременно выполняются
два условия -
![]() и
и
![]() ,
- то говорят, что
,
- то говорят, что
![]() - подграф
орграфа
- подграф
орграфа
![]() При этом пишут:
При этом пишут:
![]() .
Если одновременно
.
Если одновременно
![]() и
и
![]() ,
то орграфы
,
то орграфы
![]() называются равными
и пишут
называются равными
и пишут
![]() .
.
Два орграфа -
![]() - называются изоморфными,
если существует отображение
- называются изоморфными,
если существует отображение
![]() такое, что выполнены следующие четыре
условия:
такое, что выполнены следующие четыре
условия:
-
если
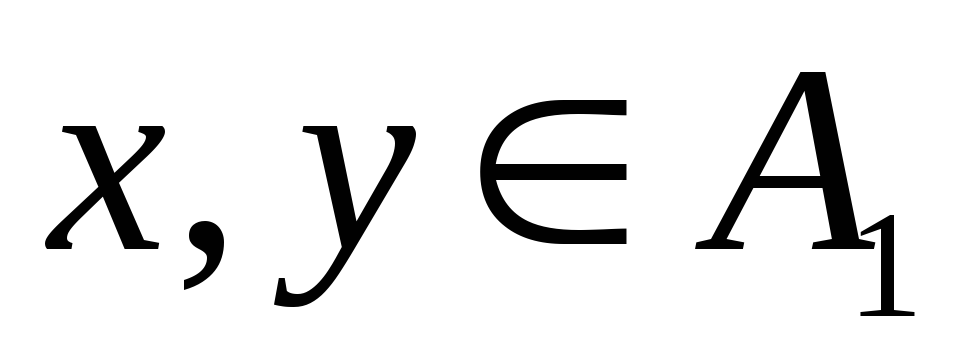 и
и
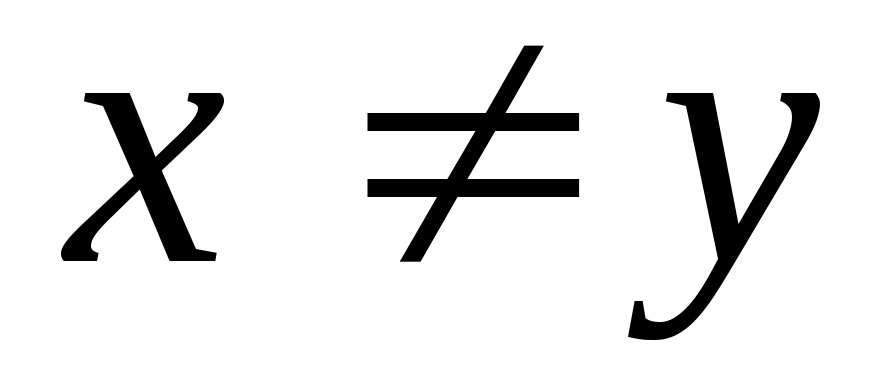 ,
то
,
то
 ;
; -
для всякого
 существует такой
существует такой
 ,
что
,
что
 ;
; -
если
 ,
то
,
то
 ;
; -
если
 и
и
 ,
то
,
то
 .
.
Если
![]() - орграф и
- орграф и
![]() ,
то следующие три числа имеют специальные
названия: число
,
то следующие три числа имеют специальные
названия: число
![]() (количество ребер, исходящих из вершины
(количество ребер, исходящих из вершины
![]() )
называется исходящей
степенью
вершины
)
называется исходящей
степенью
вершины
![]() ;
число
;
число
![]() (количество ребер, входящих в вершину
(количество ребер, входящих в вершину
![]() )
называется входящей
степенью вершины
)
называется входящей
степенью вершины
![]() ;
число
;
число
![]() называется степенью
вершины
называется степенью
вершины
![]() .
.
Каждый орграф
![]() можно описать матрицей
смежностей по
следующей схеме: если
можно описать матрицей
смежностей по
следующей схеме: если
![]() ,
то построим матрицу
,
то построим матрицу
![]()
![]() положив
положив

С каждым орграфом
![]() однозначно связывается обычный граф
однозначно связывается обычный граф
![]() ,
в котором множество вершин - то же самое
(т.е. множество
,
в котором множество вершин - то же самое
(т.е. множество
![]() ),
а множество ребер
),
а множество ребер
![]() получается «стиранием стрелок» у ребер
из множества
получается «стиранием стрелок» у ребер
из множества
![]() (т.е. если
(т.е. если
![]() ,
то
,
то
![]() тогда и только
тогда и только
тогда, когда либо
![]() ,
либо
,
либо
![]() ).
Граф
).
Граф
![]() называется ассоциированным
с орграфом
называется ассоциированным
с орграфом
![]() .
.
В каждом орграфе
![]() выделяется основной объект –
ориентированный
путь (или
кратко - орпуть)
орпуть
- это символ
выделяется основной объект –
ориентированный
путь (или
кратко - орпуть)
орпуть
- это символ
![]() ,
,
в котором
![]() (причем, в списке
(причем, в списке
![]() могут быть повторяющиеся вершины) и в
котором
могут быть повторяющиеся вершины) и в
котором
![]() .
Ясно, что при переходе от ориентированного
графа к ас-социированному с ним графу
орпуть создает конкретный обычный путь.
В приведенных только что обозначениях
вершина
.
Ясно, что при переходе от ориентированного
графа к ас-социированному с ним графу
орпуть создает конкретный обычный путь.
В приведенных только что обозначениях
вершина
![]() называется началом
орпути, а
вершина
называется началом
орпути, а
вершина
![]() называется концом
орпути. При этом о самом орпути говорят,
что он является
орпутем из
называется концом
орпути. При этом о самом орпути говорят,
что он является
орпутем из
![]() в
в
![]() .
.
Две вершины
![]() орграфа называются связанными,
если имеется орпуть из
орграфа называются связанными,
если имеется орпуть из
![]() в
в
![]() и одновременно имеется орпуть из
и одновременно имеется орпуть из
![]() в
в
![]() .
Орграф называется связным,
если в нем любые две вершины связанны.
Так же, как в неориентированном случае,
понятие связности приводит к понятию
связной компоненты: подграф
.
Орграф называется связным,
если в нем любые две вершины связанны.
Так же, как в неориентированном случае,
понятие связности приводит к понятию
связной компоненты: подграф
![]() орграфа
орграфа
![]() называется связной
компонентой
оргра-фа
называется связной
компонентой
оргра-фа
![]() ,
если: 1)
,
если: 1)
![]() является связным орграфом; 2) не существует
связного орграфа
является связным орграфом; 2) не существует
связного орграфа
![]() такого, что
такого, что
![]() и
и
![]() .
.
Подобно тому, как это делалось в случае обычных графов, для ориентированных графов вводятся понятия цепи, простой цепи, цикла и простого цикла. Эти объекты можно исследовать по тому же плану, что и в неориентированном случае.
Бельский Аркадий Александрович. Теория графов и комбинаторика. Лекция 13
