
- •Теория автоматического управления и регулирования
- •2005 Введение
- •1. Общие сведения о системах автоматического регулирования
- •1.1. Основные задачи
- •1.2. Понятие об автоматическом регулировании
- •1.3. Разомкнутые и замкнутые системы автоматического регулирования
- •1.4. Системы автоматической стабилизации
- •1.5. Следящие системы
- •1.6. Понятие о непрерывных и прерывистых системах
- •Контрольные вопросы
- •2. Линейные и нелинейные системы автоматического регулирования. Общий метод линеаризации
- •2.1. Общие положения
- •2.2. Общий метод линеаризации
- •Контрольные вопросы
- •3. Динамические звенья и их характеристики
- •3.1. Общие положения
- •3.2. Временные характеристики звеньев
- •3.3. Частотные характеристики звеньев
- •3.4. Логарифмические частотные характеристики звеньев
- •3.5. Безынерционное звено
- •3.6. Апериодическое звено первого порядка
- •3.7. Апериодическое звено второго порядка
- •3.8. Идеальное интегрирующее звено
- •3.9. Инерционное интегрирующее звено
- •3.10. Идеальное дифференцирующее звено
- •3.11. Реальное дифференцирующее звено
- •3.12. Неустойчивые звенья
- •Контрольные вопросы
- •4. Составление и анализ исходных дифференциальных уравнений Систем Автоматического регулирования
- •4.1. Общий метод составления исходных уравнений
- •4.2. Передаточные функции систем автоматического регулирования
- •4.3. Составление уравнений на основе типовых звеньев
- •Контрольные вопросы
- •5. Устойчивость линейных систем автоматического регулирования
- •5.1. Понятие об устойчивости линейных систем
- •5.2. Алгебраический критерий устойчивости
- •1. Уравнение первого порядка
- •2. Уравнение второго порядка
- •3. Уравнение третьего порядка
- •4. Уравнение четвертого порядка
- •5.3. Критерий устойчивости Михайлова
- •5.4. Определение устойчивости по логарифмическим характеристикам
- •Контрольные вопросы
- •6. Построение кривой переходного процесса в системе автоматического регулирования
- •6.1. Общие положения
- •6.2. Классический метод
- •6.3. Метод трапецеидальных вещественных характеристик
- •Контрольные вопросы
- •7. Оценка качества регулирования
- •7.1. Общие положения
- •7.2. Точность в типовых режимах
- •7.3. Определение показателей качества регулирования по переходной характеристике
- •7.4. Приближенная оценка вида переходного процесса по вещественной частотной характеристике
- •7.5. Корневые методы
- •7.6. Частотные критерии качества
- •Контрольные вопросы
- •8. Элементы синтеза систем автоматического регулирования
- •8.1. Общие положения
- •8.2. Метод логарифмических амплитудных характеристик
- •8.3. Синтез последовательного корректирующего устройства
- •Контрольные вопросы
- •9. Нелинейные Системы автоматического регулирования
- •9.1. Методы исследования процессов в нелинейных системах
- •9.2. Метод фазовой плоскости
- •Контрольные вопросы
- •Заключение
- •Рекомендуемый Библиографический список
3.7. Апериодическое звено второго порядка
Звено относится к группе позиционных звеньев и описывается уравнением
![]() . (3.39)
. (3.39)
При этом корни характеристического уравнения
![]() (3.40)
(3.40)
должны быть вещественными, что будет выполняться при условии Т1≥ 2 Т2.
Левая часть уравнения (3.39) разлагается на множители
![]() , (3.41)
, (3.41)
где
![]() . (3.42)
. (3.42)
Передаточная функция звена
![]() . (3.43)
. (3.43)
Из последнего выражения видно, что апериодическое звено второго порядка эквивалентно двум апериодическим звеньям первого порядка, включенным последовательно друг за другом, с общим коэффициентом передачи k и постоянными времени Т3и Т4.
Примеры апериодических звеньев второго порядка приведены на рис. 3.15. Рассмотрим подробно случай двигателя постоянного тока (рис. 3.15, в). При отсутствии момента нагрузки на валу и при учете переходных процессов в цепи якоря динамика двигателя описывается двумя уравнениями, соответствующими закону равновесия эдс в цепи якоря
![]() (3.44)
(3.44)
и закону равновесия моментов на валу двигателя
![]() ,
(3.45)
,
(3.45)
где СЕи СМ – коэффициенты пропорциональности между противо эдс и скоростью вращения и между вращающим моментом и током якоря; J – приведенный момент инерции;Lи R – индуктивность и сопротивление цепи якоря.

Рис. 3.15. Апериодические звенья второго порядка
Решая уравнения (3.44) и (3.45) совместно, получим передаточную функцию двигателя постоянного тока при управлении напряжением якоря
 ,
(3.46)
,
(3.46)
где электромеханическая постоянная времени
![]() (3.47)
(3.47)
и электромагнитная постоянная времени якорной цепи
![]() .
(3.48)
.
(3.48)
Для того чтобы корни знаменателя в
(3.46) были вещественными и передаточную
функцию можно было представить в виде
(3.43) , необходимо выполнение условия
![]() .
.
Переходная функция получается путем
решения дифференциального уравнения
(3.39) при x1= 1(t)
и нулевых начальных условиях, то есть
приt= 0;x2= 0
и![]()
 .
(3.49)
.
(3.49)
Функция веса
 .
(3.50)
.
(3.50)
Временные характеристики звена изображены
на рис. 3.16 (для определенности принято
![]() ).
).
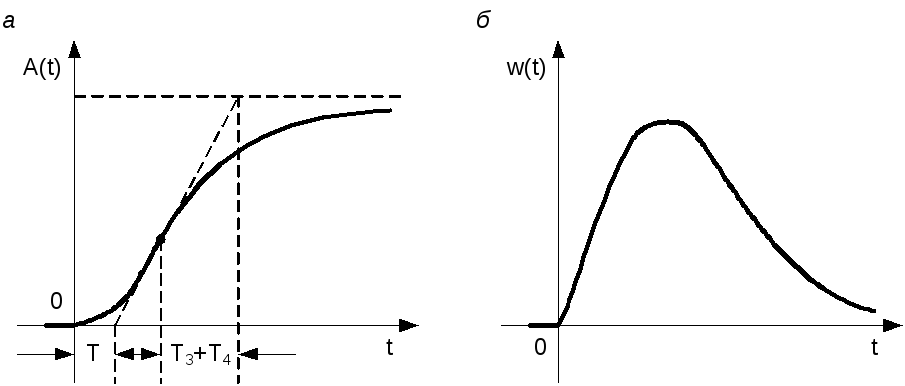
Рис. 3.16. Переходная функция (а) и дельта-функция (б) апериодического звена второго порядка
На переходной характеристике показано построение, позволяющее по экспериментальным данным определять постоянные времени Т3и Т4.
Частотная передаточная функция согласно (3.43), её модуль и фаза соответственно равны
![]() ; (3.51)
; (3.51)
 . (3.52)
. (3.52)
Амплитудная, фазовая и амплитудно-фазовая
характеристики показаны на рис. 3.17. На
амплитудно-фазовой характеристике
отмечены три характерные точки: ω= 0;![]() .
.
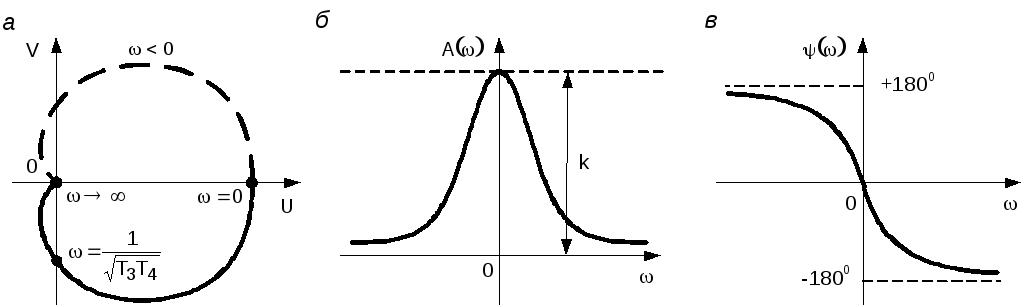
Рис. 3.17. АФЧХ (а), АЧХ (б) и ФЧХ (в) апериодического звена второго порядка
Построим теперь логарифмические характеристики (рис. 3.18). Для этой цели проведем вертикальные пунктирные прямые при сопрягающих частотах 3= 1 /T3и4= 1 /T4. Будем считать, чтоT3>T4и3<4.
ЛАХ определяется выражением
![]() . .(3.53)
. .(3.53)
Для частот, меньших, чем сопрягающая
частота ω3(а значит и меньших, чем частота ω4),
будет справедливым![]() и
и![]() .
Поэтому в этой области можно допуститьL() 20 lgk.
Этому выражению соответствует прямая
а–bна рис. 3.18.
.
Поэтому в этой области можно допуститьL() 20 lgk.
Этому выражению соответствует прямая
а–bна рис. 3.18.
Для частот ω3<
ω< ω4будет справедливым![]() и
и![]() .
Поэтому в этой области можно принятьL() 20 lg(k / T3),
чему соответствует прямая с отрицательным
наклоном 20 дБ/дек (прямаяb-с
на рис. 3.18) (подразд. 3.4, п. 2).
.
Поэтому в этой области можно принятьL() 20 lg(k / T3),
чему соответствует прямая с отрицательным
наклоном 20 дБ/дек (прямаяb-с
на рис. 3.18) (подразд. 3.4, п. 2).
Для частот
![]() имеем соответственно
имеем соответственно![]() и
и![]() ,
а такжеL() 20 lg(k / T3T4),
чему соответствует прямая с отрицательным
наклоном 40 дБ/дек (прямая с–d на рис.
3.18) (см. подразд. 3.4, п. 3).
,
а такжеL() 20 lg(k / T3T4),
чему соответствует прямая с отрицательным
наклоном 40 дБ/дек (прямая с–d на рис.
3.18) (см. подразд. 3.4, п. 3).
Ломаная линия а–b–с–d представляет собой асимптотическую ЛАХ. Действительная ЛАХ показана пунктиром. Она будет расходиться с асимптотической ЛАХ в местах изломов на 3 дБ.

Рис. 3.18. ЛАХ и ЛФХ апериодического звена второго порядка
ЛФХ получается суммированием двух
слагаемых (см. второе уравнение (3.52)).
Каждое слагаемое дает фазовую
характеристику, совпадающую с ЛФХ
апериодического звена первого порядка
(рис. 3.18). В результате суммирования
получаем ЛФХ, ордината которой
соответствует
![]() при
при![]() и
и![]() .
.
