Линейные обыкновенные дифференциальные уравнения и системы

     Линейное однородное уравнение первого порядка

     Общее решение: .

     Решение задачи Коши, y(x₀) = y₀:

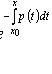
     Линейное неоднородное уравнение первого порядка

     Общее решение:

     Решение задачи Коши, y(x₀) = y₀:

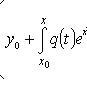
     Линейное однородное уравнение второго порядка с постоянными коэффициентами

     Характеристическое уравнение

     Характеристические числа

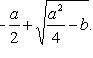
 Общее решение

     1. В случае

     Если то общее решение можно записать и в форме

     2. В случае

     Линейное неоднородное уравнение второго порядка с постоянными коэффициентами

     Общее решение неоднородного уравнения есть сумма общего решения однородного уравнения и некоторого частного решениянеоднородного.

     Вид частного решения неоднородного уравнения в некоторых конкретных случаях

     1. - многочлен степениm:

     а) число 0 не является корнем характеристического уравнения , т. е., тогда

где - многочлен порядкаm;

     б) число 0 - корень характеристического уравнения, т. е. b = 0, тогда

если 0 - простой корень, т. е. ;

если 0 - кратный корень, т. е. a = 0.

   2. :

     а) число не является корнем характеристического уравнения, тогда

     б) - корень характеристического уравнения:

если - простой корень;

если - кратный корень.

     3. :

     а) число не является корнем характеристического уравнения, тогда

     б) корень характеристического уравнения:

     4. :

     а) число не является корнем характеристического уравнения, тогда

     б) - корень характеристического уравнения:

Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами

     Характеристическое уравнение

- корни характеристического уравнения.

     Общее решение

     1. Все корни характеристического уравнения различные, тогда

     Если среди корней есть пары комплексно-сопряженных корней, например , решение можно записать в виде

     2. Среди корней характеристического уравнения есть кратные, например, имеет кратностьk (остальные - простые), тогда

     Если среди корней есть пары сопряженных корней кратности k, например , решение можно записать в виде

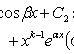
Линейное неоднородное уравнение с постоянными коэффициентами

     Общее решение неоднородного уравнения есть сумма общего решения однородного уравнения и некоторого частного решения неоднородного уравнения.

  Вид частного решения y* неоднородного уравнения в некоторых конкретных случаях

(- заданные многочлены степениm, l; - искомые многочлены степени не вышеm, k)

     1. :

     a) число 0 не является корнем характеристического уравнения, тогда

     б) число 0 - корень кратности s характеристического уравнения:

     2. :

     a) число a не является корнем характеристического уравнения, тогда

     б) число a - корень кратности s характеристического уравнения:

     3. :

     a) числа не являются корнями характеристического уравнения, тогда

     б) числа - корни кратностиs:

     4. :

     a) числа не являются корнями характеристического уравнения, тогда

     б) числа - корни кратностиs:

Принцип суперпозиции

     Если y_k(x) - решение линейного уравнения

     то - решение уравнения

     Метод Лагранжа вариации произвольных постоянных при нахождении общего решения линейного неоднородного уравнения

     Если известно общее решение

(C₁, C₂, ..., C_n - произвольные постоянные) однородного уравнения

то общее решение неоднородного уравнения

можно искать в виде

     определяются из системы

     Уравнение Эйлера

(a_n-1, a_n-2, ..., a₀ - постоянные) заменой независимой переменной x = e^t сводится к линейному уравнению с постоянными коэффициентами вида

Линейная однородная система дифференциальных уравнений с постоянными коэффициентами

     В векторной форме:

dY/dx = AY,

где

     Характеристическое уравнение

или .

     Нахождение общего решения системы по методу Эйлера

     1. Если - простой корень характеристического уравнения, то ему соответствует решение

числа находятся из системы

  2. Если - корень кратностиm характеристического уравнения, то ему соответствует решение вида

где P₁(x), P₂(x), ..., P_n(x) - многочлены степени не выше m-1, имеющие в совокупности m произвольных постоянных.

     Коэффициенты многочленов можно определить, подставив выражения для y₁, y₂, ..., y_n в исходную систему.

     Найдя решения, соответствующие каждому корню характеристического уравнения, общее решение системы получим как линейную комбинацию этих решений.

     Например, если все корни характеристического уравнения простые, а решениями, соответствующими этим корням , будут:

то общее решение этой системы имеет вид:
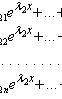