2 Автомати з пам’яттю
Автомати з пам’яттю (АП) – це такі дискретні пристрої, які крім логічних елементів мають елементи пам’яті. Вони забезпечують зберігання інформації, чого не могли комбінаційні схеми. Для зберігання інформації використовуються спеціальні елементи пам’яті, які зберігають один біт інформації. Ці елементи називаються тригерами – прості автомати з пам’яттю, які мають два внутрішні стани: нуль та одиниця.
Дискретні АП характеризуються тим, що стан їх виходів залежить як від сигналів, які присутні на їх входах в даний момент часу, так і від послідовності сигналів, які надійшли на входи автомата в попередні моменти часу. АП називають багатотактними автоматами. Кажуть, що вони функціонують в дискретному часі. Це означає, що АП здійснюють перетворення інформації в окремі дискретні моменти часу. Дискретні моменти часу можуть задаватися або зовнішніми подіями (асинхронний АП), або від спеціального генератора, який синхронізує імпульси (синхронний АП).
В загальному випадку функціонування автомату з пам’яттю зводиться до зміни його внутрішнього стану під дією вхідних сигналів. Код внутрішнього стану АП утворюється сукупністю сигналів внутрішнього стану елементів пам’яті. Зміна кодів описується функцією переходів, при цьому формуються певні вихідні сигнали (позначаються z), які описуються функцією виходу. Усі АП починають функціонування з певного стану, який називається початковим і позначається S0.
Синтез АП складається з наступних етапів:
1) словесне описання алгоритму роботи АП;
2) складання графів переходів-виходів;
3) побудова таблиці переходів-виходів;
4) мінімізація кількості станів;
5) визначення кількості тригерів та складання функціональної таблиці;
6)
складання функцій, які задають сигнали
на входах тригерів та вихідного сигналу;
7) побудова схеми автомата.
2.1 АП 1
АП 1 - послідовностний автомат на 2 входи і один вихід. Вхідна інформація: трьохрозрядні числа n1, n2, які надходять послідовно, починаючи зі старшого значущого розряду. Вихідна інформація: послідовне представлення Z=max (n1,n2).
Рисунок 2.1 – Загальний вигляд АП 1
Спочатку складається графів переходів-виходів для АП 1 (рисунок 2.2):
Рисунок 2.2 Граф переходів-виходів АП 1
Далі
складається таблиця переходів-виходів
(таблиця 2.1):
Таблиця 2.1 - Таблиця переходів-виходів АП 1
-
S(t)
n1n2(t)
00
01
10
11
S0
S1,0
S4,1
S3,1
S2,1
S1
S5,0
S8,1
S7,1
S6,1
S2
S9,0
S12,1
S11,1
S10,1
S3
S13,0
S16,0
S15,1
S14,1
S4
S17,0
S20,1
S19,0
S18,1
S5
S0,0
S0,1
S0,1
S0,1
S6
S0,0
S0,1
S0,1
S0,1
S7
S0,0
S0,0
S0,1
S0,1
S8
S0,0
S0,1
S0,0
S0,1
S9
S0,0
S0,1
S0,1
S0,1
S10
S0,0
S0,1
S0,1
S0,1
S11
S0,0
S0,0
S0,1
S0,1
S12
S0,0
S0,1
S0,0
S0,1
S13
S0,0
S0,0
S0,1
S0,1
S14
S0,0
S0,0
S0,1
S0,1
S15
S0,0
S0,0
S0,1
S0,1
S16
S0,0
S0,0
S0,1
S0,1
S17
S0,0
S0,1
S0,0
S0,1
S18
S0,0
S0,1
S0,0
S0,1
S19
S0,0
S0,1
S0,0
S0,1
S20
S0,0
S0,1
S0,0
S0,1
S21
S0,0
S0,0
S0,0
S0,0
Після мінімізації кількості станів (об’єднання строк в таблиці переходів-виходів, якщо значення станів і виходів, вказаних у відповідних клітинках кожної із порівнюваних строк співпадають) таблиця 2.1 перетворюється в таблицю 2.2:
Таблиця 2.2 - Таблиця переходів-виходів АП 1
-
S(t)
n1n2(t)
00
01
10
11
1
2
3
4
5
S0
S1,0
S4,1
S3,1
S2,1
S1
S5,6,9,10,0
S8,12,17-20,1
S7,11,13-16,1
S5,6,9,10,1
S2
S5,6,9,10,0
S8,12,17-20,1
S7,11,13-16,1
S5,6,9,10,1
Продовження таблиці 2.2
-
1
2
3
4
5
S3
S7,11,13-16,0
S7,11,13-16,0
S7,11,13-16,1
S7,11,13-16,1
S4
S8,12,17-20,0
S8,12,17-20,1
S8,12,17-20,0
S8,12,17-20,1
S5,6,9,10
S0,0
S0,1
S0,1
S0,1
S7,11,13-16
S0,0
S0,0
S0,1
S0,1
S8,12,17-20
S0,0
S0,1
S0,0
S0,1
S21
S0,0
S0,0
S0,0
S0,0
Таблиця 2.3 - Таблиця переходів-виходів АП 1
-
S(t)
n1n2(t)
Код
стану
00
01
10
11
S0
S1,2,0
S4,1
S3,1
S1,2,1
000
S1,2
S5,6,9,10,0
S8,12,17-20,1
S7,11,13-16,1
S5,6,9,10,1
001
S3
S7,11,13-16,0
S7,11,13-16,0
S7,11,13-16,1
S7,11,13-16,1
010
S4
S8,12,17-20,0
S8,12,17-20,1
S8,12,17-20,0
S8,12,17-20,1
011
S5,6,9,10
S0,0
S0,1
S0,1
S0,1
100
S7,11,13-16
S0,0
S0,0
S0,1
S0,1
101
S8,12,17-20
S0,0
S0,1
S0,0
S0,1
110
S21
S0,0
S0,0
S0,0
S0,0
111
На наступному етапі, приймаючи
до уваги кількість станів автомату,
визначається кількість тригерів, які
забезпечують реалізацію цих станів та
їх тип. В даному випадку використано
три тригери
(відповідно
до завдання).
Далі складається функціональна
таблиця
(таблиця 2.4):
Таблиця 2.4 - Функціональна таблиця АП 1
-
t
t+1
T1
T2
T3
z
n1
n2
y1
y2
y3
y1
y2
y3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0
0
0
0
0
0
0
1
1
~
1
~
0
1
0
0
0
0
0
1
1
0
0
0
1
1
~
1
0
0
0
0
0
1
0
1
0
1
0
1
1
0
0
1
0
0
0
0
1
1
1
1
0
0
1
~
1
1
0
0
0
0
1
0
0
0
0
0
1
0
1
~
1
~
0
0
0
1
0
1
0
0
0
1
0
1
~
1
0
0
0
0
1
1
0
0
0
0
1
0
1
0
1
~
0
0
0
1
1
1
0
0
0
1
0
1
0
1
0
0
Продовження
таблиці 2.4
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0
1
0
0
0
0
1
1
1
~
0
1
0
1
1
0
1
0
0
1
1
1
0
0
1
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0
0
1
0
0
1
0
1
1
1
1
0
0
1
~
1
1
0
1
0
1
1
0
0
0
0
0
1
0
1
~
1
~
1
0
1
1
0
1
0
0
0
1
0
1
~
1
0
0
0
1
1
1
0
0
0
0
1
0
1
0
1
~
1
0
1
1
1
1
0
0
0
1
0
1
0
1
0
0
1
0
0
0
0
0
1
0
1
~
0
1
1
~
1
1
0
0
0
1
1
0
1
0
1
1
~
~
1
1
1
0
0
1
0
1
0
1
0
1
1
0
0
1
1
1
0
0
1
1
1
1
0
0
1
~
1
1
0
0
1
0
1
0
0
0
0
0
1
0
1
~
1
~
1
1
0
1
0
1
0
0
0
1
0
1
~
1
0
1
1
0
1
1
0
0
0
0
1
0
1
0
1
~
0
1
0
1
1
1
0
0
0
1
0
1
0
1
0
0
1
1
0
0
0
0
0
1
1
~
1
~
0
1
1
1
1
0
0
1
1
0
0
0
1
1
~
1
0
1
1
1
0
1
0
1
0
1
0
1
1
0
0
1
1
1
1
0
1
1
1
1
0
0
1
~
1
1
0
1
1
1
1
0
0
0
0
0
1
0
1
~
1
~
1
1
1
1
0
1
0
0
0
1
0
1
~
1
0
1
1
1
1
1
0
0
0
0
1
0
1
0
1
~
1
1
1
1
1
1
0
0
0
1
0
1
0
1
0
0
Далі складаються функції, які задають сигнали на входах тригерів та вихідного сигналу. Для цього складаються відповідні карти Карно і проводиться мінімізація функцій.
Рисунок 2.3 – Карта Карно для
функції виходу z
Рисунок 2.4
– Карти Карно для входів
,
,
,
,
Рисунок 2.5 – Карта Карно для
входу
Після утворення функцій реалізується схема автомата (рисунок 2.6).
2.2 АП
2 – чотирьохзозрядний реверсивний
лічильник в коді Грея
Лічильник імпульсів – автомат з пам’яттю призначений для підрахунку імпульсів. Кожний підрахований імпульс відповідає певному коду внутрішнього стану.
Лічильники поділяються на:
- лічильники прямого підрахунку;
- лічильники зворотнього підрахунку;
- комбіновані (реверсивні) лічильники.
Також розрізняють такі лічильники:
- лічильники за модулем (модуль підрахунку визначає кількість робочих станів);
- двійково-десятичний лічильник;
- лічильник в коді Грея.
Код Грея (циклічний) – характерний тим, що кожна його наступна комбінація відрізняється від попередньої в одному розряді. Перша та остання комбінації коду також відрізняються лише одним розрядом.
Для
побудови лічильника спочатку слід
закодувати його робочі стани (рисунок
2.7).
Рисунок 2.7 – а) робочі стани закодовані для прямого підрахунку;б) робочі стани закодовані для зворотнього підрахунку
Далі будується функціональна таблиця АП 2 (таблиця 2.5), де сигнал А0 визначає в прямому чи зворотньому порядку буде рахувати лічильник.
Таблиця 2.5 – Функціональна таблиця АП 2
|
t |
t+1 |
Тригери |
||||||||||||||
|
А0 |
у1 |
у2 |
у3 |
у4 |
у1 |
у2 |
у3 |
у4 |
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
~ |
0 |
1 |
|
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
~ |
1 |
~ |
0 |
1 |
~ |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
~ |
0 |
1 |
~ |
1 |
1 |
~ |
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
~ |
1 |
~ |
~ |
1 |
1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
~ |
1 |
1 |
~ |
1 |
~ |
|
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
~ |
~ |
1 |
1 |
~ |
1 |
0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
~ |
~ |
1 |
~ |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
~ |
~ |
1 |
1 |
0 |
~ |
1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
~ |
1 |
~ |
1 |
~ |
|
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
~ |
1 |
1 |
~ |
1 |
~ |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
~ |
1 |
1 |
~ |
~ |
1 |
0 |
1 |
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
~ |
1 |
1 |
~ |
1 |
0 |
~ |
1 |
|
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
1 |
1 |
~ |
0 |
1 |
|
0 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
~ |
1 |
~ |
1 |
0 |
1 |
~ |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
~ |
1 |
1 |
0 |
~ |
1 |
1 |
~ |
Продовження
таблиці 2.5
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
~ |
1 |
~ |
1 |
~ |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
~ |
|
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
0 |
|
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
~ |
1 |
~ |
~ |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
1 |
0 |
~ |
1 |
|
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
~ |
~ |
1 |
1 |
~ |
0 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
~ |
~ |
1 |
0 |
1 |
~ |
1 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
~ |
1 |
0 |
~ |
1 |
1 |
~ |
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
~ |
~ |
1 |
~ |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
~ |
1 |
1 |
~ |
1 |
~ |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
~ |
1 |
1 |
~ |
0 |
1 |
~ |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
~ |
1 |
0 |
1 |
~ |
1 |
1 |
~ |
|
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
~ |
1 |
1 |
~ |
~ |
1 |
1 |
0 |
|
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
~ |
1 |
1 |
~ |
1 |
~ |
|
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
~ |
1 |
~ |
1 |
1 |
~ |
1 |
0 |
|
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
1 |
1 |
0 |
~ |
1 |
Після складання функціональної таблиці будуються карти Карно для мінімізації функцій входів тригерів (рисунки 2.8, 2.9) та утворюються відповідні вирази функцій.
Рисунок 2.8 – Карти Карно для
входів
Рисунок
2.9 – Карти Карно для входів
Після
утворення виразів синтезується схема
АП 2 (додаток Б).
2.3 АП 3
АП 3 - послідовностний автомат на 2 входи і один вихід. Вхідна інформація: трьохрозрядні числа n1, n2, які надходять послідовно, починаючи зі старшого значущого розряду. Вихідна інформація: послідовне представлення Z=min (n1,n2).
Рисунок 2.10 – Загальний вигляд АП 3
Для синтезування АП 3 виконуються дії аналогічно тим, які виконувались для побудови АП 1 (див. підрозділ 2.1).
Рисунок 2.11 – Граф переходів-виходів
АП 3
Таблиця 2.6 - Таблиця переходів-виходів АП 3
-
S(t)
n1n2(t)
00
01
10
11
1
2
3
4
5
S0
S1,0
S4,0
S3,0
S2,1
S1
S5,0
S8,0
S7,0
S6,1
S2
S9,0
S12,0
S11,0
S10,1
S3
S13,0
S16,1
S15,0
S14,1
S4
S17,0
S20,0
S19,1
S18,1
S5
S0,0
S0,0
S0,0
S0,1
S6
S0,0
S0,0
S0,0
S0,1
S7
S0,0
S0,1
S0,0
S0,1
S8
S0,0
S0,0
S0,1
S0,1
S9
S0,0
S0,0
S0,0
S0,1
S10
S0,0
S0,0
S0,1
S0,1
S11
S0,0
S0,1
S0,1
S0,1
S12
S0,0
S0,0
S0,1
S0,1
S13
S0,0
S0,1
S0,0
S0,1
S14
S0,0
S0,1
S0,0
S0,1
S15
S0,0
S0,1
S0,0
S0,1
S16
S0,0
S0,1
S0,0
S0,1
S17
S0,0
S0,0
S0,1
S0,1
S18
S0,0
S0,0
S0,0
S0,1
S19
S0,0
S0,0
S0,1
S0,1
S20
S0,0
S0,0
S0,1
S0,1
Таблиця 2.7 - Таблиця переходів-виходів АП 3
-
S(t)
n1n2(t)
Код
стану
00
01
10
11
S0
S1 ,0
S4,0
S3,0
S2,1
000
S1
S5,6,9,10,0
S7,11,13-16,0
S8,12,17-20,0
S5,6,9,10,1
001
S2
S5,6,9,10,0
S8,12,17-20,0
S7,11,13-16,0
S5,6,9,10,1
010
S3
S7,11,13-16,0
S7,11,13-16,0
S7,11,13-16,1
S7,11,13-16,1
011
S4
S8,12,17-20,0
S8,12,17-20,0
S8,12,17-20,1
S8,12,17-20,1
100
S5,6,9,10
S0,0
S0,0
S0,0
S0,1
101
S7,11,13-16
S0,0
S0,1
S0,0
S0,1
110
S8,12,17-20
S0,0
S0,0
S0,1
S0,1
111
Таблиця
2.8 - Функціональна таблиця АП 3
-
t
t+1
T1
T2
T3
z
n1
n2
y1
y2
y3
y1
y2
y3
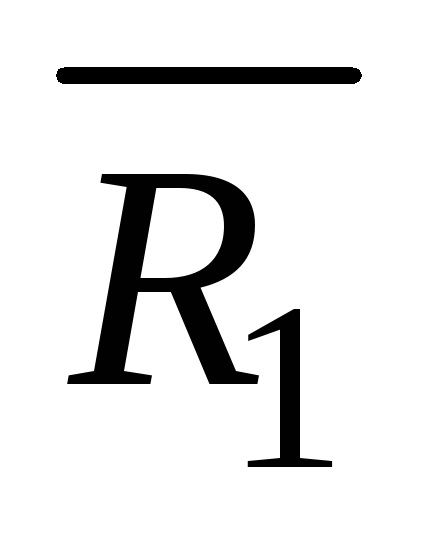
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0
0
0
0
0
0
0
1
1
~
1
~
0
1
0
0
0
0
0
1
1
0
0
0
1
1
~
1
0
0
0
0
0
1
0
0
1
1
1
~
~
1
0
1
0
0
0
0
1
1
0
1
0
1
~
~
1
1
0
0
0
0
1
0
0
0
0
0
1
0
1
~
1
~
0
0
0
1
0
1
0
0
0
1
0
1
~
1
0
0
0
0
1
1
0
0
0
0
1
0
1
0
1
~
0
0
0
1
1
1
0
0
0
1
0
1
0
1
0
0
0
1
0
0
0
1
0
1
0
1
1
~
0
1
0
0
1
0
0
1
1
0
0
0
1
1
~
1
0
0
0
1
0
1
0
1
1
1
0
1
~
1
0
1
0
0
1
0
1
1
1
1
0
0
1
~
1
1
0
0
0
1
1
0
0
0
0
0
1
0
1
~
1
~
0
0
1
1
0
1
0
0
0
1
0
1
~
1
0
0
0
1
1
1
0
0
0
0
1
0
1
0
1
~
1
0
1
1
1
1
0
0
0
1
0
1
0
1
0
0
1
0
0
0
0
1
1
0
0
1
0
1
1
~
0
1
0
0
0
1
1
1
1
0
1
0
1
~
1
0
1
0
0
1
0
0
1
1
1
~
~
1
0
1
0
1
0
0
1
1
0
0
1
1
~
1
0
~
1
1
1
0
1
0
0
0
0
0
1
0
1
~
1
~
1
1
0
1
0
1
0
0
0
1
0
1
~
1
0
0
1
0
1
1
0
0
0
0
1
0
1
0
1
~
0
1
0
1
1
1
0
0
0
1
0
1
0
1
0
1
1
1
0
0
0
0
0
1
1
~
1
~
0
1
1
1
1
0
0
1
1
0
1
0
1
1
~
~
1
1
1
1
0
1
0
1
1
1
0
1
~
1
0
1
1
1
1
0
1
1
0
1
1
1
~
~
1
~
1
1
1
1
1
0
0
0
0
0
1
0
1
~
1
~
1
1
1
1
0
1
0
0
0
1
0
1
~
1
0
1
1
1
1
1
0
0
0
0
1
0
1
0
1
~
1
1
1
1
1
1
0
0
0
1
0
1
0
1
0
1
Рисунок
2.12 - Карти Карно для входів
,
,
,
z
Рисунок
2.13 - Карти Карно для входів
,
,
функції виходу z
Після утворення функцій реалізується схема автомата (рисунок 2.14).
2.4 Регістр
Щоб налагодити роботу дискретного пристрою (рисунок 3.1) необхідно співставити між собою виходи АП 1 та АП 2 з відповідними входами дешифраторів. Для цього застосовано регістри (рисунок 2.18), які перетворюють послідовні коди на виходах АП у паралельні для подачі їх на входи дешифраторів.
Регістр зсуву являє собою схему з’єднаних між собою однобітових елементів пам’яті (тригери), що знаходяться в єдиному корпусі. Тригери з’єднані один з одним таким чином, що вихід одного слугують входами другого.
Розрізняють наступні регістри:
-
із зсувом вправо;
-
із зсувом вліво;
-
реверсивні .
В даному випадку застосовано регістр зсуву вліво (рисунок 2.18). Синтезується аналогічно іншим АП.
Рисунок 2.15 – Граф переходів-виходів регістра зсуву вліво
Після утворення графу будується функціональна таблиця (таблиця 2.9).
Таблиця
2.9 – Функціональна таблиця регістра
зсуву вліво
|
t |
t+1 |
Тригери |
z1 |
z2 |
z3 |
||||||||||
|
x |
y1 |
y2 |
y3 |
y1 |
y2 |
y3 |
|
|
|
|
|
|
|||
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
~ |
1 |
~ |
1 |
~ |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
~ |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
~ |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
~ |
1 |
1 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
~ |
1 |
~ |
0 |
0 |
0 |
|
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
0 |
~ |
1 |
1 |
0 |
1 |
~ |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
1 |
1 |
0 |
~ |
1 |
~ |
1 |
1 |
0 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
~ |
1 |
~ |
0 |
1 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
~ |
0 |
1 |
~ |
1 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
~ |
1 |
~ |
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
~ |
0 |
1 |
0 |
0 |
1 |
|
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
~ |
1 |
0 |
1 |
1 |
|
1 |
1 |
1 |
0 |
1 |
0 |
1 |
~ |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
~ |
1 |
~ |
1 |
~ |
1 |
1 |
1 |
1 |
Далі складаються карти Карно для мінімізації функцій входів тригерів (рисунки 2.16 та 2.17).
Рисунок 2.16 – Карти Карно функцій входів тригерів
Рисунок 2.17 – Карти Карно функцій входів тригерів
Після виконання усіх необхідних дій синтезується схема регістру (рисунок 2.18). Значення сигналів на виходах регістру співпадають із значенням сигналів на виходах тригерів.
Рисунок 2.18 – Схема регістра
