Вариант 9

Строительной компании нужно решить задачу о приготовлении не менее 6 т смеси бетона для заливки фундамента. Смесь приготавливается из цемента и гравия. Отношение массы гравия к массе цемента в смеси не должно быть больше, чем 7 : 3. Расход цемента не должен превышать 7 т, а гравия – 16 т. Производственно-технические условия таковы, что на процессы смешивания и заливки фундамента может быть отведено более 18 ч, при этом на 1 т цемента уходит 2 ч, а на 1 т гравия – 3 ч производственного времени. Стоимость 1 т цемента – 13 тыс руб, гравия – 4 тыс руб.

Построить математическую модель задачи, на основании которой можно найти состав смеси при условии минимизации его стоимости.

Вариант 10

Предприятие выпускает продукцию трех видов: П1, П2 и П3. Норма расхода материала М1, М2 и М3 в расчете на одно изделие, плановая себестоимость, оптовая цена предприятия, плановый ассортимент и трудоемкость единицы продукции приведены в табл. При этом запас материала М1, М2 и М3 - 180, 1500 и 124 ед изм соответственно. Плановый фонд рабочего времени 26100 человеко-часов.

Исходя из необходимости выполнения плана по ассортименту и возможности его перевыполнения по отдельным (и даже всем) показателям, построить модель, на основе которой можно найти план производства, максимизирующий прибыль.

Исходные данные варианта 10

Показатели	Изделия
	П1	П2	П3
Норма расхода материала М1, ед изм	0,052	0,034	0,138
Норма расхода материала М2, ед изм	0,120	0,120	0,018
Норма расхода материала М3, ед изм	0,007	0,007	0,008
Трудоемкость, чел-ч	12,3	8,4	6,2
Плановая себестоимость, ден ед	98,81	71,67	31,55
Оптовая цена предприятия, ден ед	102,00	78,00	34,00
Плановый ассортимент, шт	380	310	1250

Задание 2

Решить задачу линейного программирования графическим методом.

Вариант – 1

Z(х)=х₁+х₂+30min

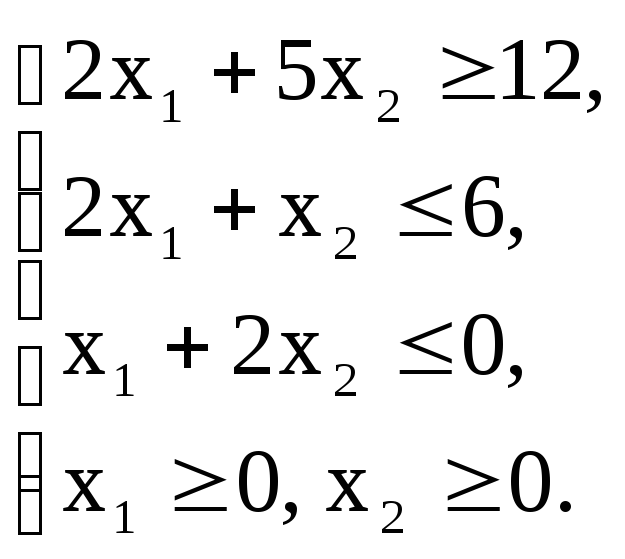
Вариант – 2

Z(х)=2х₁-+20max

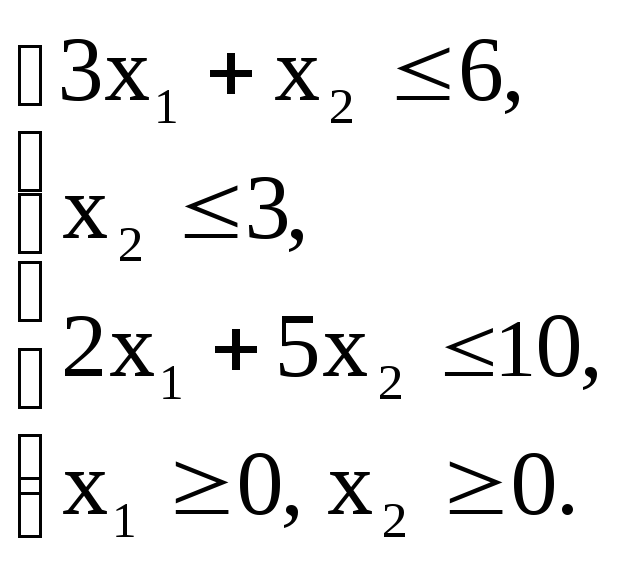
Вариант – 3

Z(х)=37x₁+66x₂+32max

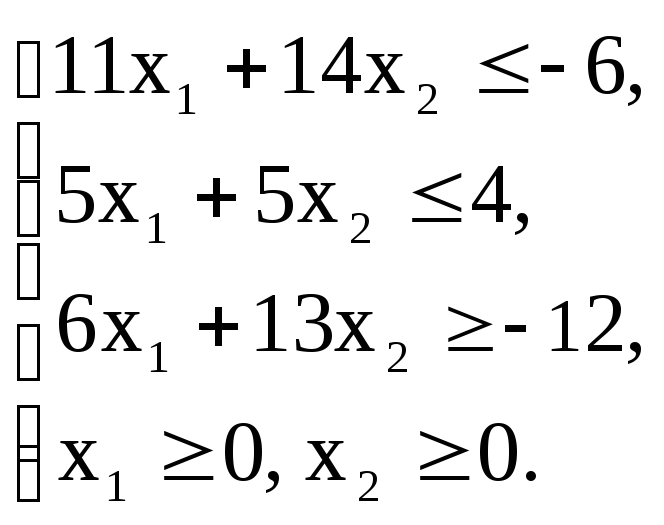
Вариант – 4

Z(х)=-4x₁+x₂+6min

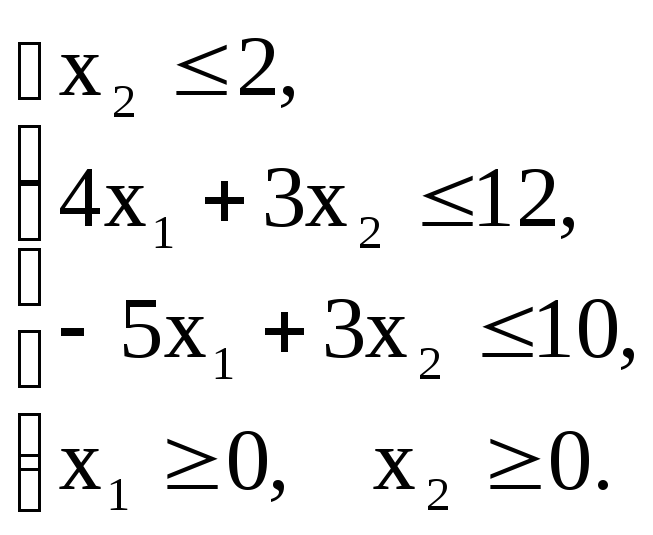
Вариант – 5

Z(х)=-9x₁-9,5x₂+15,5min

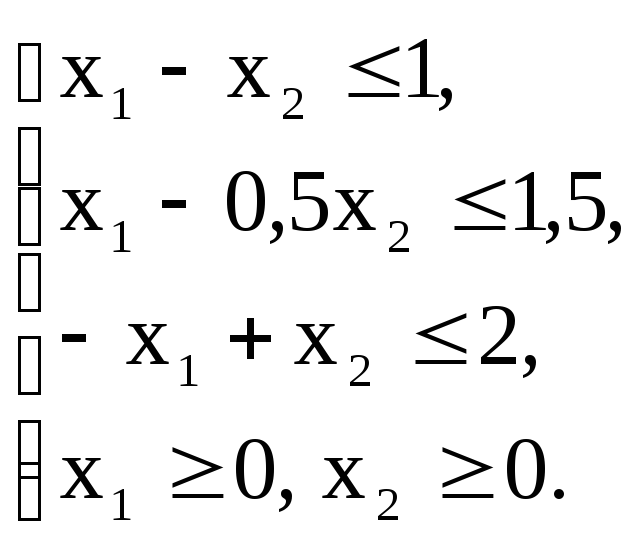
Вариант – 6

Z(х)=12x₁+x₂+12,5max

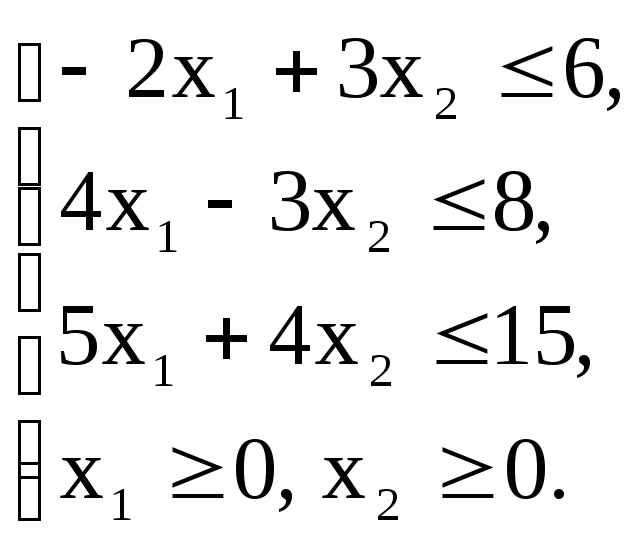
Вариант – 7

Z(х)=-2x₁-5x₂+21max

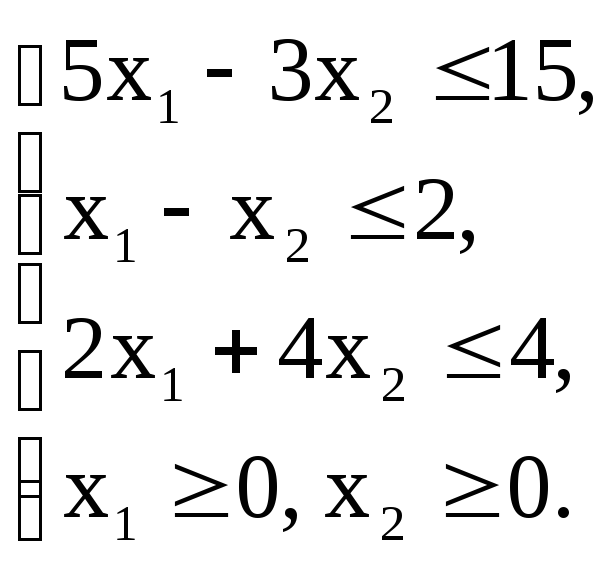
Вариант – 8

Z(х)= -2x₁+x₂+66min

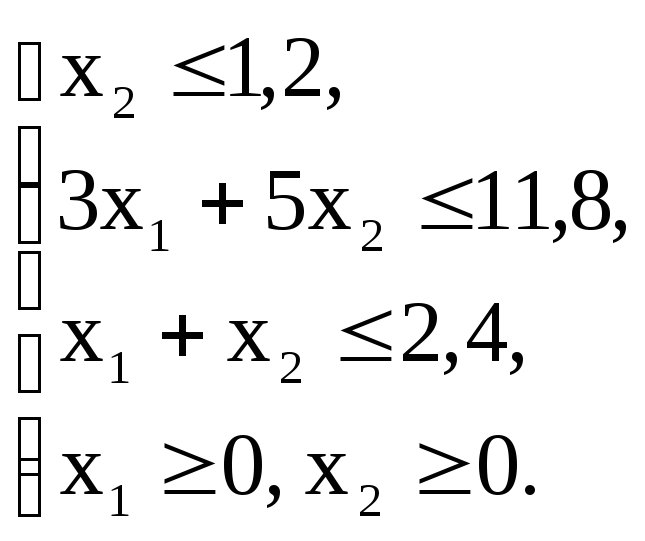
Вариант – 9

Z(х)=2x₁+5x₂+4max

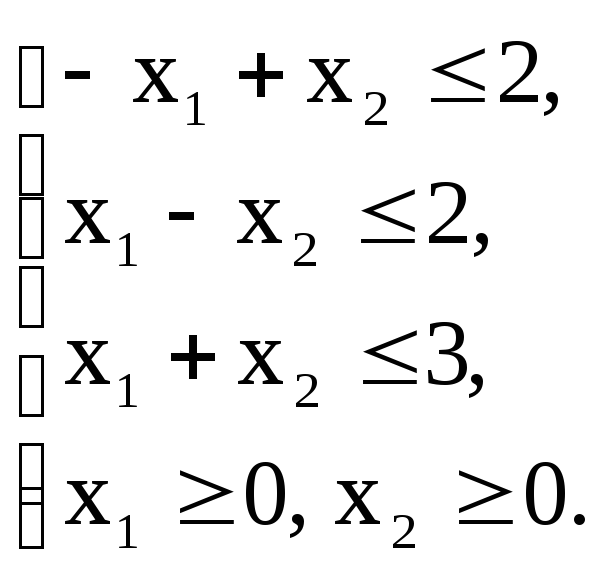
Вариант – 10

Z(х)=x₁+2x₂+12max

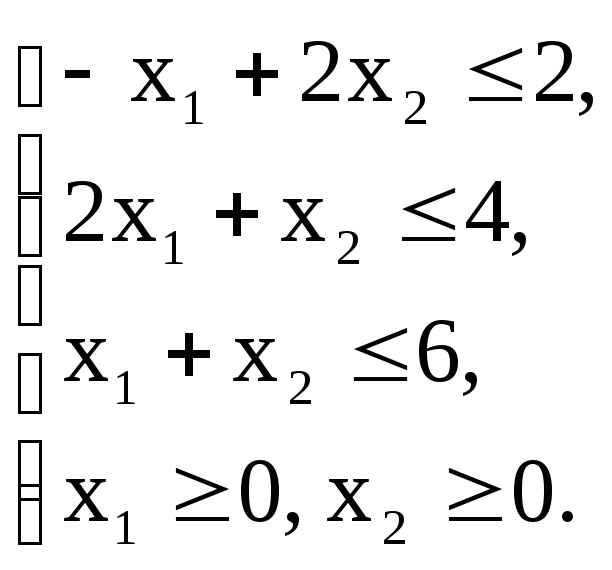
Задание 3

Решить задачу линейного программирования симплекс-

методом.

Вариант – 1

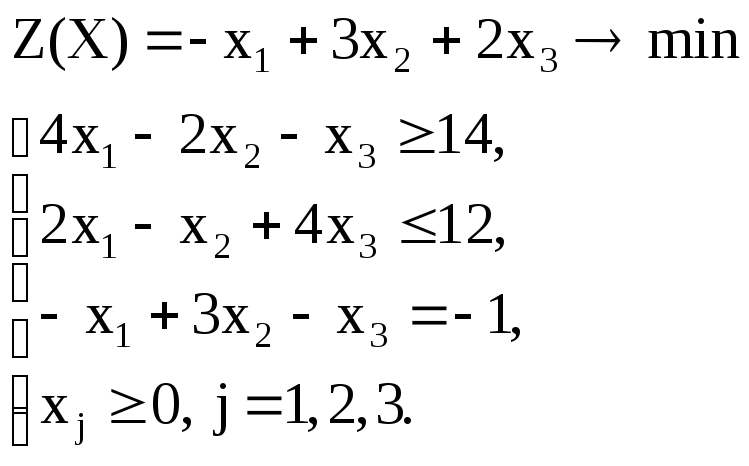
Вариант – 2

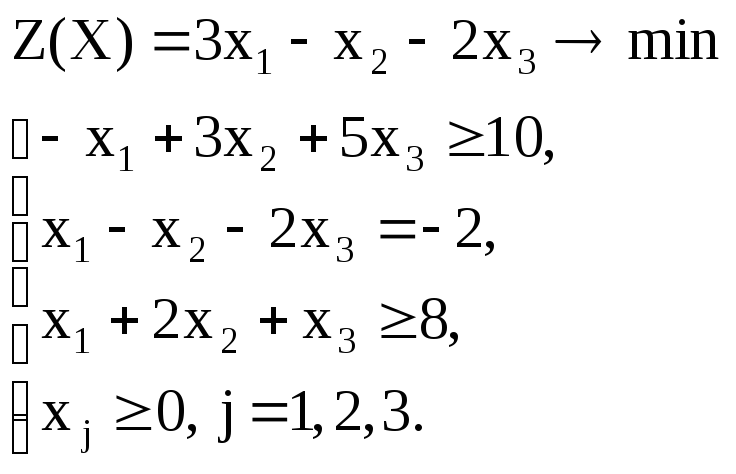
Вариант – 3

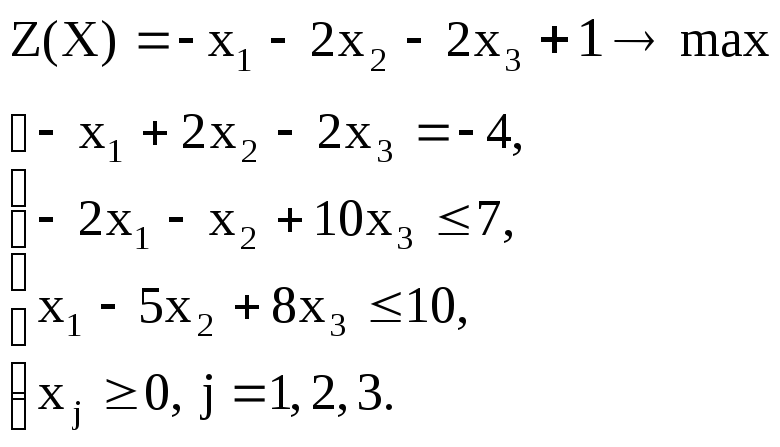
Вариант – 4

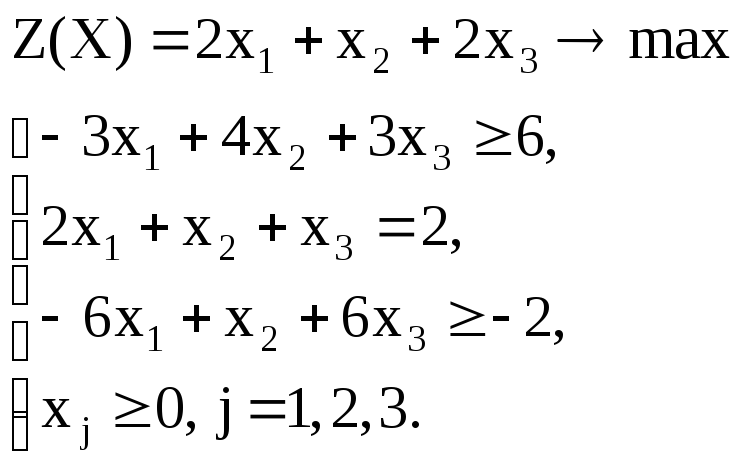
Вариант – 5

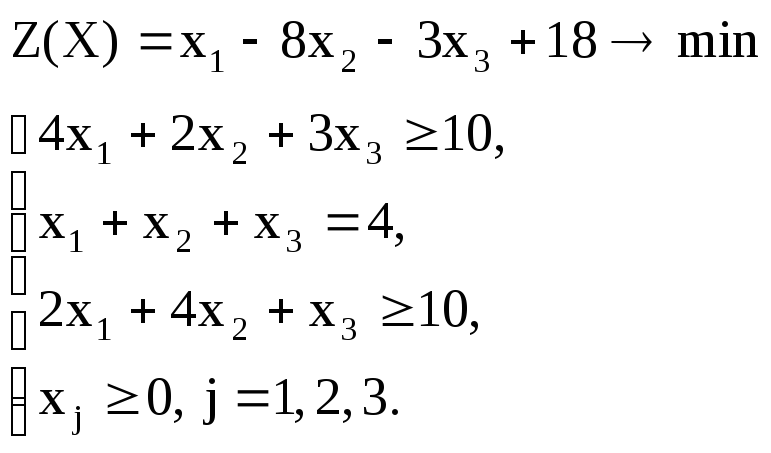
Вариант – 6

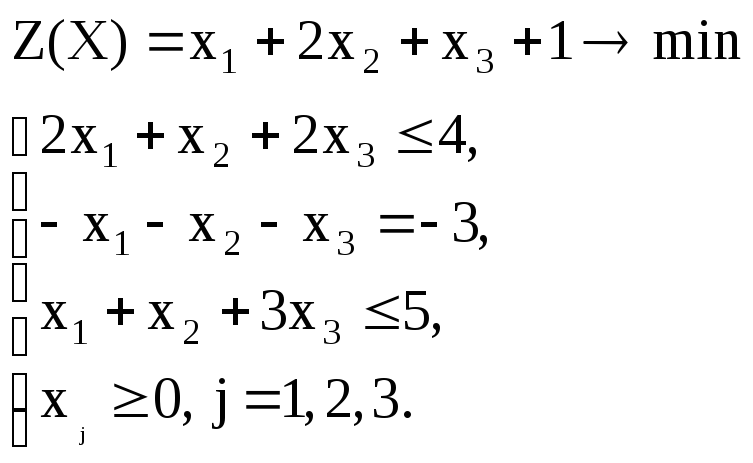
Вариант – 7

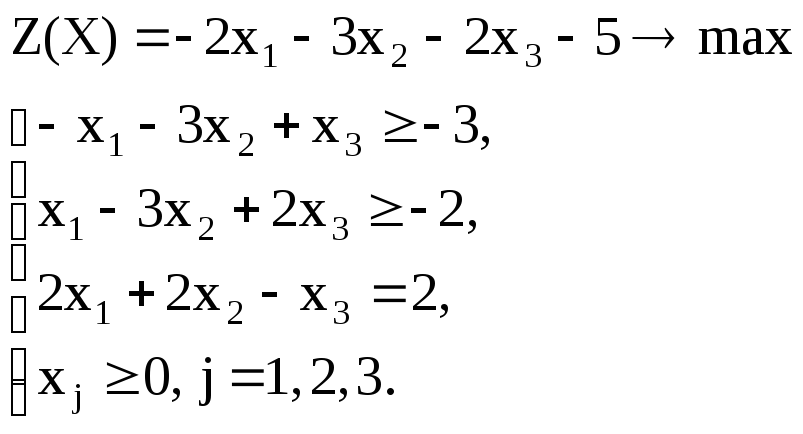
Вариант – 8

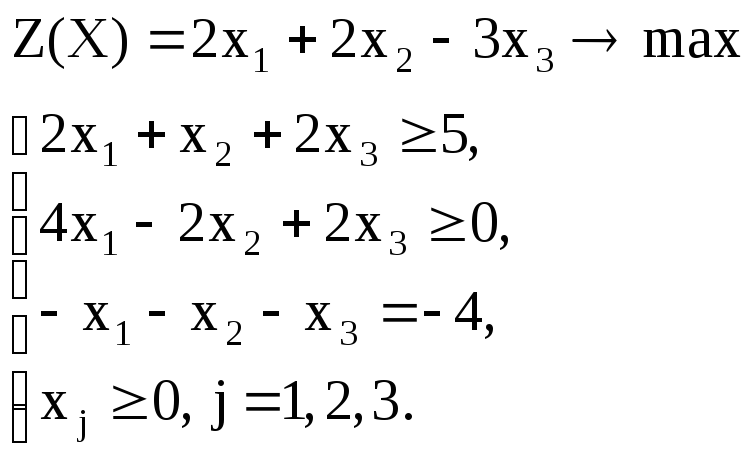
Вариант – 9

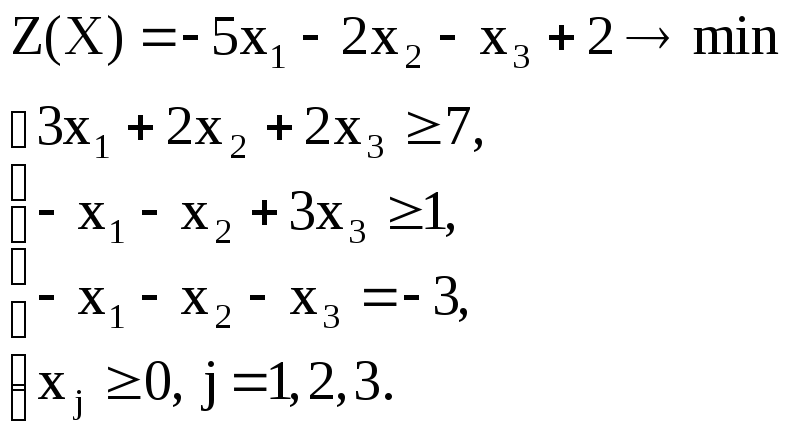
Вариант – 10

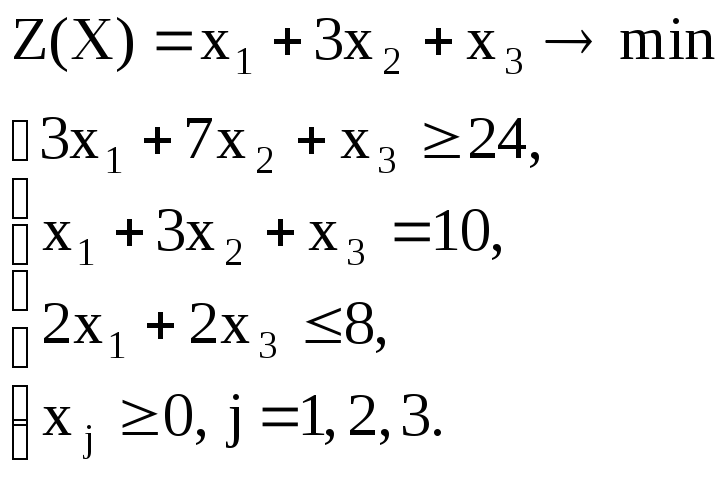
Вариант – 11

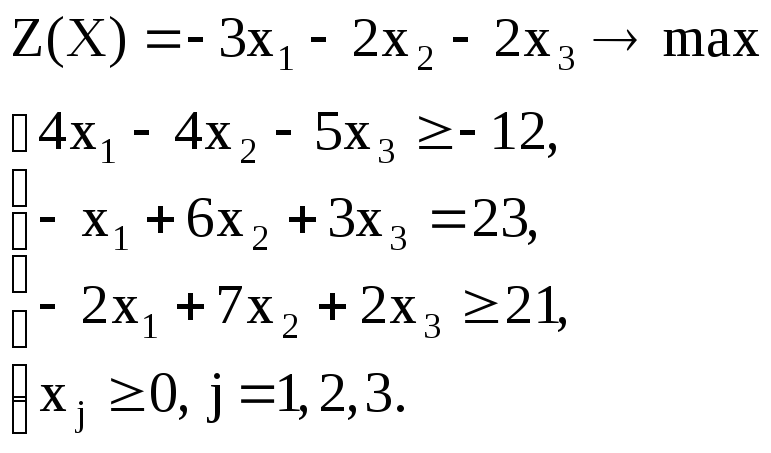
Вариант – 12

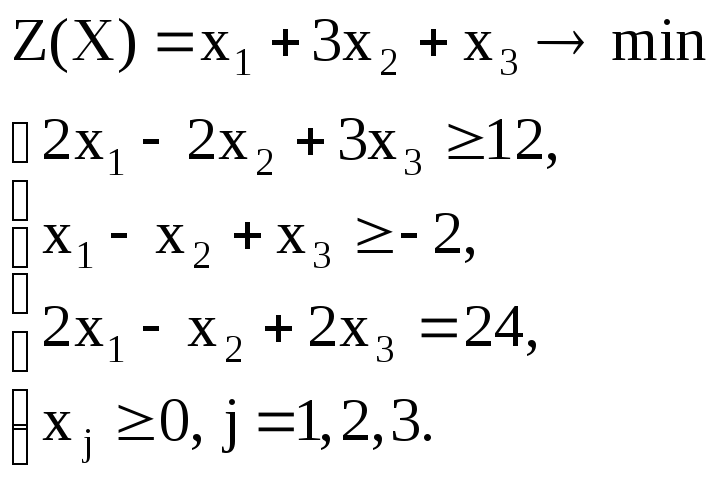
Вариант – 13

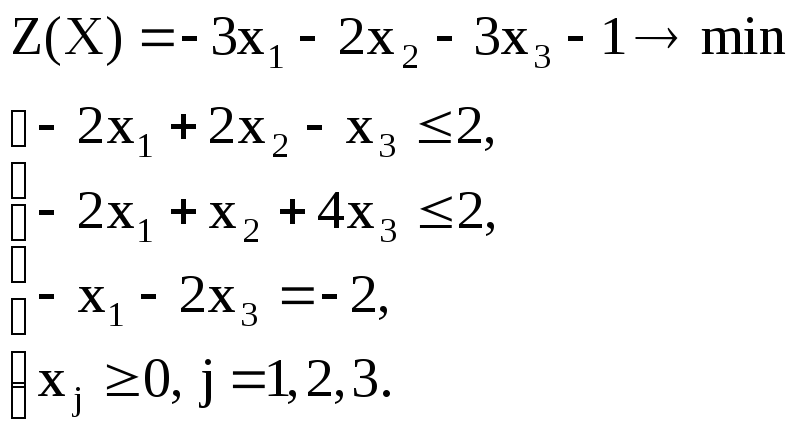
Вариант – 14

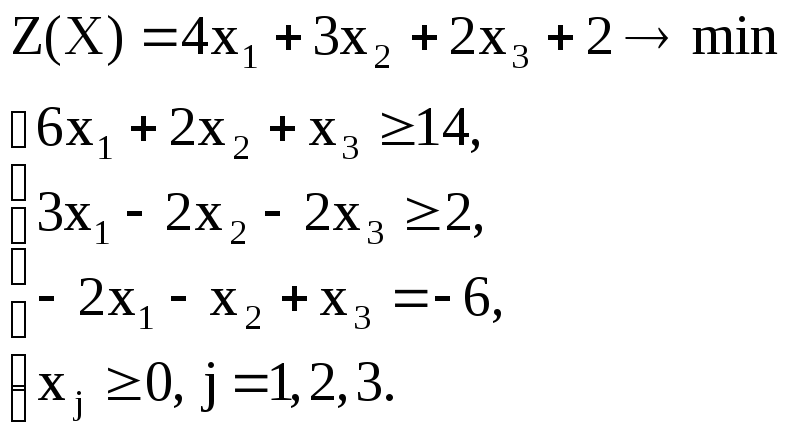
Вариант – 15

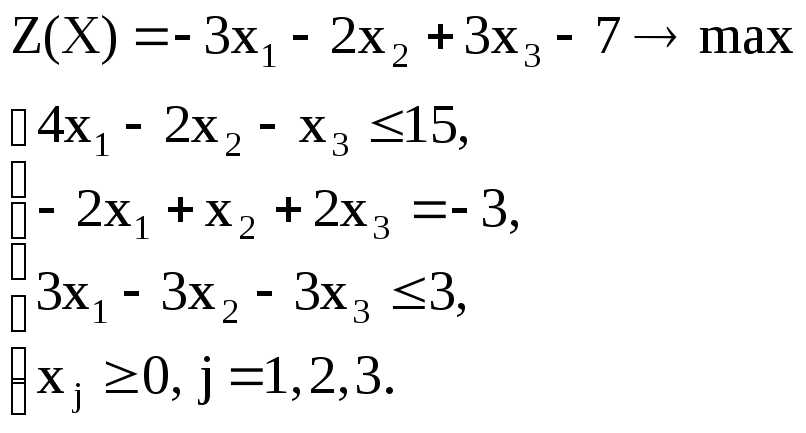
Вариант – 16

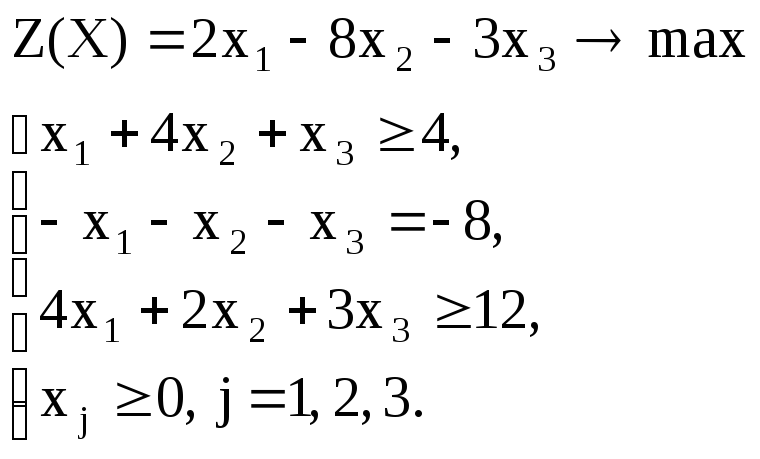
Вариант – 17

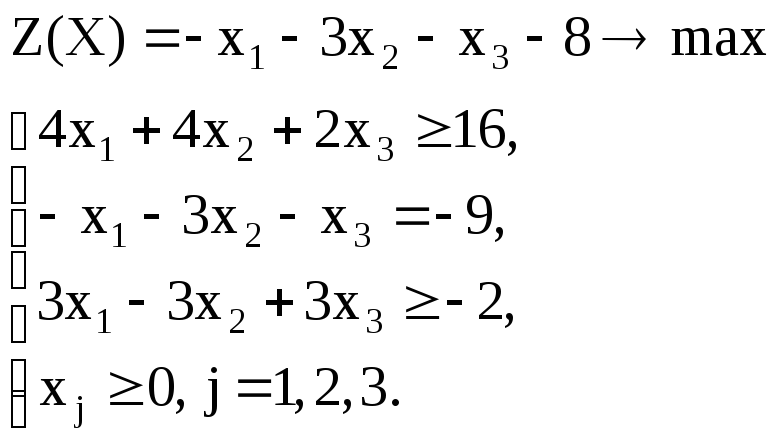
Вариант – 18

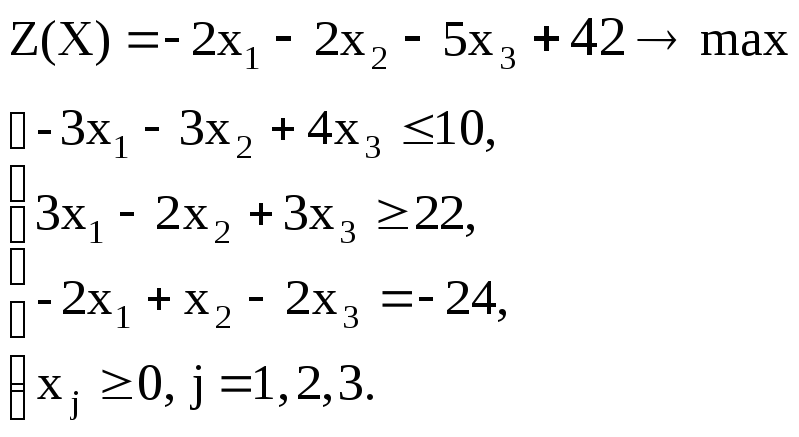
Вариант – 19

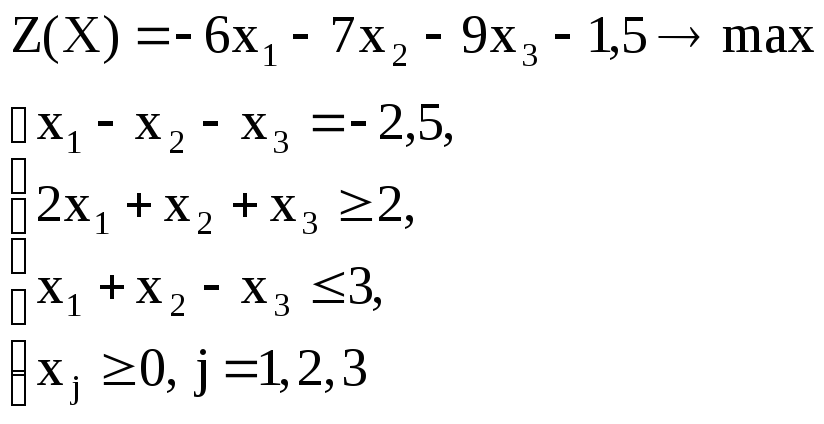
Вариант – 20

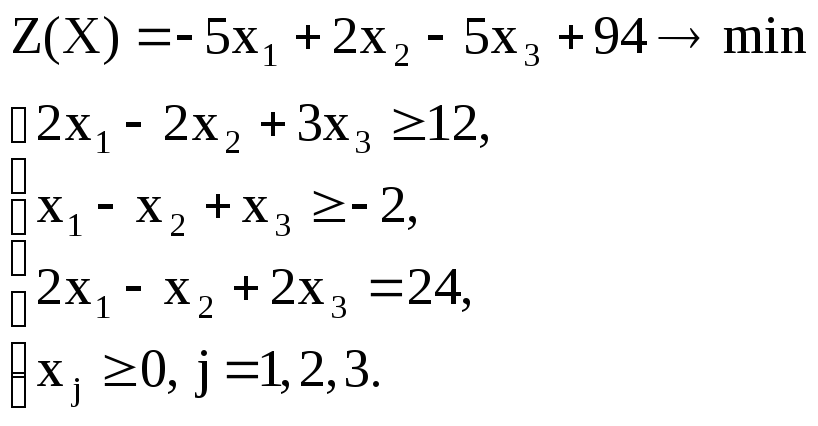
Вариант – 21

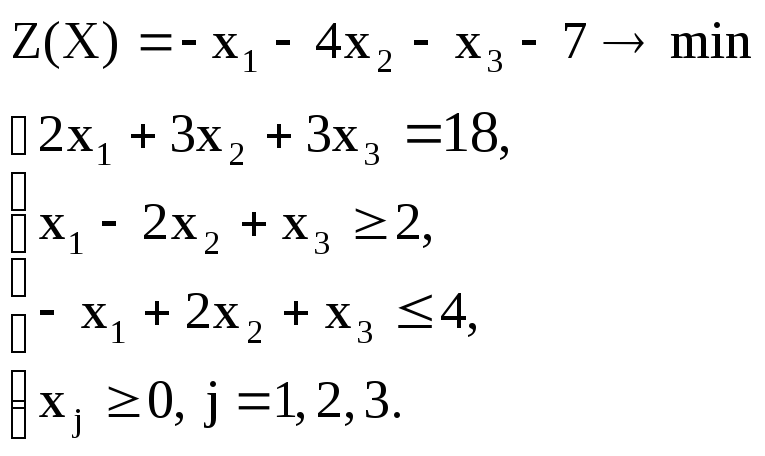
Вариант – 22

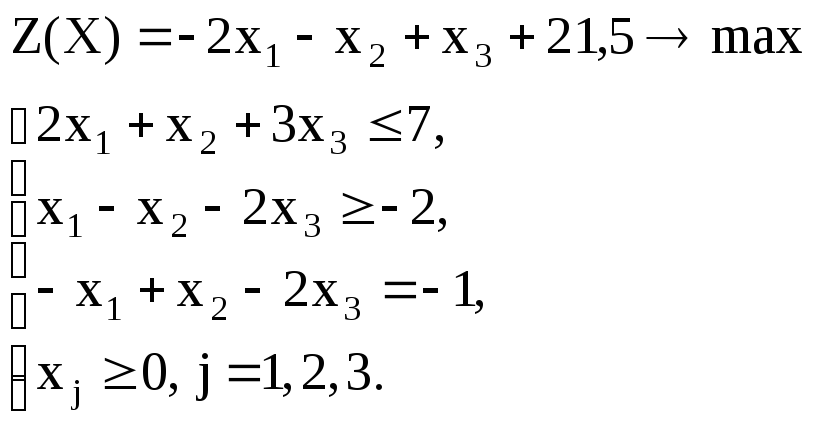
Вариант – 23

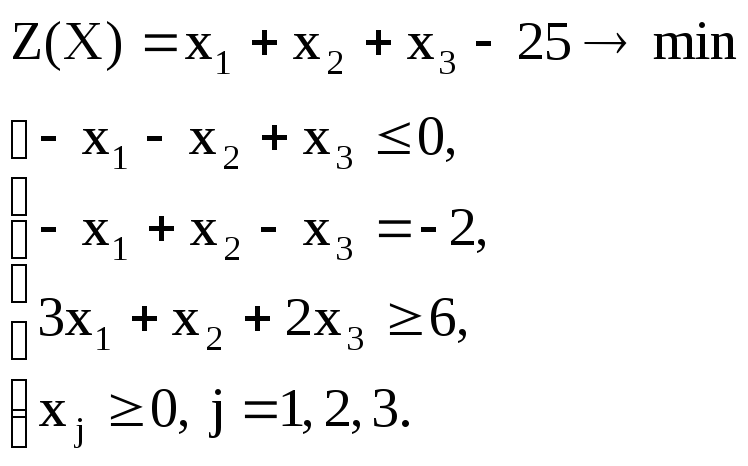
Вариант – 24

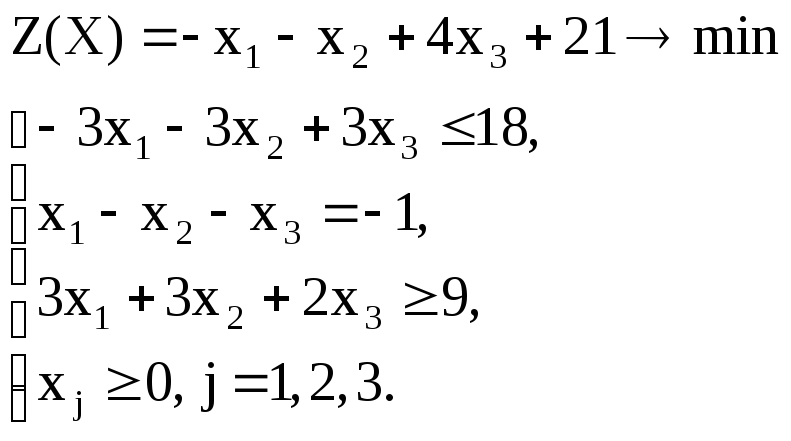
Вариант – 25

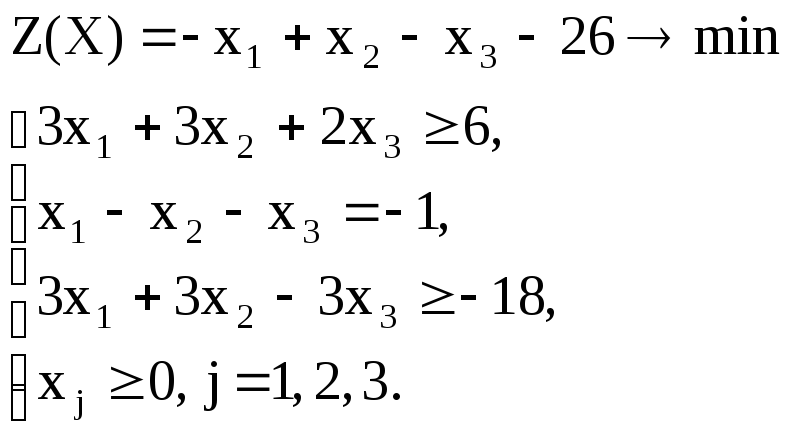
Вариант – 26

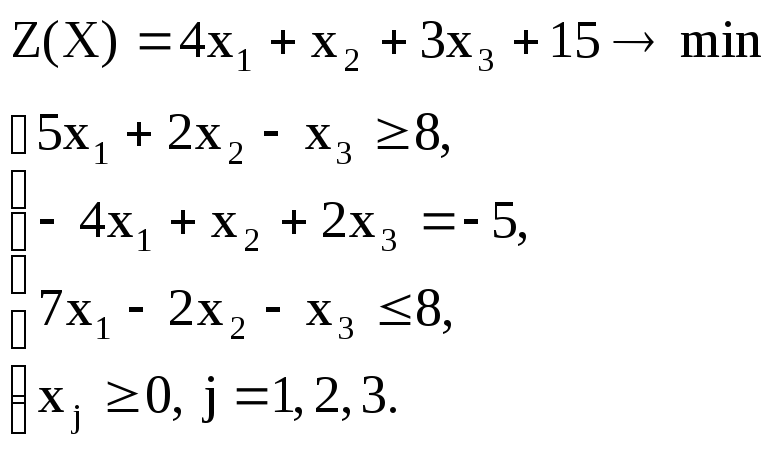
Вариант – 27

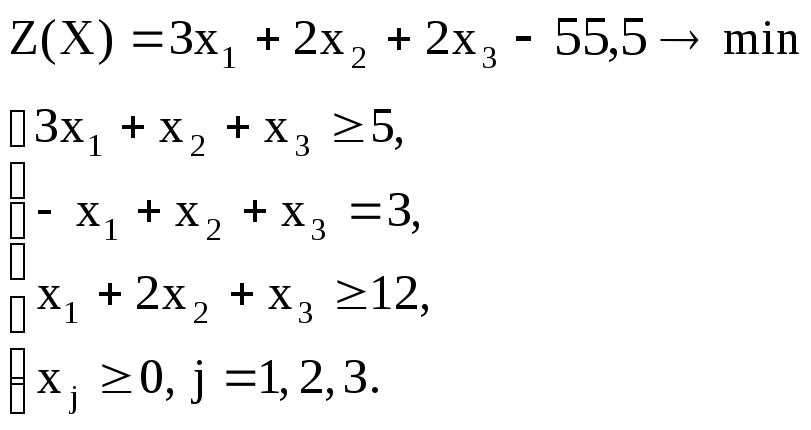
Вариант – 28

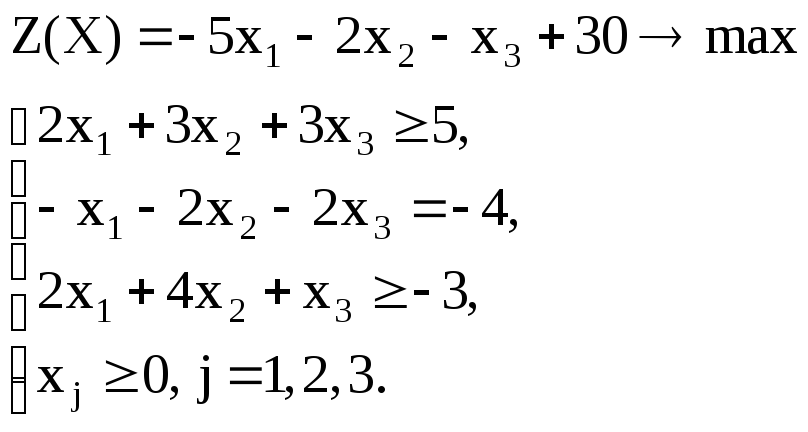
Вариант – 29

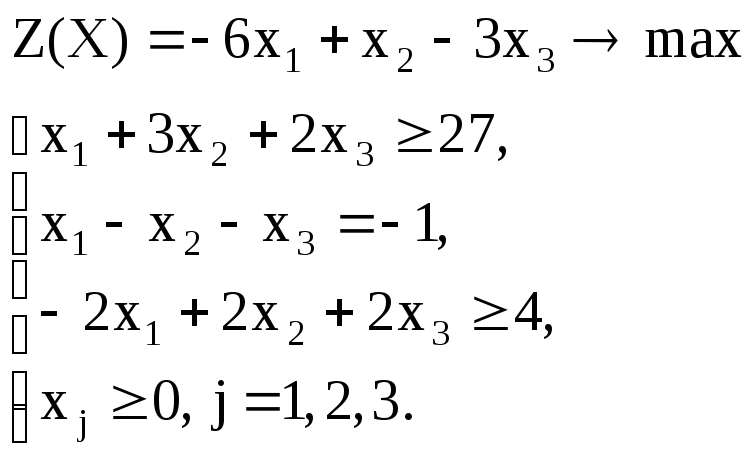
Вариант – 30

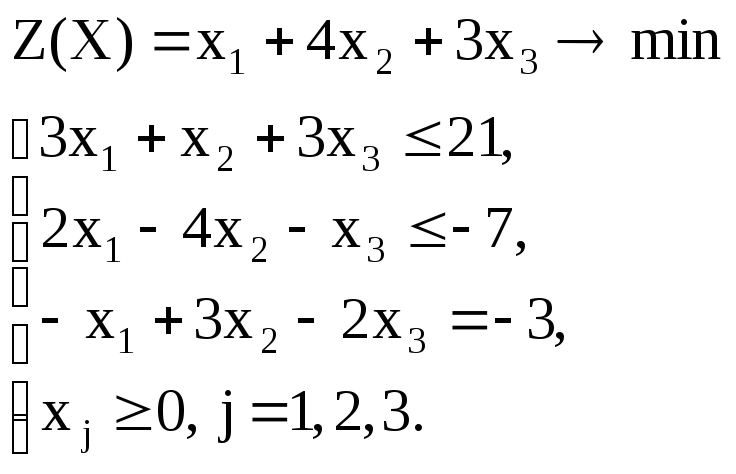
Задание 4

Построить двухиндексную (транспортную) модель задачи линейного программирования, найти опорные планы методами северо-западного угла и минимального элемента. Решить транспортную задачу линейного программирования, используя метод потенциалов.

Составьте план перевозок продуктов из n пунктов отправления (А_i) в m пункты назначения (B_j). План должен обеспечить минимальные транспортные издержки и полностью удовлетворить спрос потребителей на продукты. Запас (а_i), потребность (b_j) и стоимость перевозки 1 единицы измерения продуктов (с_ij) приведены в табл. 1-10.