3. Свойства отношений

Очевидно, что произвольные бинарные отношения изучать в общем плане не особенно интересно, о них можно сказать очень мало. Однако, если отношения удовлетворяют некоторым дополнительным условиям, относительно них можно делать более содержательные утверждения. В этом разделе мы рассмотрим некоторые из основных свойств бинарных отношений.

Определение 3.1. Бинарное отношение  на множестве X называется рефлексивным, если для любого элемента aX выполняется условие a a:

( aX) a a.

Если отношение представлено с помощью графа, то рефлексивность этого отношения означает, что в каждой вершине графа обязательно имеется петля.

Для отношения, заданного с помощью булевой матрицы его рефлексивность равносильна тому, что по главной диагонали этой матрицы (идущей из ее левого верхнего угла в правый нижний) стоят только символы 1.

Определение 3.2. Бинарное отношение  на X называется антирефлексивным, если ни для одного aX не выполняется условие a  a:

( aX) .

Обозначим через I_x отношение на множестве X, состоящее из пар вида (a, a), где a X:

I_x = {(a, a)| a X}.

Отношение I_x обычно называют диагональю множества X или отношением тождества на X.

Очевидно, что отношение  на множестве X рефлексивно, если диагональ I_x является подмножеством множества  :

I_x  .

Отношение антирефлексивно, если диагональ I_x и отношение  не имеют ни одного общего элемента:

I_x   = O.

Определение 3.3. Бинарное отношение  на множестве X называется симметричным, если из a  b следует b  a:

( a, bX)(a b ba).

Примерами симметричных отношений являются:

• отношение перпендикулярности на множестве прямых;

• отношение касания на множестве окружностей;

• отношение "быть похожим" на множестве людей;

• отношение "иметь одинаковый пол" на множестве животных.

Отношение "x брат y" на множестве всех людей не является симметричным. В то же время отношение "x брат y" на множестве мужчин симметричным является.

В графе симметричного отношения для каждой дуги из вершины x в вершину y имеется дуга из y в x. Поэтому симметричные отношения можно представлять графами с неориентированными ребрами. При этом каждая пара ориентированных ребер xy и yx заменяется одним неориентированным ребром.

На рисунке 8 представлено отношение

= {(a, b), (b, a), (b, c), (c, b), (d, c)}

с помощью ориентированного и неориентированного графов.

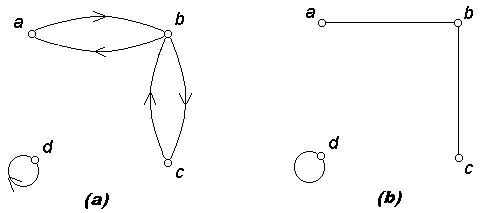
Рис. 8. Представление симметричного отношения с помощью ориентированного (a) и неориентированного (b) графов

Матрица симметричного отношения симметрична относительно главной диагонали.

Теорема 3.1. Объединение и пересечение любого семейства симметричных отношений снова являются симметричными отношениями.

Определение 3.4. Бинарное отношение на множестве X называется антисимметричным, если для любых различных элементов a и b условия a  b и b  a не выполняются одновременно:

( a, bX) (a  b & b a    a = b).

Например, отношение "делится" на множестве натуральных чисел является антисимметричным, так как из a b и b a следует, что a = b. Однако на множестве целых чисел отношение "делится" антисимметричным не является, так как (-2)  2 и 2    (-2), но

-22.

Отношения "выше", "тяжелее", "старше" антисимметричны на множестве людей. Отношение "быть сестрой" на множестве всех людей антисимметричным не является.

В графе антисимметричного отношения две различные вершины могут быть соединены не более чем одной дугой.

Определение 3.5. Бинарное отношение a на множестве X называется транзитивным, если для любых трех элементов a, b, c  X из ab и bc следует ac:

( a, b, c  X) (a b & b c ac).

Примерами транзитивных отношений служат:

• отношение "делится" на множестве действительных чисел;

• отношение "больше" на множестве действительных чисел;

• отношение "старше" на множестве людей игрушек;

• отношение "иметь одинаковый цвет" на множестве детских игрушек;

д) отношение "быть потомком" на множестве людей.

Феодальное отношение "быть вассалом" не является транзитивным. Это в частности подчеркивается в некоторых учебниках истории: "вассал моего вассала не мой вассал".

Отношение "быть похожим" на множестве людей не обладает свойством транзитивности.

Для произвольного отношения  можно найти минимальное транзитивное отношение 

такое, что. Минимальность отношения понимается в том смысле, что для любого транзитивного отношения из  следует. Таким отношением является транзитивное замыкание отношения .

Пример 3.1. Транзитивным замыканием бинарного отношения на множестве людей "быть ребенком" является отношение "быть потомком".

Справедлива теорема.

Теорема 3.2. Для любого отношения транзитивное замыкание равно пересечению всех транзитивных отношений, включающих в качестве подмножества.

Определение 3.6. Бинарное отношение  на множестве X называется связным, если для любых двух различных элементов a и b имеет место ab, либо ba:

(   a, b, c  X)(ab  ab  ba).

Примером связного отношения является отношение "больше" на множестве действительных чисел. Отношение "делится" на множестве целых чисел связным не является.