комплексные числа

§1. Комплексные числа

1°. Определение. Алгебраическая форма записи.

Определение 1. Комплексными числами называются упорядоченные пары действительных чисел и , если для них определены понятие равенства, операции сложения и умножения, удовлетворяющие следующим аксиомам:

1) Два числа и равны тогда и только тогда, когда , , т.е.

, .

(1)

2) Суммой комплексных чисел и называется число, обозначаемое и равное , т.е.

+=.

(2)

3) Произведением комплексных чисел и называется число, обозначаемое и равное , т.е.

∙=.

(3)

Множество комплексных чисел обозначается C.

Формулы (2),(3) для чисел вида принимают вид

,

откуда следует, что операции сложения и умножения для чисел вида совпадают со сложением и умножением для вещественных чисел  комплексное число вида отождествляется с вещественным числом .

Комплексное число называется мнимой единицей и обозначается , т.е. Тогда из (3) 

Из (2),(3)  что и значит

(4)

Выражение (4) называется алгебраической формой записи комплексного числа.

В алгебраической форме записи операции сложения и умножения принимают вид:

.

Комплексное число обозначают , – вещественная часть, – мнимая часть, – чисто мнимое число. Обозначение: , .

Определение 2. Комплексное число называется сопряженным с комплексным числом .

Свойства комплексного сопряжения.

1)

2) .

3) Если , то .

4) .

5) – вещественное число.

Доказательство проводится непосредственным вычислением.

Определение 3. Число называется модулем комплексного числа и обозначается .

Очевидно, что , причем . Также очевидны формулы: и .

2°. Свойства операций сложения и умножения.

1) Коммутативность: , .

2) Ассоциативность:, .

3) Дистрибутивность: .

Доказательство 1) – 3) проводится непосредственными вычислениями на основе аналогичных свойств для вещественных чисел.

4) , .

5) , C ! , удовлетворяющее уравнению . Такое

.

6) ,C, 0, ! : . Такое находится умножением уравнения на .

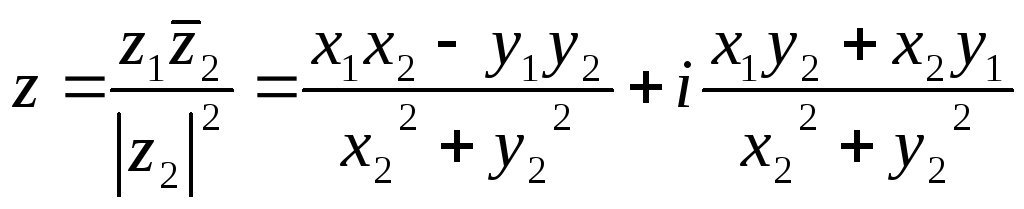Пример. Представим комплексное число в алгебраической форме. Для этого умножим числитель и знаменатель дроби на число, сопряженное знаменателю. Имеем:

3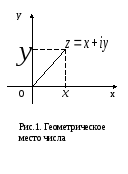°. Геометрическая интерпретация комплексных чисел. Тригонометрическая и показательная форма записи комплексного числа.

Пусть на плоскости задана прямоугольная система координат. Тогда C можно поставить в соответствие точку на плоскости с координатами .(см. рис. 1). Очевидно, что такое соответствие является взаимно однозначным. При этом действительные числа лежат на оси абсцисс, а чисто мнимые ­− на оси ординат. Поэтому ось абсцисс называют действительной осью, а ось ординат − мнимой осью. Плоскость, на которой лежат комплексные числа, называется комплексной плоскостью.

Отметим, что и симметричны относительно начала координат, а и симметричны относительно Ox.

Каждому комплексному числу (т.е. каждой точке на плоскости) можно поставить в соответствие вектор с началом в точке O и концом в точке . Соответствие между векторами и комплексными числами является взаимно однозначным. Поэтому вектор, соответствующий комплексному числу , обозначается той же буквой

Длина вектора соответствующего комплексному числу , равна , причем , .

С помощью векторной интерпретации можно видеть, что вектор − сумма векторов и , а − сумма векторов и .(см. рис. 2). Поэтому справедливы неравенства: ,

.

Наряду с длиной вектора введем в рассмотрение угол между вектором и осью Ox, отсчитываемый от положительного направления оси Ox: если отсчет ведется против часовой стрелки, то знак величина угла рассматривается положительной, если по часовой стрелке – то отрицательной. Этот угол называется аргументом комплексного числа и обозначается . Угол определяется не однозначно, а с точностью … . Для аргумент не определяется.

При этом

, .

(5)

Следовательно, любое комплексное число можно представить в виде

.

(6)

Формулы (6) задают так называемую тригонометрическую форму записи комплексного числа.

Из (5) следует, что если и то

, .

(7)

Из (5) что по и комплексное число определяется однозначно. Обратное неверно: а именно, по комплексному числу его модуль находится однозначно, а аргумент, в силу (7), − с точностью . Также из (7) следует, что аргумент может быть найден как решение уравнения

Однако не все решения этого уравнения являются решениями (7).

Среди всех значений аргумента комплексного числа выбирается одно, которое называется главным значением аргумента и обозначается . Обычно главное значение аргумента выбирается либо в интервале , либо в интервале

В тригонометрической форме удобно производить операции умножения и деления.

Теорема 1. Модуль произведения комплексных чисел и равен произведению модулей, а аргумент – сумме аргументов, т.е.

, а .

Аналогично

,

Доказательство. Пусть , . Тогда непосредственным умножением получаем:

.

Аналогично

.■

Следствие (формула Муавра). Для справедлива формула Муавра

.

П

y

ример. Пусть Найдем геометрическое местоположение точки . Из теоремы 1 следует, что .

Поэтому для ее построение необходимо вначале построить точку , являющуюся инверсией относительно единичной окружности, а затем найти точку, симметричную ей относительно оси Ox.

Пусть , т.е. Комплексное число обозначается , т.е. R справедлива формула Эйлера

(8)

Так как , то , . Из теоремы 1 что с функцией можно работать как с обычной показательной функцией, т.е. справедливы равенства

, , .

Из (8) показательная форма записи комплексного числа

, где ,

Пример. .

4°. Корни -ой степени из комплексного числа.

Рассмотрим уравнение

, С, N.

(9)

Пусть , а решение уравнения (9) ищется в виде . Тогда (9) принимает вид , откуда находим, что , , т.е.

, , .

Таким образом, уравнение (9) имеет корни

, .

(10)

Покажем, что среди (10) имеется ровно различных корней. Действительно, различны, т.к. их аргументы различны и отличаются меньше, чем на . Далее, , т.к. . Аналогично .

Таким образом, уравнение (9) при имеет ровно корней , расположенных в вершинах правильного -угольника, вписанного в окружность радиуса с центром в т. O.

Таким образом, доказана

Теорема 2. Извлечение корня -ой степени из комплексного числа всегда возможно. Все значения корня -ой степени из расположены в вершинах правильного -угольника, вписанного в окружность с центром в нуле и радиуса . При этом,

.

Следствие. Корни –ой степени из 1 выражаются формулой

.

Произведение двух корней из 1 является корнем, 1 – корень -ой степени из единицы, корня : .