лаба 21

Министерство образоавния и науки рф

Башкирский государственный университет

Моделирование электростатических полей систем зарядов

Методические указания к выполнению лабораторной работы №21 по курсу общей физики «Электричество»

для студентов физического факультета

МОДЕЛИРОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ СИСТЕМ ЗАРЯДОВ

Цель работы: исследовать двумерную структуру полей, образованных, следующими источниками: системой из четырех зарядов, произвольных по величине и расположению в плоскости; диполем; квадруполем; линейным квадруполем.

Приборы и принадлежности: компьютер, снабженный программой моделирующей электрические поля неподвижных зарядов путем построения силовых и эквипотенциальных линий в плоскости дислокации данных зарядов.

Краткая теория

Расчет электростатических полей представляет собой важную прикладную задачу.

Электростатическое поле точечного заряда q в вакууме характеризуется вектором напряженности и потенциалом :

, _,

где - радиус-вектор, проведенный от заряда в точку наблюдения, q- заряд, создающий электрическое поле, =8,85x10^-12 Ф/м - электрическая постоянная.

Напряженность электрического поля является основной количественной характеристикой поля, она определяется отношением силы, действующей со стороны поля на электрический заряд q, к величине этого заряда (при этом заряд должен быть малым, чтобы не изменять ни величины, ни распределения тех зарядов, которые порождают исследуемое поле).

В вакууме напряженность электрического поля системы точечных зарядов удовлетворяет принципу суперпозиции, согласно которому полная напряженность поля в некоторой точке равна векторной сумме напряженностей полей, создаваемых в этой точке каждым зарядом в отдельности:

, (1)

где N - число зарядов.

Потенциал φ произвольной точки поля нескольких зарядов равен алгебраической сумме потенциалов, создаваемых в этой точке каждым зарядом в отдельности:

. (2)

При этом точка нулевого потенциала выбирается общей для всех зарядов. Принцип суперпозиции фактически означает, что присутствие других зарядов никак не сказывается на поле, создаваемом данным зарядом.

Для электрических полей существует связь между вектором напряженности и потенциалом φ: . Отметим, что в системе СИ величина измеряется в В/м, a φ в В.

Силовые линии вектора - это воображаемые линии, которые проводят таким образом, что касательная к ним в каждой точке пространства совпадает по направлению с вектором, характеризующим данное поле - вектором . Поскольку напряженность поля - однозначная функция координат точки пространства, то через каждую точку может проходить только одна силовая линия. Густота силовых линий обычно выбирается так, чтобы число силовых линий, проходящих через единичную площадку, перпендикулярную к силовой линии, была пропорциональна напряженности поля. Поэтому силовые линии дают наглядную картину распределения поля в пространстве: они начинаются на положительных зарядах и оканчиваются на отрицательных (или уходят в бесконечность). Поверхность, все точки которой имеют один и тот же потенциал, называется эквипотенциальной. Выражения (1) и (2) можно использовать для непосредственных вычислений силовой () и энергетической (φ) характеристик электрического поля. Как уже говорилось выше, их можно изображать либо с помощью силовых линий, либо с помощью эквипотенциальных поверхностей. Силовые линии перпендикулярны поверхности постоянного потенциала: имея одну из этих картин, легко можно построить другую. Силовые линии уединенного точечного заряда представляют собой симметрично расположенные радиальные прямые, а эквипотенциальные поверхности - концентрические сферы с общим центром в точке расположения точечного заряда.

При рассмотрении электрического поля, создаваемого системой зарядов на больших по сравнению с линейными размерами этой системы расстояниях, можно получить весьма простые приближенные формулы для вычисления напряженности поля и потенциала.

Электрическое действие заряженного тела на относительно большом расстоянии определяется полным зарядом этого тела q. Чем дальше от тела, тем меньше отличается созданное им электрическое поле от поля точечного заряда: это поле обладает сферической симметрией, его потенциал убывает с расстоянием как 1/г, а напряженность поля -как 1/r². Таким образом, тело со сложным распределением заряда, полная величина которого равна q, на достаточно большом расстоянии кажется просто точечным зарядом. В этом легко можно будет убедиться, пользуясь установленной в компьютере программой, строящей картины эквипотенциальных поверхностей и силовых линий от произвольной системы зарядов, когда их сумма отлична от нуля (пример- рис1).

Рис. 1. Электрическое поле четырех близко расположенных зарядов.

Если полный заряд тела равен нулю, то на больших расстояниях от него электрическое поле подобно полю диполя: потенциал поля обратно пропорционален квадрату, а напряженность поля - кубу расстояния от тела. Поле такого заряженного тела обладает аксиальной симметрией относительно направления электрического дипольного момента , определяемого соотношением:

где - радиус-векторы отдельных зарядов. В случае, когда полный заряд тела равен нулю (), дипольный момент системы не зависит от выбора начала системы координат. Действительно, радиус – векторы и одного и того же заряда в двух разных системах координат связаны друг с другом соотношением:

,

где - некоторый постоянный вектор. Поэтому дипольный момент в обеих системах одинаков:

.

В частности, для системы двух зарядов противоположного знака (q) дипольный момент =q где – радиус - вектор от заряда -q к заряду +q. Такая система зарядов называется диполем (рис. 2, 3).

Рис. 2. К определению потенциала поля диполя в точке А

Рис. 3. Напряженность поля диполя.

Если полный заряд системы равен нулю, то потенциал ее поля на больших расстояниях r дается выражением:

(3)

Напряженность поля при этом может быть представлена как век­торная сумма двух взаимно перпендикулярных составляющих, одна из которых, , направлена вдоль радиус-вектора , характеризующего положение точки А (рис.3) относительно центра диполя, а другая , перпендикулярна ей:

Для величин и справедливы соотношения

, (4)

, (5)

Эти формулы позволяют представить себе картину силовых линий электрического поля диполя. В точке , лежащей на оси диполя (где угол равен нулю или ) , =0 и вектор напряженности направлен вдоль этой оси. Из формулы (4) видно, что его направление совпадает с направлением вектора дипольного момента, как при =0, так и при =. Действительно, при = отрицательно, но при этом следует учесть, что радиус-вектор , на который проектируется вектор , направлен в сторону, противоположную .

Рис. 4. Картина электрического поля от двух разноименных

зарядов на экране.

Во всех точках плоскости, перпендикулярной оси диполя и проходящей через его середину, для которых = радиальная составляющая _г обращается в нуль. Напряженность поля в этих точках перпендикулярна плоскости и направлена в сторону, противоположную вектору дипольного момента . Картина силовых линий для поля диполя, определяемая приближенными формулами (3)-(5), показана на рис.4.

Интересно пронаблюдать, как возникает показанная на рис.4 картина электрического поля диполя. Для этого следует взять два точечных заряда +q и -q на расстоянии друг от друга и с помощью точных формул, заложенных в программу, построить картину эквипотенциальных поверхностей и силовых линий сначала вблизи одного из зарядов, а затем на расстояниях rl.

В первом случае получится картина поля, создаваемого одним то­чечным зарядом , слегка искаженная действием второго заряда. Во втором случае картина силовых линий будет похожа на картину, изображенную на рис. 4. В целом картина электрического поля от двух разноименных зарядов показана на рис.5. Если и полный заряд, и дипольный момент системы зарядов равны нулю, то создаваемое электрическое поле определяется так называемым квадрупольным электрическим моментом системы.

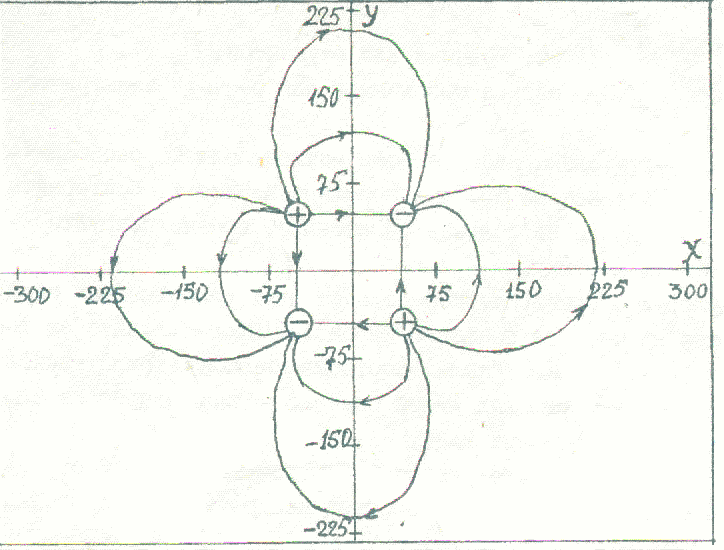
Рис. 5. Электрическое поле квадруполя.

В общем случае потенциал электрического поля на расстоянии r от системы зарядов может быть представлен в виде разложения по степеням 1/г:

Первый член φ⁽⁰⁾ определяется суммой всех зарядов, второй φ⁽¹⁾ -дипольным моментом системы и т.д. При этом член φ^(N) пропорционален 1/rⁿ⁺¹. Это можно проиллюстрировать, пользуясь приведенной ниже программой.

Задания для студентов

1. Научитесь пользоваться компьютерной программой для моделирования электростатических полей.

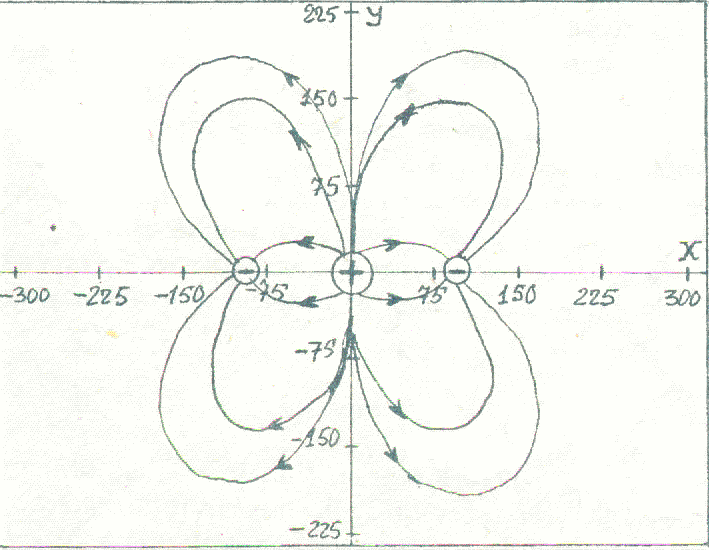
Рис. 6. Электрическое поле линейного квадруполя.

2. Смоделируйте электрическое поле четырех близко расположенных зарядов, похожее на то, что показано на рис.1. Постарайтесь развести заряды на большее расстояние и проанализируйте полученную картину.

3. Смоделируйте электрическое поле от двух разноименных зарядов, похожее на то, что показано на рис. 4. Пронаблюдайте за тем, как возникает поле диполя, построив картину эквипотенциальных поверхностей и силовых линий сначала вблизи одного из зарядов, а затем на расстоянии rl.

4. Смоделируйте поле квадруполя (2 положительных и 2 отрицательных одинаковых заряда на вершинах квадрата ) на расстояниях rl (рис. 5).

5. Смоделируйте поле линейного квадруполя при rl., преобразуя его из обычного квадруполя (рис. 6).

Заметим, что картины силовых линий и эквипотенциальных линий для вышеназванных систем зарядов должны быть помещены в отчет по данной работе.

Контрольные вопросы

1. Дайте определение потенциальным и вихревым полям, приведите примеры этих полей.

2. Как определить потенциал поля объемных зарядов, если известно их расположение в пространстве?

3. Дайте определение напряженности электрического поля в произвольной точке пространства.

4. В чем заключается принцип суперпозиции электрических полей?

5. Дайте определение эквипотенциальным поверхностям.

6. Дайте определение дипольному и квадрупольному электрическим моментам.

Литература.

Савельев И.В. Курс общей физики. Кн.3, -М.6: Астрель, 2005. -208 с.

Калашников С.Г. Электричество. М., «Наука», 1978. гл.2, 3.

Сивухин Д.В. Общий курс физики. Т. 3. Электричество. –М.: Физматлит. 2006. -656 с.

Кондратьев А.С., Лаптев В.В. Физика и компьютер. Л., изд. ЛГУ, 1989.

13