Поляризація світла. Основні формули

1. Закон Брюстера

tg і = n_2,1 ,

де і - кут падіння променя; n_2,1 - відносний показник заломлювання.

Рис.16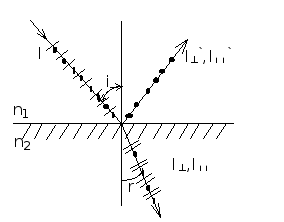

2. Коефіцієнт відбивання падаючого променя:

,

де I_^{`</sup> = ,або I<sub></sub> <sup>`}= ;

I₀ - інтенсивність природного променя.

3. Коефіцієнт заломлювання променя:

,

де I_ - інтенсивність променя з перпендикулярною орієнтацією вектора ;

I_ - інтенсивність променя з паралельною орієнтацією вектора .

4. Ступінь поляризації заломленого променя

.

5. Закон Малюса

I = I₀ cos²  ,

де I - інтенсивність поляризованого світла після аналізатора;

I₀ - інтенсивність світла до аналізатора;

 - кут між площиною поляризатора і площиною поляризації аналізатора.

6. Ступінь поляризації частково поляризованого світла в довільному випадку :

,

де I_max i I_min - максимальна і мінімальна інтенсивності частково поляризованого світла, яке пропускається через аналізатор.

7. Різниця фаз поляризованих променів, яка створюється анізотропною пластинкою

,

де - хвильове число;

l - товщина анізотропної пластинки;

n₃ i n_н - показники заломлювання відповідно звичайного і незвичайного променів в анізотропній пластинці;

8. Кут повертання площини поляризації монохроматичного світла при проходженні через оптично активну речовину:

а) в твердих тілах

 = [] l ;

в) в розчинах

 = [] С l ,

де [] - питоме повертання площини поляризації;

C - масова концентрація оптично активної речовини в розчині;

l - довжина шляху, пройденого світлом в оптично активній речовині.

9. Виникнення оптичної різниці фаз в деяких штучно анізотропних речовинах:

а) у випадку механічних деформацій

,

де - хвильове число;

l - довжина тіла в напрямку створення механічних деформацій;

k₁ - стала величина, характеризує властивості певної речовини;

 - нормальна напруга ( = ).

б) у випадку дії електричного поля (ефект Керра)

,

де k₂ - стала величина;

E - напруженість електричного поля в комірці Керра.

в) у випадку дії магнітного поля

,

де k₃ - стала величина;

Н - напруженість магнітного поля.

Приклади розв’язування задач

Приклад 1. Алмазна призма (n = 2,43) знаходиться в деякому середовищі з показником заломлювання n₁ . Промінь природного світла падає на призму так, як це показано на рис.17. Визначити показник заломлювання цього середовища, якщо відбитий промінь повністю поляризований.

Дано:

n = 2.42

 = 60

--------------------

n₁ - ?

Рис.17

Розв’язування: З рис.17 видно, що кут падіння променя на поверхню алмазної призми  = - 30 = 60.

Для кута  виконується закон Брюстера

tg  = ,

де n - показник заломлювання алмазної призми; n₁ - показник зало- млювання деякого середовища.

Звідки

.

Підставимо числові значення

.

Відповідь: n₁ = 1,40.

Приклад 2. У скільки разів послаблюється інтенсивність світла, яке проходить через систему двох призм Ніколя, площини пропускання яких утворюють кут = 30, якщо відомо, що в кожній із призм втрачається на поглинання 10% падаючої інтенсивності?

Дано:

 = 30

 = 0,1

---------------------

- ?

Розв’язування: Природний промінь, щo падає на грань призми Ніколя, (рис.18) роздвоюється внаслідок подвійного променезаломлювання на звичайний і незвичайний промені. Обидва промені однакові за інтенсивністю і є повністю поляризованими. Звичайний промінь внаслідок повного внутрішнього відбивання на межі шару канадського бальзаму поглинається пофарбованою в чорний колір поверхнею призми. Незвичайний промінь проходить через призму, зменшивши свою інтенсивність на 10% внаслідок відбивання і поглинання в призмі.

Таким чином, інтенсивність світла, яке пройшло першу призму, дорівнює

I₁ = .

Плоскополяризований промінь світла з інтенсивністю І₁ падає на другу призму, де також роздвоюється на звичайний і незвичайний промені. Інтенсивність незвичайного променя І₂ , який пройде крізь другу призму Ніколя, визначається законом Малюса. Врахувавши також втрати інтенсивності на відбивання і поглинання, маємо:

I₂ = I₁ (1 - ) cos²  .

де  - кут між площинами поляризації поляризатора і аналізатора.

Iнтенсивність І₂ з ураxуванням І₁ буде дорівнювати

I₂ = I₀ (1 - )² cos²  .

Послаблення інтенсивності

.

Підставимо числові значення

Відповідь: І₀/I₂ = 3,28 рази.

Приклад 3. На шляху частково поляризованого світла, ступінь поляризації якого 0,6, поставили аналізатор так, що інтенсивність пропущеного ним світла виявилась найбільшою. У скільки разів зменшиться інтенсивність світла, якщо аналізатор повернути на кут 30 ?

Дано:

р = 0,6

 = 30

--------------------

- ?

Розв’язування: Ступінь поляризації для частково поляризованого світла визначається за формулою

 = ,

де І_max і І_min - максимальна і мінімальна інтенсивності частково поляризованого світла, яке пропускається аналізатором.

З цієї формули знайдемо залежність І_max від І_min

. (1)

Максимальна інтенсивність світла, що проходить крізь аналізатор, дорівнює

, (2)

де І_н - інтенсивність поляризованого світла;

І_н.п.- інтенсивність неполяризованого світла.

Мінімальна інтенсивність світла, яке проходить крізь аналізатор, дорівнює

. (3)

Після підстановки (2) і (3) в (1) маємо

.

Звідки

І_n = 1,5І_н.п. (5).

Згідно з умовою задачі аналізатор пропускає в першому випадку

I₁ = I_n + I_н.п.. (6)

В другому випадку

I₂ = I_n cos²  + I_н.п. (7)

Поділивши (6) на (7) та врахувавши (5), одержимо

.

Врахувавши кут , будемо мати

.

Відповідь: І₁/І₂ = 1,23 рази.

Приклад 4. Кут повороту площини поляризації жовтого світла натрію при проходженні через трубку з розчином цукру  = 40 . Довжина трубки l = 15 см. Питоме повертання площини поляризації розчином цукру [] = 0,665 градм²/кг. Визначити концентрацію С цукру в розчині.

Дано:

 = 40

l = 15 см

[  ] = 0,665 градм² /кг.

-------------------------------------

С - ?

Розв’язування: Поворот площини поляризації монохроматичного світла при проходженні його крізь розчин оптично активної речовини (цукру) визначається формулою:

 = [] C l ,

де [] - питоме повертання площини поляризації;

С - масова концентрація оптично активної речовини;

l - хід поляризованого променя в цьому розчині.

Звідки

.

Підставимо числові значення

= 401 (кг/м³).

Відповідь: С = 401 кг/м³.