2. Додавання взаємно перпендикулярних коливань. Фігури Ліссажу

Нехай матеріальна точка Содночасно бере участь у двох гармонічних коливаннях з однаковою циклічною частотою у взаємо перпендикулярних напрямках (рис. 4).

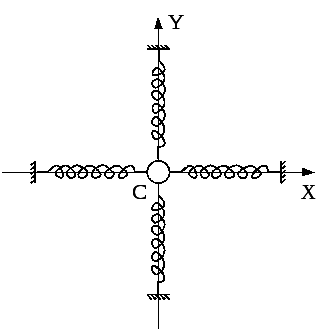
Рис.4

При збудженні коливань матеріальна точка Сбуде рухатись по деякій криволінійній траєкторії, форма якої залежить від різниці фаз обох коливань.

Рівняння коливань точки в напрямках осі xі осіyматимуть вигляд

(23)

де – спільна різниця фаз цих коливань.

Щоб отримати рівняння траєкторії у звичайному вигляді, треба виключити з цих рівнянь час t.

В результаті отримаємо

(24)

Рівняння (24) є рівнянням траєкторії результуючого коливання точки С.Це рівняння є еліпсом, осі якого повернуті відносно осейxіy.Орієнтація еліпса і величина його півосей залежить від амплітудіі різниці фаз.

Розглянемо окремі випадки.

1. Нехай , деТоді

звідки

(25)

Результуюче коливання є гармонічним коливанням вздовж прямої з частотою ωі амплітудою(рис.5).

Рис.5

Пряма утворює з віссю xкут

2. Нехай де

У цьому випадку

звідки

(26)

Результуючий рух – це гармонічне коливання вздовж прямої (рис.6).

3. Нехай деВ результаті одержуємо рівняння

(27)

Це рівняння еліпса, осі якого збігаються з осями координат, а його півосі дорівнюють відповідним амплітудам (рис. 7). Якщо , то еліпс перетворюється в коло.

Рис.6

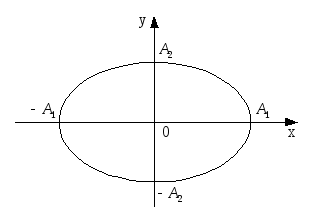
Рис.7

Два окремі випадки івідрізняються напрямком коливання по еліпсу або по колу. У випадку, коли циклічні частоти взаємно перпендикулярних коливань, що додаються, різні, то замкнута траєкторія результуючого коливання досить складна.

Замкнуті траєкторії, які рисуються одночасно коливальною точкою у взаємно перпендикулярних напрямках, називаються фігурами Ліссажу. Форма цих кривих залежить від співвідношення амплітуд, частот і різниці фаз коливань, які додаються.

На рис. 8 показана одна із найпростіших траєкторій, одержаних при додаванні взаємно перпендикулярних коливань з відношенням циклічних частот 1:2 і різниці фаз . Рівняння коливань мають вигляд:

,. (28)

Рис. 8

Якщо відношення частот дорівнює 1:2, а різниця фаз, то траєкторія коливань точки вироджується в незамкнуту криву (рис. 9), вздовж якої рухається точка то в одну то в протилежну сторони.

Рис. 9

Чим ближче до одиниці буде відношення частот , тим складнішою буде фігура Ліссажу. Для прикладу на рис. 10 наведена крива фігури Ліссажу з відношенням частот 3:4 і різницею фаз.

Рис. 10

3. Диференціальне рівняння вільних згасаючих коливань і його розв’язування

Розглянемо вільні згасаючі коливання, амплітуда яких внаслідок втрат енергії реальною коливальною системою зменшується з часом. Найпростішим механізмом зменшення енергії коливань є її перетворення в теплоту внаслідок тертя в механічних коливальних системах, а також омічних втрат і випромінювання електромагнітної енергії в електричних коливальних системах.

Закон згасання коливань визначається властивостями коливальних систем. Як правило розглядають лінійні системи – ідеалізовані реальні системи, у яких параметри, які визначають фізичні властивості системи, у ході процесу не змінюються. Лінійними системами є, наприклад, пружинний маятник при малих деформаціях пружини (в межах дії закону Гука), коливальний контур, індуктивність, ємність і опір якого не залежать ні від струму в контурі, ні від напруги. Різні за своєю природою лінійні системи описуються ідентичними лінійними диференціальними рівняннями, які дозволяють підходити до вивчення коливань різної фізичної природи з єдиної точки зору.

Диференціальне рівняння вільних згасаючих коливань лінійної системи задається у вигляді

(29)

де x – коливна величина, яка описує той або інший фізичний процес;

– коефіцієнт згасання;

ω₀ – циклічна частота вільних незгасаючих коливань цієї ж коливальної системи, тобто при (при відсутності втрат енергії).

Щоб знайти розв’язок рівняння (29), слід фізичну величину х виразити через нову змінну z відповідно до рівняння

(30)

де z = z (t).

Після підстановки першої і другої похідних від рівності (30) в рівняння (29) одержимо

(31)

Розв’язок рівняння (31) залежить від знака коефіцієнта перед шуканоювеличиною. Розглянемо випадок, коли цей коефіцієнт додатний, тобто _.

Тоді одержимо рівняння типу

(32)

де

. (33)

Розв’язком рівняння (32) є рівняння типу (9) першої теми:

(34)

Після підстановки (34) у (30) для випадку малих загасань _{одержуємо розв’язок рівняння (29) у такому вигляді:}

(35)

де ─ амплітуда згасаючих коливань;

А_о – початкова амплітуда.

Залежність (35) показана на рис. 11 суцільною лінією, а амплітуда коливань – пунктирними лініями.

Проміжок часу , протягом якого амплітуда згасання коли- вань зменшується у е разів, називається часом релаксації.

Згасання порушує періодичність коливань, тому згасаючі коливання не є періодичними, і до них поняття періоду або частоти незастосовне.

Однак якщо згасання малі, то можна умовно користуватися поняттям періоду як проміжку часу між двома послідовними максимумами (або мінімумами) коливань тієї чи іншої фізичної величини (рис. 11).

Період згасаючих коливань з урахуванням формули (33) дорівнює

(36)

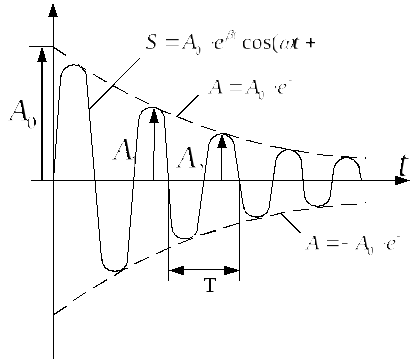
Рис. 11

Якщо Α (t) і Α (t + T) – амплітуди двох послідовних коливань, які відповідають моментам часу, що відрізняються на один період, то їх відношення

,

називається декрементом згасання, а його логарифм

(37)

називається логарифмічним декрементом згасання, а величина N визначає число коливань, які виконує коливальна система за час зменшення амплітуди в е разів.

Для характеристики втрат енергії коливальною системою з часом, користуються поняттям добротності , яка при малих значеннях логарифмічного декремента є помноженим на 2відношенням повної накопленої системою енергії до середніх втрат енергії цією системою за час в один період, тобто

(38)

де W ─ повна енергія системи;

ΔW(T) ─ середні втрати енергії системою за час в один період (t=T).

Повна енергія коливальної системи в момент часу t дорівнює

(39)

Енергія коливальної системи через час в один період дорівнює

(40)

Втрати енергії системою за час в один період легко знайти відніманням від співвідношення (39) співвідношення (40), тобто

(41)

Добротність коливальної системи одержимо, якщо поділити (39) на (41) і помножити одержану величину на 2

(42)

де δ – логарифмічний декремент згасання.

У виразі (42) враховано, що відношення

У випадку, коли , то в формулі (42) період коливаньT приймають рівним T₀.