
Fizika_lektsiyi
.pdf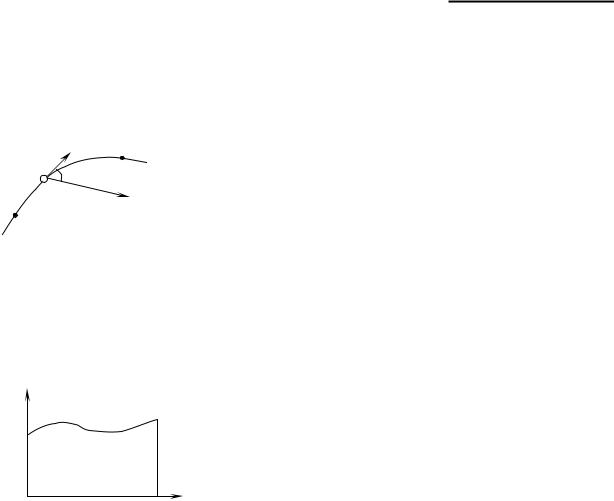
Лекція 5
ЗАКОН ЗБЕРЕЖЕННЯ МЕХАНІЧНОЇ ЕНЕРГІЇ
1 Механічна робота. Потужність
Нехай частка під дією сили F рухається по деякій траєкторії
із точки 1 у точку 2 (Рис. 5.1). У загальному випадку сила F може змінюватися як по величині, так і по напрямку. Розглянемо елемен-
тарне переміщення d r , у межах якого силу F можна вважати постійною. Елементарною роботою dA сили F по переміщенню
R
d r називають величину, рівну скалярному добутку (F dr ) :
|
|
R |
|
dA = F cosα dr = Fs ds . |
|
|||
dA = (F × dr ) , |
або |
(5.1) |
||||||
де Fs |
= F cosα - проекція сили F на напрямок руху, |
ds =| dr | . |
||||||
Fs |
|
Робота dA - величина алгебраїчна. Якщо кут |
||||||
2 |
α < π , то робота додатна, якщо α > π , то робо- |
|||||||
α |
|
|||||||
|
|
|
2 |
|
π |
2 |
|
|
1 |
|
|
|
|
|
|
||
F |
та від’ємна. |
При α = робота тотожно дорів- |
||||||
|
||||||||
Рисунок 5.1 |
нює нулю. |
|
2 |
|
|
|||
Робота |
вимірюється в |
Джоулях |
||||||
|
|
(Дж). Розмірність |
Джоуля дорівнює |
добутку |
||||
розмірності сили (Н) на розмірність переміщення: Дж=Н м. Робота, здійснююча на кінцевому шляху s дорівнює сумі елементарних робіт на окремих ділянках ds або інтегралу
Fs |
s |
|
|
A = ∫ Fs ds . |
(5.2) |
||
|
|||
|
0 |
|
|
А |
Роботі можна надати наочний геомет- |
||
s |
ричний зміст. Якщо сила Fs задана як |
||
функція пройденого шляху s, то робота на |
|||
Рисунок 5.2 |
цьому шляху виміряється площею обмеже- |
||
|
|||
|
ною кривою Fs (s) в координатах s |
й Fs |
|
(Рис. 5.2). Якщо на частку одночасно діють кілька сил, то робота результуючої сили дорівнює алгебраїчній сумі робіт, здійснюючих кожною із сил на тім же переміщенні:
R R |
R |
R |
R |
R R |
R R |
+ ... = A1 |
+ A2 |
+ ... |
A = ∫ F d r |
=∫(F1 |
+ F2 |
+ ...) d r |
= ∫ F1 dr |
+ ∫ F2dr |
33

Величина, що характеризує швидкість виконання роботи си-
лою F , і рівна роботі, виконаній в одиницю часу, називається потужністю:
|
dA |
|
R |
R R |
|
|||
|
|
Fdr |
|
|||||
N = |
|
|
= |
|
|
= F v . |
(5.3) |
|
d t |
d t |
|||||||
|
|
|
|
|||||
Величина потужності в системі СІ вимірюється в Ваттах (Вт), і Вт=Дж/с. Ми також знаємо ще одну одиницю виміру потужності - кінська сила: 1к.с. = 736 Вт.
2 Кінетична енергія. Теорема про кінетичну енергію
Розпишемо вираз для роботи (5.1), скориставшись другим законом Ньютона:
R R |
|
R |
|
|
mv2 |
|
|||
|
d v |
R |
R R |
|
|
||||
dA = F d r |
= m |
|
d r |
= m vd v |
= d ( |
|
) . |
(5.4) |
|
dt |
2 |
||||||||
|
|
|
|
|
|
|
|||
Фізична величина рівна:
T = |
mv2 |
, |
(5.5) |
|
|||
2 |
|
|
|
називається кінетичною енергією. Відзначимо, що в різних інерціальних системах відліку швидкість тіла може бути різною. Отже, кінетична енергія залежить від вибору інерціальної системи відліку. Тут же відзначимо, що кінетична енергія - величина ади-
тивна. З формули (5.4) випливає, що елементарна робота рівнодіючої всіх сил дорівнює повному диференціалу від кінетич-
ної енергії. Якщо в результаті дії сили F швидкість тіла змінилася від v1 до v2, то, інтегруючи (5.4), отримуємо
v |
m v |
2 |
|
m v2 |
2 |
2 |
|
|
|
2 |
|
|
|
||||||
A = ∫d ( |
|
) = |
|
− |
m v1 |
= T2 − T1 . |
(5.6) |
||
2 |
|
|
|
|
|||||
v |
2 |
|
2 |
|
|
||||
1 |
|
|
|
|
|
|
|
|
|
Або, збільшення кінетичної енергії частки на деякому пе-
реміщенні дорівнює алгебраїчній сумі робіт всіх сил, під дією яких відбувалося це переміщення. Формулу (5.6) називають теоре-
мою про кінетичну енергію6.
6 Підкреслимо ще раз, що в цій теоремі мова йде про роботу саме рівнодіючої всіх сил, що діють на тіло, так як при виведенні формули (5.5) ми скористалися другим законом Ньютона.
34
З формули (5.4) випливає, що кінетична енергія виміряється, як і механічна робота, у Джоулях.
Тепер розглянемо тіло маси m, що обертається з кутовою швидкістю ω навколо нерухомої осі. Кінетичну енергію знайдемо, просумувавши кінетичні енергії малих часток маси mі, на які
розіб'ємо тіло |
|
|
|
|
|
|
|
|
|
|
T = ∑ |
mi vi2 |
= ∑ |
mi ω2 ρi2 |
= ω 2 |
∑mi |
ρi2 = |
Jω 2 |
. |
||
2 |
2 |
|
|
|||||||
i |
i |
|
2 |
i |
2 |
|
||||
Тут ρi - відстань від і - ої частки до осі обертання. Таким чи- |
||||||||||
ном, кінетична енергія тіла, що обертається |
|
|
|
|
||||||
|
|
T = |
Jω 2 |
. |
|
|
(5.7) |
|||
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
І знову відзначимо схожість формул для поступального й обертального рухів - на цей раз кінетичних енергій поступального (5.5) і обертального рухів (5.7).
Тепер можна легко знайти вираз для роботи рівнодіючої всіх сил при обертанні тіла навколо нерухомої осі. На підставі теореми про кінетичну енергію (5.6) маємо
|
Jω |
2 |
|
|
dA = dT = d |
|
|
= J ω dω = Jωε dt = Jε dϕ = Mdϕ . (5.8) |
|
2 |
|
|||
|
|
|
|
|
Тут ми скористалися основним законом динаміки обертального руху (4.9) M=J ε, а також врахували, що dω = ε d t . З формули (5.8) випливає, що при обертальному русі робота виконується моментом сил.
У випадку плоского складного руху кінетична енергія тіла буде складатися із двох частин - кінетичної енергії поступального руху його центра мас і кінетичної енергії обертання навколо центра
мас із кутовою швидкістю ω |
|
|
Jω2 |
|
||
|
mv2 |
|
||||
T = |
c |
+ |
c |
. |
(5.12) |
|
2 |
2 |
|||||
|
|
|
|
|||
3Консервативні сили. Потенціальна енергія.
Усучасному природознавстві прийнято вважати, що взаємодія тіл здійснюється за допомогою полів. Полем сил називають область простору, у кожній точці якої на частку діє сила, що закономірно змінюється від точки до точки. Інакше кажучи, якщо в кожній точці
35
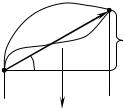
2 |
простору на матеріальну точку діють сили, то |
|||
r |
говорять, що в просторі визначене силове по- |
|||
h |
ле. Приклад силового поля - поле сили тяжін- |
|||
1 α |
ня. Нехай тіло переміщається із точки 1 у точ- |
|||
m g |
ку 2 (Рис. 5.3). Обчислимо роботу, що |
|||
Рисунок 5.3 |
здійснює сила ваги при цьому переміщенні. |
|||
Відповідно до визначення механічної роботи |
||||
|
||||
(5.1) ми можемо записати |
|
|
||
|
2 |
R R |
|
|
|
|
|
||
|
A = ∫ mg dr . |
(5.13) |
||
1
Тепер скористаємося обставиною, що поблизу поверхні Землі сила ваги постійна: mg = const . Постійну величину можна винести з під знака інтеграла й вираз (5.13) для роботи запишеться так –
R 2 R |
|
A = mg ∫dr . |
(5.14) |
1
Інтеграл у виразі (5.14) являє собою суму елементарних переміщень dr , які робить тіло при своєму русі із точки 1 у точку 2. Очевидно, що сума всіх елементарних переміщень буде дорівнювати r . Отже, вираз (5.14) приймає вид
R |
R |
= mg | |
R |
π |
R |
A = mg |
r |
r |
| cos( |
+ α ) = −mg | r | sin α = |
|
|
|
|
|
2 |
(5.15) |
= −mg h = −mg (h2 − h1 ),
де h1 - висота, на якій перебуває тіло над поверхнею Землі в початковому положенні 1, і h2 - висота в кінцевому положенні 2. А тепер саме головне. При обчисленні роботи сили ваги ми нічого не говорили, про траєкторію, по якій рухається наше тіло. Очевидно, що для будь-якої траєкторії, що веде із точки 1 у точку 2, вектор переміщення r буде тим самим , і, згідно (5.15), для всіх траєкторій робота сили ваги буде мати також те саме значення. Тобто , робота сили ваги не залежить від форми траєкторії, а визначаться тільки початковою й кінцевою висотою тіла над поверхнею Землі.
Сили, робота яких не залежить від форми траєкторії, за якою частка переходить із одного положення в інше, а визначається тільки початковим і кінцевим положенням частки, на-
36

зиваються консервативними.7 У цьому випадку кожному поло-
женню частки в силовому полі можна зіставити деяку функцію U (r ) таку, що різниця значень цієї функції в точках 1 й 2 визначає роботу сил поля по переміщенню частки між цими точками
A12 = U1 - U2 . |
(5.16) |
Функцію U називають потенціальною енергією частки. Порівнюючи формули (5.15 - 5.16), ми дійдемо до висновку, що потенціальна енергія тіла в полі сили ваги описується формулою
U = mgh , |
(5.17) |
де h - висота, на якій перебуває тіло над поверхнею Землі.
До консервативних сил відносяться й сили пружності. Знайдемо потенціальну енергію пружної деформації. Сила пружності (див. лекцію 2, формула (2.10)) дорівнює
F = -kx . |
(5.18) |
Тут х - зсув кінця пружини з положення рівноваги. Якщо ми будемо розтягувати або стискати пружину, то, на підставі 3-го закону Ньютона, робота зовнішньої сили, протилежно спрямованій силі пружності пружини, буде дорівнювати
x |
x |
kx |
2 |
|
|
|
A = ∫ Fdx = ∫ kxdx = |
. |
(5.19) |
||||
2 |
|
|||||
0 |
0 |
|
|
|
||
|
|
|
|
|||
Ця робота зовнішньої сили була витрачена на збільшення потенціальної енергії пружини. Якщо вважати, що енергія пружини в недеформованому стані дорівнює 0, то тоді
U = |
kx2 |
. |
(5.20) |
|
|||
2 |
|
|
|
Потенціальну енергію часто називають енергією взаємодії. Дійсно, у першому прикладі взаємодіють тіло й Земля, у випадку пружини взаємодіють окремі частини одного тіла (нагадаємо, що сили пружності з'являються при зміні взаємного положення заряджених часток, з яких складається тіло).
Ще один приклад консервативних сил - центральні сили. Так називають сили, величина яких залежить тільки від відстані між двома частками, а спрямовані вони уздовж лінії, що з’ єднує ці
7 Інша назва цих сил - потенціальні. Ми будемо використовувати ці терміни як синоніми.
37
частки (Рис. 5.4). Центральними є сила Всесвітнього тяжіння й сила Кулона (2.5, 2.6). З рисунка 5.4 видно, що для центральних сил еле-
R
ментарна робота Fd r буде дорівнювати
R |
= F (r)dr . |
dA = F (r)d r |
Відповідно, робота, здійснена на кінцевому шляху s дорівнює
R R |
r2 |
|
A = ∫ Fdr |
= ∫ F ( r)dr . |
(5.21) |
|
r1 |
|
З (5.21) ясно, що повна робота залежить від початкової й кінцевої відстаней від частки до силового центра, і не залежить від форми траєкторії. Підставимо у формулу (5.21) вираз для сили Всесвітнього тяжіння (2.5)
r2 |
R R |
r2 |
Mm |
|
1 |
|
1 |
|
|
1 |
|
1 |
|
|
A12 = ∫ Fdr |
= −∫ G |
dr = GMm |
− |
|
= −GMm |
− |
. (5.22) |
|||||||
2 |
|
|
|
|
||||||||||
r |
|
r |
r |
r2 |
|
r1 |
r1 |
|
r2 |
|||||
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Знак "-" перед інтегралом відображує той факт, що напрямки сили й переміщення протилежні, якщо початок координат поміщений на силовому центрі. З (5.22) і (5.16) можна зробити висновок, що потенціальна енергія сил тяжіння дорівнює
U (r ) = − |
GMm |
. |
(5.23) |
|
|||
|
r |
|
|
І ще кілька слів про потенціальну енергію. Згідно (5.16), робота консервативної сили буде дорівнювати зменшенню потенціальної енергії
R |
(5.24) |
Fd r = −dU . |
|
Розписуючи скалярний добуток, одержимо |
|
Fx dx + Fy dy + Fz dz = − dU . |
(5.25) |
Якщо переміщення частки відбувалося тільки уздовж x, у той |
|
час як y й z координати залишалися постійними, то F = − |
∂U . Тут |
x |
∂ x |
|
|
значок ∂ означає часткову похідну за координатою, що береться, коли інші координати залишаються незмінними. Аналогічним образом одержимо компоненти сил Fy й Fz. Таким чином
38

F = − |
∂U , |
F = − |
∂U , |
F = − |
∂U . |
(5.26) |
x |
∂ x |
y |
∂ y |
z |
∂z |
|
|
|
|
|
Відповідно до (5.26) ми маємо 3 проекції сили на осі координат. Якщо помножимо їх на відповідні одиничні вектори й складемо, то одержимо вектор сили
R |
|
∂U |
R |
∂U |
R |
∂U |
R |
(5.27) |
F = - |
¶x |
i - |
¶y |
j - |
¶ z |
k , |
||
|
|
|
|
|
|
|||
або, у скороченому вигляді |
|
|
|
|
|
|||
|
F = -gradU . |
|
|
(5.28) |
||||
Тут мається на увазі, що |
|
|
|
|
|
|
||
gradU = |
∂U R |
∂U |
R |
∂U |
R |
|||
¶ x |
i + |
¶y |
j + |
¶ z |
k . |
|||
|
|
|
|
|
|
|||
Відповідно до (5.28) grad U є вектором (читається "градієнт U"), хоча функція U є скаляром. Поряд з (5.28) використовується позначення ÑU: gradU º ÑU , де Ñ (набла) - диференціальний оператор, також називається оператором Гамільтона, є
Ñ = |
|
∂ |
R |
+ |
|
∂ |
R |
+ |
∂ |
R |
||
|
|
i |
|
|
j |
|
|
k . |
||||
¶ x |
¶ y |
¶ z |
||||||||||
|
|
|
|
|
|
|||||||
Відзначимо, що grad якої-небудь скалярної функції, як це доводиться у вищій математиці, визначає напрямок найбільш швидкого росту цієї функції. Якщо ця властивість градієнта скалярної функції застосувати до потенціальної енергії, то з рівняння (5.28)
виходить, що консервативні сили завжди спрямовані убік найбільш швидкого зменшення потенціальної енергії.8
4 Закон збереження механічної енергії
Нехай на частку діють тільки консервативні сили. Тоді, з однієї сторони, робота за переміщенням частки із точки 1 у точку 2 визначається виразом (5.16): A12=U1 -U2, а з іншого боку, ця робота визначає зміну кінетичної енергії (5.6): A12=T1 -T2. Отже,
T2 - T1= U1 - U2 або T1 + U1 = T2 + U2. |
(5.28) |
8 Ілюстрацією цього твердження є положення русла рік. Вони завжди перебувають у місцях з найменшою для даної місцевості потенціальною енергією поля сили ваги.
39

Таким чином, ми одержали, що величина E=T+U, для частки, що перебуває в полі дії консервативних сил, залишається постійної
E = T+U = const. |
(5.29) |
Фізична величина Е, рівна сумі кінетичної і потенціальної
енергій частки, називається повною механічною енергією част-
ки. Відповідно до (5.16) можна сказати, що робота відбувається за рахунок зменшення потенціальної енергії частки в полі консервативних сил, при цьому ця робота, згідно (5.6), іде на збільшення кінетичної енергії частки dT = - dU.
Нехай, крім потенціальних сил, що результуюча якої дорівнює F, на частку діє також і неконсервативна сила F*. Тоді, при переході частки з положення 1 у положення 2 на неї буде здійснюватися робота
A12 = ∫ Fds + ∫ F * ds = Aконс + A *.
Відповідно до теореми про збільшення кінетичної енергії A12=dT і, таким чином
T2 − T1 = U1 − U2 + A *,
або
E2 - E1 = A*. |
(5.30) |
Таким чином, ми одержали, що робота неконсервативних сил затрачується на збільшення повної механічної енергії частки.
Розглянемо тепер систему часток (тіл), між якими діють консервативні сили та ця система перебуває в зовнішнім силовому полі консервативних сил9 , і, крім того, нехай на частки системи діють неконсервативні сили. Тоді, як ми вже знаємо, збільшення кінетичної енергії кожної частки дорівнює алгебраїчній сумі робіт, які здійснюють всі сили
dT = ( d Aпот + d Aпот |
+ d A*) |
, |
(5.31) |
||
i |
вз |
внешн |
i |
|
|
де індекс і означає номер частки. З урахуванням того, що роботу потенціальних сил можна представити як зміну потенціальної енергії частки у відповідному силовому полі
dAпот = −dU |
вз |
, |
d Aпот |
= −dU |
внешн |
. |
вз |
|
внешн |
|
|
9 Наприклад, електрично заряджені тіла, які перебувають у зовнішнім електричному полі.
40
вираз (5.31) можна переписати у вигляді
(dT + dU |
вз |
+ dU |
внешн |
) |
i |
= dA* . |
(5.32) |
|
|
|
i |
|
Введемо поняття повної механічної енергії системи, як суми кінетичної і потенціальної енергій всіх часток системи
E = ∑( T + Uвз + Uвнешн )i .
i
Тепер, підсумовуючи вираз (5.32) по всіх частках розглянутої системи, одержимо
dE = ∑ dAi* . |
(5.33) |
i |
|
Тобто, як і для однієї частки (5.30), повна механічна енергія системи часток змінюється за рахунок роботи тільки неконсервативних сил, які діють на окремі частки системи. Якщо неконсервативні сили відсутні, то з (5.33) одержуємо
E = ∑(T + Uвз + Uвнешн ) = const . |
(5.34) |
i |
|
Отже, повна механічна енергія системи тіл, на які діють тільки консервативні сили, залишається постійною. Це і є закон збереження повної механічної енергії.
У теоретичній фізиці доводиться, що закон збереження механічної енергії є наслідком однорідності часу. Однорідність часу означає незалежність фізичних законів від початку відліку часу, тобто говорить про рівнозначність всіх моментів часу.
Особливий випадок неконсервативних сил представляють сили тертя. Робота сил тертя завжди негативна, тому що сили тертя спрямовані проти вектора швидкості
R |
R |
dAтр = Fтрdr |
= Fтрvdt = −Fтрv dt < 0 . |
Відповідно до рівняння (5.33) повна механічна енергія системи при наявності тертя зменшується. Такий процес називається дисипацією, або розсіюванням енергії, а сили, які приводять до втрати механічної енергії, називаються дисипативними. Крім розглянутої нами повної механічної енергії в природі існують інші види енергії. Як Ви знаєте з повсякденного досвіду, при терті тіла нагріваються, а це значить, що повна механічна енергія переходить
41
у внутрішню енергію ("теплову" енергію) взаємодіючих тіл. У цьому смислі рівняння
E = A*
також є законом збереження енергії, якщо відомо, у які форми переходить механічна енергія системи. Для енергії, як єдиної характеристики різних форм руху матерії справедливий закон збереження енергії, що може бути сформульований таким чином: енергія
ніколи не зменшується й не збільшується, не зникає й не з'яв-
ляється знову, вона лише перетворюється з одного виду в інший.
Але це вже питання іншого розділу фізики - термодинаміки, який ми будемо вивчати пізніше.
5 Потенціальна яма. Умови рівноваги механічної системи
Нехай на частку діють тільки консервативні сили. Як ми вже знаємо, у цьому випадку повна механічна енергія частки зберігається
E = T + U = const.
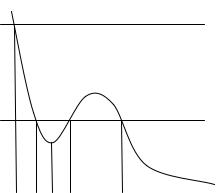
Оскільки кінетична енергія за своїм визначенням завжди додатна, то це значить, що повна механічна енергія не може бути меншою, чим потенціальна
|
|
|
|
|
|
|
E ³U. |
|
|
(5.35) |
U |
|
A |
|
|
|
|
Так як потенціальна енергія за- |
|||
|
|
|
|
|||||||
|
|
|
|
|
лежить тільки від координат частки, |
|||||
|
|
|
|
|
|
|||||
Е2 |
|
|
|
|
|
|
то відношення |
(5.35) |
визначає об- |
|
|
|
|
|
|
|
ласть простору, |
у межах якої може |
|||
|
|
|
|
n |
|
|
||||
|
|
|
|
|
|
перебувати |
частка |
із заданою |
||
|
|
|
B C |
D |
|
|||||
Е1 |
|
|
|
енергією Е. Частка не може проник- |
||||||
|
|
m |
|
|
|
|||||
|
|
|
|
|
|
нути в область, де U>E, оскільки по- |
||||
|
|
I |
II |
III |
IV |
|
||||
|
|
|
тенціальна |
енергія не |
може бути |
|||||
|
|
|
x0 |
|
|
|
більше повної енергії. |
|
||
0 xA |
xB |
xC |
xD |
|
|
|||||
x |
|
|
|
|||||||
Як приклад розглянемо частку, Рисунок 5.5 здатну здійснювати тільки одномір-
ний рух, наприклад, уздовж осі Ох. Тоді залежність потенціальної енергії від координат зведеться до залежності від х: U=U(x). І, нехай, ця залежність має вигляд, зображена на рисунку 5.5. Пряма Е1 на цьому рисунку відповідає руху частки з повною енергією
42
