3.5 Потенціальна енергія деформації

Потенціальною енергією деформації називається енергія, яка накопичується в тілі при його пружній деформації. Коли під дією зовнішнього статичного навантаження тіло деформується, точки прикладання зовнішніх сил переміщуються і потенціальна енергія положення вантажу зменшується на величину, яка чисельно дорівнює роботі, виконаній зовнішніми силами. Енергія, витрачена зовнішніми силами, не зникає, а перетворюється, в основному, в потенціальну енергію деформації тіла. Решта, незначна частина розсіюється, головним чином, в вигляді тепла за рахнок різних процесів, що проходять в матеріалі при його деформації.

Величину потенціальної енергії деформації, що припадає на одиницю об'єму тіла, називають питомою потенціальною енергією деформації і визначають за формулою

(3.12)

Маючи на увазі, що , одержимо для питомої потенціальної енергії деформації вираз

(3.13)

Для загального випадку визначення питомої потенціальної енергії деформації при об'ємному напруженому стані, якщо задані головні напруження формула має вигляд

(3.14)

При деформації елемента змінюється, як його об'єм, так і форма (із куба він перетворюється на паралелограм). В зв'язку з цим можна вважати, що повна питома потенційна енергія деформації

(3.15)

де u_V  питома потенціальна енергія зміни об'єму, тобто енергія, яка накопичується за рахунок зміни об'єму;

u_ф  питома потенціальна енергія формозміни, тобто енергія, яка накопичується внаслідок зміни форми елементу.

Безпосередньо визначити u_ф важко, тому спочатку визначимо u_V.

(3.16)

Тепер, згідно формули (3.15),

Підставляючи сюди значення u і u_v із (3.14) і (3.16), після елементарних перетворень отримаємо, що

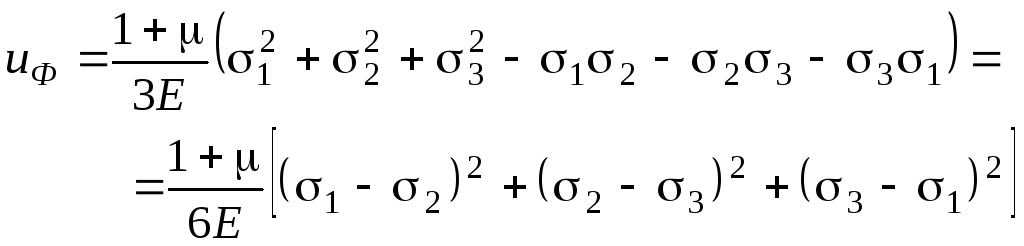(3.17)

Це і є шуканий вираз для питомої потенціальної енергії формозміни.

4 Теорії міцності

4.1 Оцінка міцності при складному напруженому стані

При лінійному напруженому стані, коли діє тільки одне головне напруження (при розтяганні) або (при стисканні), умова міцності записується у вигляді

 ₁  _р або ₃  _с

де _р і _с  допустимі напруження відповідно при розтяганні і при стисканні, які встановлюються залежно від величини граничного напруження для даного матеріалу.

Граничне напруження (границя текучості для пластичних матеріалів або границя міцності для крихких) у цьому випадку легко може бути знайдене експериментально в дослідах на розтягання або стискання.

Значно складніше оцінити міцність при складному напруженому стані. Настання небезпечного стану в цьому випадку залежить не тільки від абсолютних величин головних напружень, а також від їх співвідношень. Для оцінки міцності при складному напруженому стані лабораторним шляхом потрібно виконати дуже багато складних випробувань зразків з метою реалізації різних величин і співвідношень головних напружень, що практично здійснити не можливо.

Щоб можна було судити про міцність при складному напруженому стані, треба знати істинні причини руйнування матеріалу. Ці теорії дають можливість скласти умови міцності при складному напруженому стані, виходячи з даних про міцність матеріалу, одержаних з випробувань на просте розтягання або стискання.

Напружені стани при складному напруженому стані і при одноосному розтяганні називатимемо рівнобезпечними або еквівалентними, якщо при пропорційному збільшенні головних напружень в одне і теж число разів вони одночасно стають граничними. Інакше кажучи, коефіцієнти запасу міцності для еквівалентних напружених станів однакові.

Еквівалентним напруженням називають таке умовне напруження одноосного розтягування, яке рівнобезпечне заданому випадку складного напруженого стану.

Відповідно до гіпотез міцності виводять формули для розрахунку еквівалентного напруження, яке потім порівнюють з допустимим напруженням на розтягання. Таким чином умова міцності матиме вигляд

_екв  _р (4.1)