Лабораторна робота №3

ДОСЛІДЖЕННЯ РОЗПОДІЛУ ТЕМПЕРАТУРИ ПО ДОВЖИНІ

ТЕПЛОПРОВІДНОГО СТЕРЖЯ ТА ВИЗНАЧЕННЯ

ЙОГО СЕРЕДНЬОГО КОЕФІЦІЄНТА ТЕПЛОВІДДАЧІ

Мета роботи: 1) визначити розподіл температури по довжині теплопровідного стержня для стаціонарних процесів теплопровідності і конвективної тепловіддачі; 2)за знайденим експериментально середнім темпом охолодження стержня розрахувати коефіцієнт його тепловіддачі при температурі навколишнього середовища, що має місце при проведені досліджень.

1 Теоретичні відомості

Розглянемо стаціонарний процес теплообміну нагрітого довгого теплопровідного стержня з будь-якою формою поперечного перерізу (рисунок Л3.1) і із защемленим одним кінцем та вільним іншим.

Защемлений кінець має температуру t₀=const. Коефіцієнт тепловіддачі бокової поверхні стержня α_p=const. Коефіцієнт теплопровідності матеріалу стержня λ=const. Геометричні параметри стержня задані його площею поперечного перерізу А та параметром U, температура навколишнього середовища t_р=const і кінця стержня t₁=const.

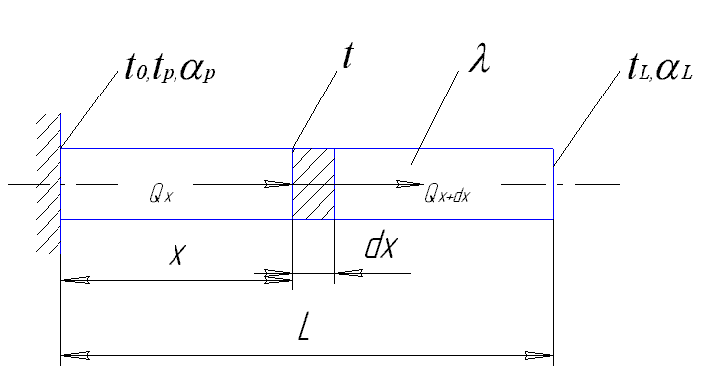
Рисунок Л3.1 – Схема для розрахунку розподілу температури по довжині довгого теплопровідного стержня

Виділимо на відстані х від защемленого кінця стержня елементарну ділянку dx і розглянемо зміну теплового потоку dQ_X, який проходить через поперечний переріз А стержня на відстані dx

:

dQ_X=Q_X -Q_X-dХ, (Л3.1)

де Q_X – тепловий потік, який входить в елемент dx;

Q_X-dХ – тепловий потік, що виходить з елемента dx.

Оскільки за прийнятими умовами процеси теплопровідності і конвективної тепловіддачі стаціонарні, то зручно оперувати не значеннями температури, а температурними напорами:

Δt₀=t₀ – t_p; (Л3.2)

Δt=t – t_p; (Л3.3)

де Δt₀ – температурний напір на защемленому кінці стержня, t₀=const;

Δt – поточний температурний напір, Δt=var;

t – поточна температура стержня, яка при стаціонарному процесі теплопровідності однакова в усьому поперечному перерізі і змінюється тільки по довжині стержня. Зміну температурного напору Δt΄ на ділянці dx можна за відомими правилами математики подати так:

. (Л3.4)

За законом Фур’є теплові потоки:

; (Л3.5)

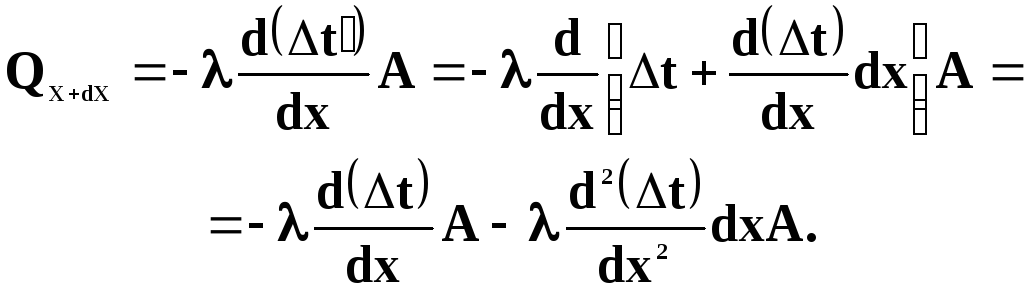(Л3.6)

Підставивши (Л3.5) та (Л3.6) в (Л3.1), знайдемо

. (Л3.7)

Стержень в стаціонарному режимі обмінюється теплотою з навколишнім середовищем, тоді за законом Ньютона – Ріхмана:

. (Л3.8)

Порівнюючи (Л3.7) та (Л3.8), отримаємо однорідне диференціальне рівняння другого порядку, яке описує розподіл температури по довжині стержня

, (Л3.9)

де - темп охолодження стержня.

Загальний розв’язок рівняння (Л3.9) [1,2]:

, (Л3.10)

де С₁ та С₂ – сталі інтегрування.

Оскільки, стержень має скінчену довжину, то умови однозначності розв’язку (Л3.10) можна записати так [2]:

при x=0Δt=Δt₀;

при x=L; (Л3.11)

або ,

де Δt_L– температурний напір на кінці стержня;

α_L– коефіцієнт тепловіддачі з торцевої поверхні стержня.

При x=Lкількість теплоти, що підведена до торця стержня за рахунок теплопровідності, дорівнює кількості теплоти, що віддається поверхнею торця в навколишнє середовище.

Використовуючи умови (Л3.11) та рівняння (Л3.10), знайдемо сталі інтегрування С₁таС₂:

при x=0Δt₁=C₁+C₂;

при x=L (Л3.12)

та ,

звідки: ;.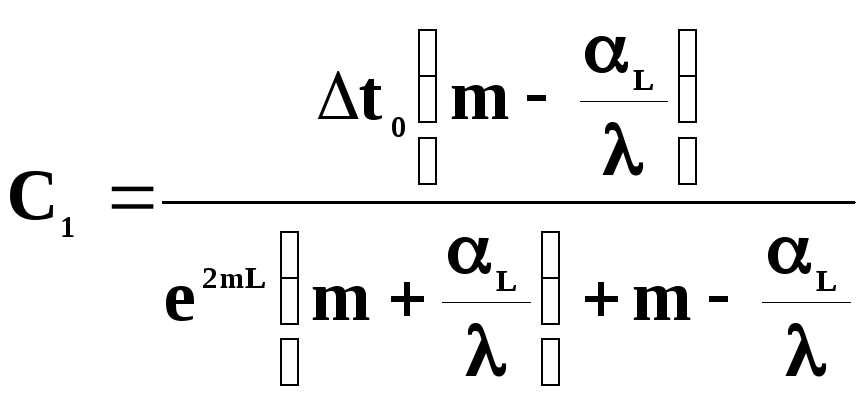

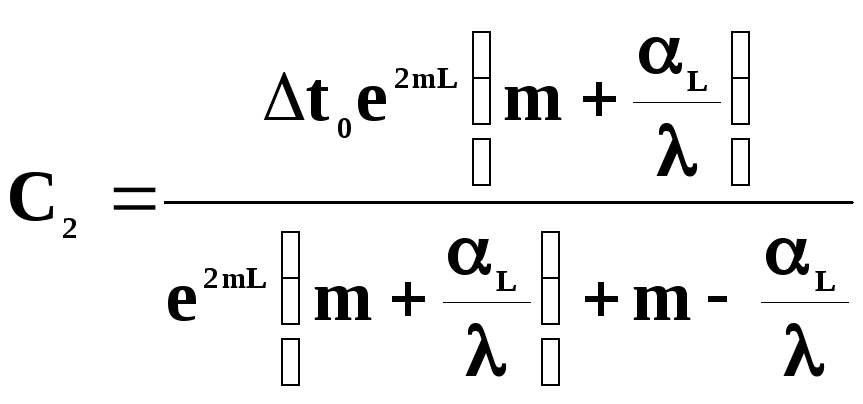Підставляючи С₁та С₂ в (Л3.10), отримуємо після нескладних перетворень, закон зміни температури по довжині стержня скінченої довжини для стаціонарних процесів теплопровідності і тепловіддачі

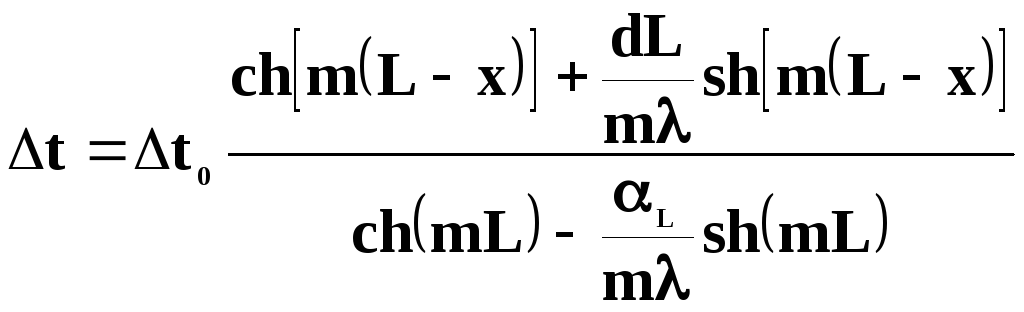, (Л3.13)

де враховано, що 0,5(е^mх + е^-mх ) =ch(mx)– гіперболічний косинус та

0,5(е^mх - е^-mх ) =sh(mx)– гіперболічний синус.

Якщо коефіцієнт теплопровідності λматеріалу стержня великий, наприклад, виготовленого із міді, алюмінію чи їх сплавів, а діаметрdстержня достатньо малий, то можна вважати [2], щоі тепловіддачею з торця стержня можна знехтувати. В цьому випадку умови однозначності розв’язку (Л3.10) можна записати:

приx=0Δt=Δt₀; (Л3.14)

при x=L.

За цих умов у залежності (Л3.13) другі члени чисельника та знаменника перетворюються на нуль і вираз (Л3.13) набуває вигляду:

, (Л3.15)

або в безрозмірній формі

, (Л3.16)

де

При x=L, оскількиch[m(L-L)]=ch0=1[1]. Для стаціонарного режиму теплопередачі кількість теплотиQ_p, яка віддається поверхнею стержня в навколишній простір, є рівною кількістю теплоти, що підводиться до основи стержня за рахунок теплопровідності:

(Л3.17)

Взявши похідну від виразу (Л3.15), знайдемо

, (Л3.18)

Звідки Q_p=λAmΔt₀th(mL).(Л3.19)

Для другого стержня , тоді

Q_p=0,785d²λmΔt₀th(mL).(Л3.20)