4. Дифференциал функции. Применение дифференциала к приближенным вычислениям

Пусть функция f(x) дифференцируема в точке х₀. Дифференциалом функции f(x) в точке х₀ называется главная часть приращения функции, линейно зависящая от приращения аргумента . Обозначаетсяdy, . Таким образом, согласно определению

.

Рассмотрим функцию ,, то есть для независимого аргументах дифференциал и приращение совпадают: .

Дифференциалом независимой переменной х называется ее приращение :.

Тогда из определения дифференциала следует

.

Из определения производной и дифференциала следует, что при малых справедливо приближенное равенство:или формула:

(5)

Пример 4.1. Вычислить приближенно: .

Решение. Для приближенного вычисления будем использовать формулу (5).

В нашем случае следует взять ,,. Выберемитак, чтобывычислялось легко, абыло достаточно мало по модулю:,.

Подставим эти значения в формулу (5):

Ответ: .

Пример 4.2. Вычислить приближенно .

Решение. Для приближенного вычисления будем использовать формулу (5)

В нашем случае следует взять ,,. Выберемитак, чтобывычислялось легко, абыло достаточно мало по модулю:,.

Подставим эти значения в формулу (5):

.

Ответ: .

5. Производные и дифференциалы высших порядков

Пусть функция y=f(x) определена на множестве D и существует . Тогда наD определена функция . Если эта функция имеет производную в точкеxD, то её называют производной второго порядка (или второй производной) функции f(x) в точке x.

Обозначается ,,,.

Таким образом .

Производные высших порядков определяются индуктивно. Если для любого существует, то наD определена функция . Производная от этой функции (если она существует) в точкеxD называется производной n–го порядка функции f(x) в точке x.

.

Обозначается: ,,,.

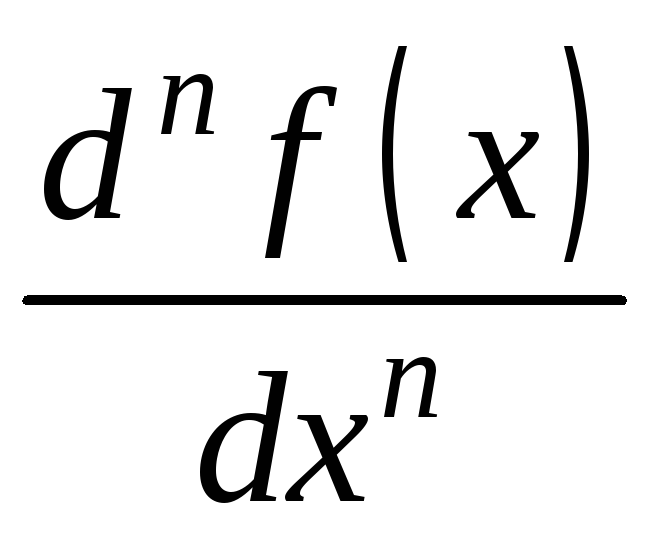Cчитают, что .

Заметим, что если существует в точкех, то в некоторой окрестности точки существуети все производные более низкого порядкаk, k<n.

Если для функции y=f(x) в точке х существует , то говорят, что функцияn раз дифференцируема в этой точке.

Пусть y=f(x) дважды дифференцируема на множестве D. Дифференциалом второго порядка функции f называется дифференциал от её дифференциала первого порядка и обозначается . Таким образом.

Если х – независимая переменная, то

.

Итак, .

Дифференциал любого порядка определяется индуктивно. Предположим, что уже введён дифференциал (n-1)–го порядка , и чтоy=f(x) дифференцируема n раз.

Дифференциалом n-го порядка функции f называется дифференциал от её дифференциала (n-1)-го порядка.

Обозначается . Т. о.,.

Аналогично, как для дифференциала второго порядка, получим

.

6. Правило Лопиталя

При раскрытии неопределенностей ,кроме классических методов вычисления пределов, во многих случаях можно пользоваться правилом Лопиталя:

Eсли или и существует предел отношения их производных , то.

Это правило справедливо и в случае .

Пример 6.1. Применяя правило Лопиталя, найти пределы:

а) ;б) ;в) .

Решение. Убедившись, что имеет место случай или, применяем правило Лопиталя.

а) ,

б) .

Здесь мы дважды применили правило Лопиталя и воспользовались первым замечательным пределом.

в) .

При раскрытии неопределенностей для применения правила Лопиталя, данное выражение надо преобразовать к неопределенностямилипутем алгебраических преобразований.

Пример 6.2. Найти пределы:

а) ;б) .

Решение: а) Имеем неопределенность . Приведем эту неопределенность к неопределенности, а затем применим правило Лопиталя:

.

б) Имеем неопределенность . Преобразуем к неопределенности, после чего применим правило Лопиталя:

.

При раскрытии неопределенностей ,,рекомендуется найти предварительно предел логарифма искомой функции.

Пример 6.3. Вычислить .

Решение. Имеем неопределенность . Введем обозначение

, тогда ..

Получили неопределенность , применяем правило Лопиталя:

.

Так как . Следовательно.

Пример 6.4. Пользуясь правилом Лопиталя, вычислить предел .

Решение. В данном случае имеется неопределенность , но от нее не удается избавится после однократного применения правила Лопиталя. В данном примере это правило приходится использовать три раза.

.