1.12. Проверка адекватности регрессионной модели

Регрессионная модель , построенная по результатам эксперимента, позволяет рассчитать значения отклика в разных точках области варьирования факторов.

Проверка адекватности математической модели дает возможность экспериментатору ответить на вопрос, будет ли построенная модель предсказывать значения выходной величины с той же точностью, что и результаты эксперимента.

Пусть – число опытов экспериментального плана, или число серий параллельных опытов, если опыты дублируются,– число оцениваемых коэффициентов регрессии математической модели.

Проверка адекватности возможна только при , т.е. если план эксперимента является ненасыщенным.

Для проверки адекватности модели необходимо знать оценку дисперсии воспроизводимости , которую можно вычислить, в зависимости от методики дублирования опыта (см. 1.11).

1.13. Порядок проверки адекватности модели

1. Определяют сумму квадратов, характеризующую адекватность модели . При равномерном дублировании опытов

,

где – число дублированных опытов в каждой серии,– среднее значение результатов в-той серии дублированных результатов,– теоретическое значение, вычисленное с помощью полученной регрессионной модели.

В случае неравномерного дублирования

,

–число дублированных опытов в -той серии.

2. Вычисляют число степеней свободы дисперсии адекватности. При любой методике дублировании.

3.Вычисляют дисперсию адекватности

(19)

С помощью -критерия Фишера проверяют однородность дисперсии адекватности (18) и дисперсии воспроизводимости (19). При этом вычисляют

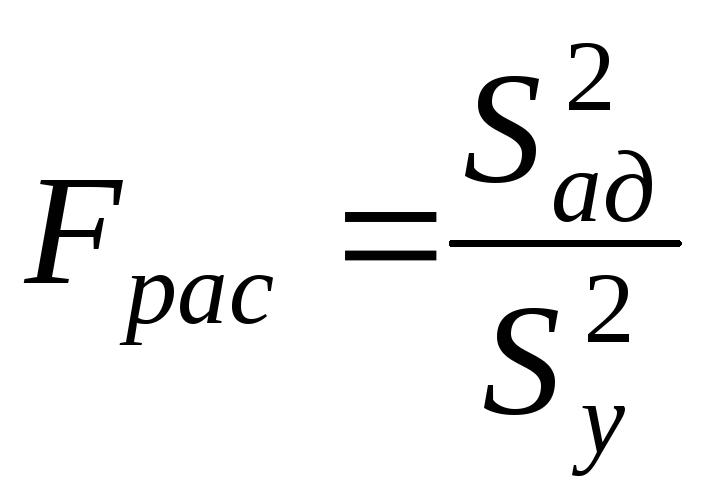, (20)

которое сравнивается с табличным значением , найденным при выбранном уровне значимости для чисел степеней свободы , в числителе ив знаменателе ().

Если , то модель считается адекватной и может быть использована для описания объекта. В противном случае модель не адекватна.

Рассмотренный метод проверки адекватности играет простой физический смысл.

В основе этой процедуры лежит проверка гипотезы об однородности дисперсии адекватности и дисперсии, характеризующей ошибку эксперимента. Заметим, что дисперсия адекватности характеризует расхождение между результатами эксперимента и значениями выходной величины, вычисленными по уравнению регрессии. Очевидно, что модель удовлетворительно описывает объект исследования, т.е. является адекватной, если указанное расхождение вызвано только экспериментальными ошибками, а не связано, например, с неудачным выбором вида математической модели.

Проверка гипотезы об однородности рассматриваемых дисперсий и выясняет общность происхождения экспериментальных ошибок и расхождения между и.

1.14. Коэффициент детерминации

В качестве меры того, насколько хорошо регрессия описывает данную систему наблюдений, служит коэффициент детерминации.

Коэффициент детерминации интегрально характеризует точностные свойства уравнения регрессии. Он показывает, какая доля из общего рассеяния экспериментальных значений относительно своего среднего, обусловлена регрессионной зависимостью:

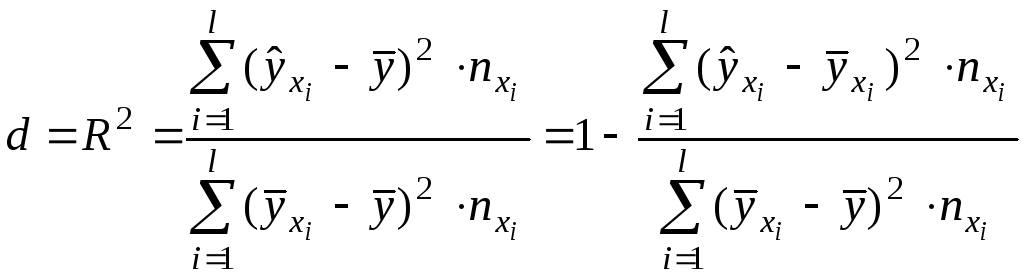, (21)

где – теоретическое значение результативного признака, вычисленное с помощью полученной регрессионной модели,– среднее значение,– среднее групповое, т.е. фактические значения результативного признака.

.

Если , то вариацияполностью определяется случайными возмущениями, а влияние факторане обнаруживается.

Если , регрессионная кривая проходит через все экспериментальные точки. Можно указать некоторую нижнюю границу коэффициента детерминации, имея ввиду, что лишь в случае, когдауравнение регрессии представляет достаточный практический интерес:. Если, то регрессионная модель вряд ли работоспособна.