1.5. Свойства выборочного коэффициента корреляции

1. Абсолютная величина выборочного коэффициента корреляции не превосходит 1 ().

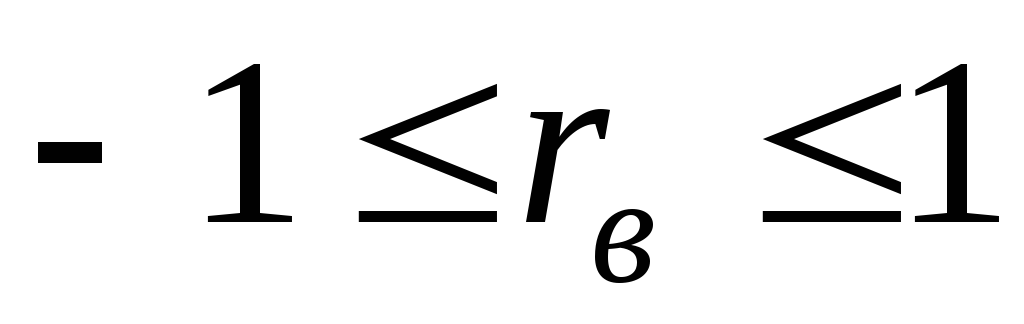2. Если выборочный коэффициент корреляции равен 0 и выборочные линии регрессии – прямые линии, то 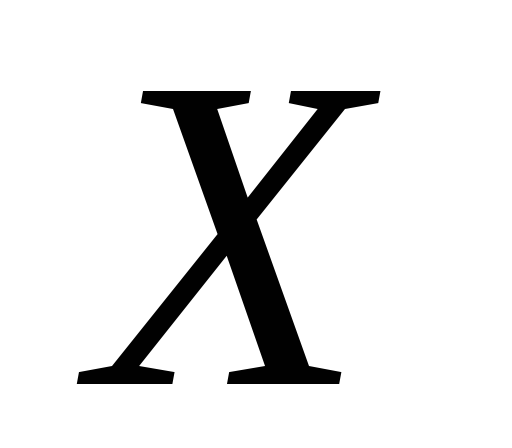и не связаны линейной корреляционной зависимостью и , .

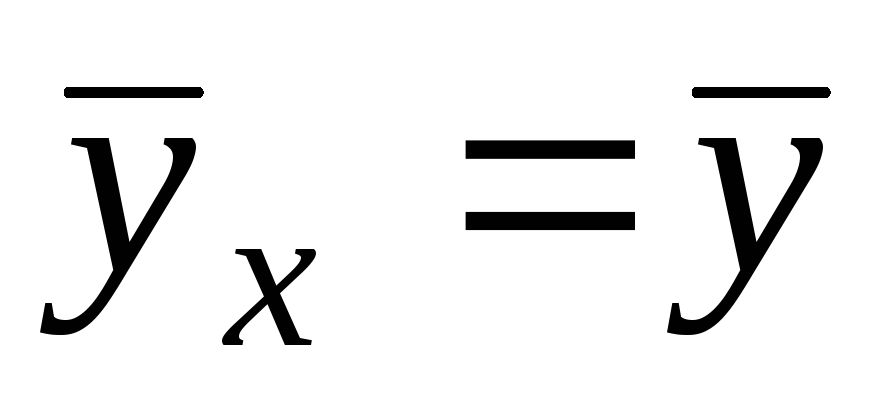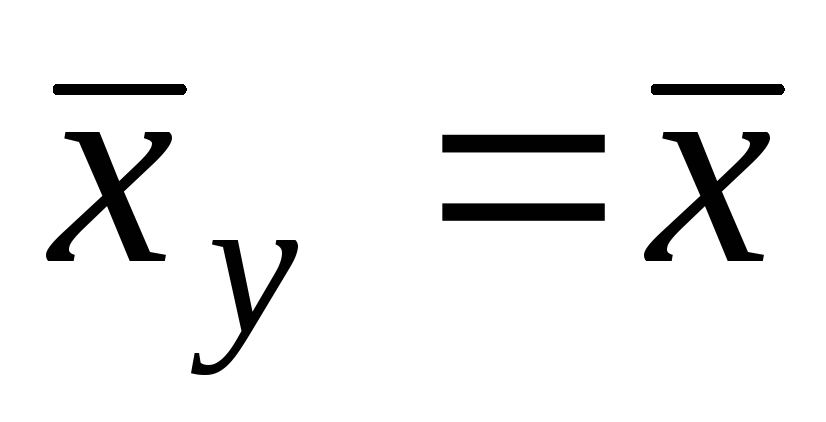В этом случае прямые линии регрессии параллельны соответственно координатным осям.

Замечание. Если выборочный коэффициент корреляции , то признакии могут быть связаны нелинейной корреляционной или даже функциональной зависимостью.

3. Если абсолютная величина 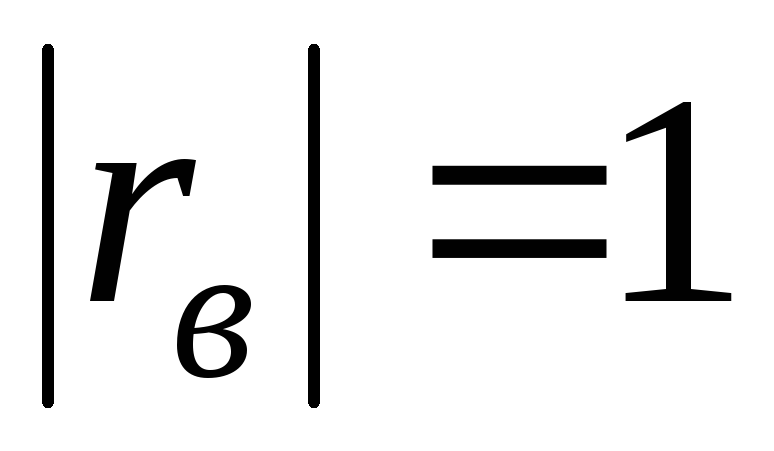, то наблюдаемые значения признаков связаны линейной функциональной зависимостью.

4. С возрастанием абсолютной величины выборочного коэффициента корреляции линейная корреляционная зависимость становится более тесной и при 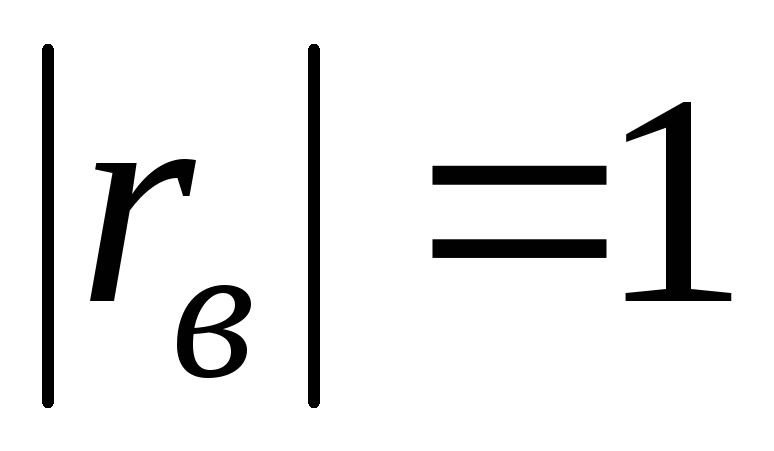переходит в функциональную.

Величина коэффициента корреляции характеризует силу линейной связи между признаками ():

если – связь слабая;

если – связь умеренная;

если – связь заметная;

если – связь высокая;

если – связь весьма высокая;

если – связь функциональная.

5. Знак выборочного коэффициента корреляции совпадает со знаком выборочного коэффициента регрессии: , и определяет направление связи. Если – связь прямая,– связь обратная.

Перемножим первое и второе равенства ; .

Знак при радикале должен совпадать со знаком коэффициента регрессии, т.е. , если;, если.

Выборочный коэффициент корреляции равен среднему геометрическому выборочных коэффициентов регрессий.

1.6. Точечная и интервальная оценки коэффициентов корреляции нормально распределенной генеральной совокупности

Если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность, то заключение о тесноте линейной зависимости между признаками, полученное по данным выборки, в известной степени может быть распространено на генеральную совокупность. В качестве точечной оценки коэффициента корреляции генеральной совокупности берут.

Для интервальной оценки коэффициента корреляции нормально распределенной генеральной совокупности () имеем:

. (8)

1.7. Проверка гипотезы о значимости выборочного коэффициента корреляции

Пусть двумерная генеральная совокупность , распределена нормально. Из этой совокупности извлечена выборка объема и по ней найден выборочный коэффициент корреляции, который оказался отличным от 0.

Так как выборка отобрана случайно, то еще нельзя заключить, что коэффициент корреляции генеральной совокупности также отличен от 0.

Нас интересует именно этот коэффициент . Поэтому возникает необходимость при заданном уровне значимости проверить нулевую гипотезу о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе.

Если гипотеза будет опровергнута, то это означает, что выборочный коэффициент корреляции значительно отличается от 0, а и связаны линейной зависимостью.

Если нулевая гипотеза будет принята, то выборочный коэффициент корреляции не значим, а и не связаны линейной зависимостью.

В качестве критерия проверки нулевой гипотезы примем случайную величину 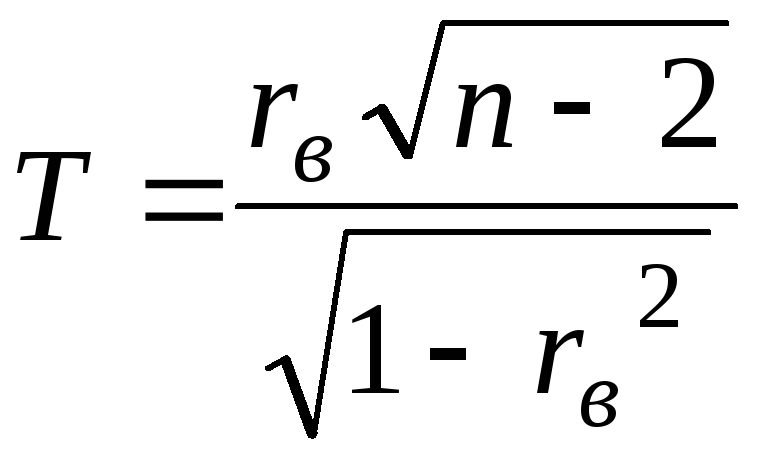, где– объем выборки.

Величина при справедливости нулевой гипотезы имеет распределение Стьюдента сстепенями свободы. Обозначим значение критерия, вычисленное по данным наблюдений черези сформулируем правило проверки нулевой гипотезы.

Для того чтобы при заданном уровне значимости проверить нулевую гипотезуо равенстве нулю генерального коэффициента корреляции нормальной двумерной случайной величины, при конкурирующей гипотезенадо вычислить наблюдаемое значение критерия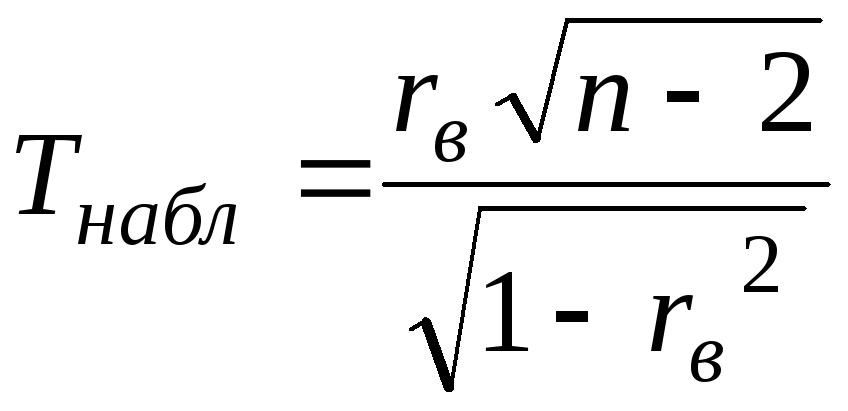и по таблице критических точек распределения Стьюдента по заданному уровню значимостии числу степеней свободынайти критическую точкудлядвусторонней критической области.

Если – нет основания отвергнуть нулевую гипотезу. Если– нулевую гипотезу отвергают и, следовательно, выборочный коэффициент корреляции значимо отличается от 0 , то естьи линейно корреляционны.