Варианты расчетно-графической работы

Задание 1. Изменить порядок интегрирования.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

17. .

18. .

19. .

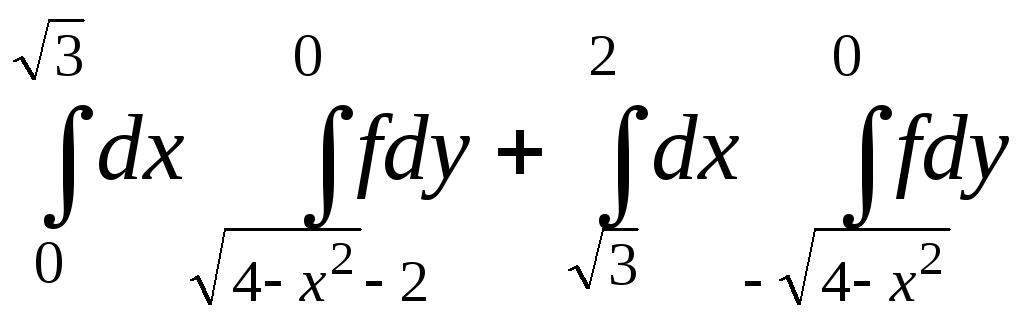20. .

21. .

22. .

23. .

24. .

25. .

26. .

27. .

28. .

29. .

30. .

Задание 2. Вычислить двойной интеграл.

1. ; .

2. ; .

3. ; .

4. ; .

5. ; .

6. ; .

7. ; .

8. ; .

9. ; .

10. ; .

11. ; .

12. ; .

13. ; .

14. ; .

15. ; .

16. ; .

17. ; .

18. ; .

19. ; .

20. ; .

21. ; .

22. ; .

23. ; .

24. ; .

25. ; .

26. ; .

27. ; .

28. ; .

29. ; .

30. ; .

Задание 3. Найти площадь фигуры, ограниченной данными линиями.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12..

13. .

14. .

15. .

16. .

17. .

18. .

19. .

20. .

21. .

22. .

23. .

24. .

25. .

26. .

27. .

28. .

29. .

30. .

Задание 4. Пластинка D задана ограничивающими ее кривыми,  - поверхностная плотность. Найти массу пластинки.

1. ; .

2. ; .

3. ; .

4. ; .

5. ; .

6. ; .

7. ; .

8. ; .

9. D: х=1, y=0, y²=4х (y0); .

10. D: x²+y²=1, x²+y²=9, x=0, y=0 (x0, y0);= (x-y)/(x²+y²).

11. D: x=1, y=0, y²=x (y0);=3x+6y².

12. D: x²+y²=9, x²+y²=25, x=0, y=0 (x;=(2y-x)/(x²+y²).

13. D: x=2, y=0, y²=x/2 (y0);=2x+3y².

14. D: x²+y²=4, x²+y²=16, x=0, y=0 (x;=(2y-3x)/(x²+y²).

15. D: x=, y=0, y²=8x (y0);= 7x+3y².

16. D: x²+y²=9, x²+y²=16, x=0, y=0 (x;=(2y-5x)/(x²+y²).

17. D: x=1, y=0, y²=4x (y0);= 7x²+2y.

18. D: x²+y²=1, x²+y²=16, x=0, y=0 (x;=(x+3y)/(x²+y²).

19. D: x=2, y²=2x, y=0 (y0);=7x²/4+y/2.

20. D: x²+y²=1, x²+y²=4, x=0, y=0 (x;=(x+2y)/(x²+y²).

21. D: x=2, y=0, y²=2x (y0);= 7x²/4+y.

22. D: x²+y²=1, x²+y²=9, x=0, y=0 =(2x-y)/(x²+y²).

23. D: x=2, y=0, y²=x/2 (y0);= 7x²/2+8y.

24. D: x²+y²=1, x²+y²=25, x=0, y=0 =(x-4y)/(x²+y²).

25. D: x=1, y= 0, y²=4x (y;= 6x+3y².

26. D: x²+y²=4, x²+y²=16, x=0, y=0 =(3x-y)/(x²+y²).

27. D: x=2, y= 0, y²=x/2 (y;= 4x+6y².

28. D: x²+y²=4, x²+y²=9, x=0, y=0 (x;=(y-4x)/(x²+y²).

29. D: x=1/2, y= 0, y²=2x (y;= 4x+9y².

30. D: x²+y²=4, x²+y²=9, x=0, y=0 (x;=(y-2x)/(x²+y²).

Задание 5. Найти объем тела, заданного ограничивающими его поверхностями.

1. y=16, y=, z=0, x+z=2.

2. y=5, y=5x/3, z=0, z=5+5.

3. x²+y²=2, y= , y=0, z=0, z=15x.

4. x+y=2, y=, z=12y, z=0.

5. x=20, x=5, z=0, z+y=1/2.

6. x=5, x=5y/6, z=0, z=.

7. x²+y²=2, x=, x=0, z=0, z=30y.

8. x+y=2, x=, z=12x/5, z=0.

9. y=17, y=2, z=0, x+z=1/2.

10. y=5, y=5x/9, z=0, z=5(3+)/9.

11. x²+y²=8, y=, y=0, z=0, z=15x/11.

12. x+y=4, y=, z=3y, z=0.

13. x=, x=, z=0, z=.

14. x=19, x=4, z=0, z+y=2.

15. x²+y²=8, x=, x=0, z=30y/11, z=0.

16. x+y=4, x=, z=3x/5, z=0.

17. y=6, y=, z=0, x+z=3.

18. y=, y=, z=0, z=.

19. x²+y²=18, y=, y=0, z=0, z=5x/11.

20. x+y=6, y=, z=4y, z=0.

21. x=7, x=2, z=0, z+y=3

22. x=5, x=5y/9, z=0, z=5(3+)/9.

23. x²+y²=18, x=, x=0, z=0, z=10y/11.

24. x+y=6, x=, z=4x/5, z=0.

25. y=, , z=0, z=(1+).

26. x²+y²=50, y=, y=0, z=0, z=3x/11.

27. x+y=8, y=, z=3y, z=0.

28. x=16, x=, z+y=2, z=0.

29. x=15, x=15y, z=0, z=15(1+).

30. x²+y²=50, x=, x=0, z=0, z=6y/11.

Задание 6. Вычислить тройной интеграл.

1. x dx dy dz ;

V: y=10x, y=0, x=1, z=xy, z=0.

2. ;

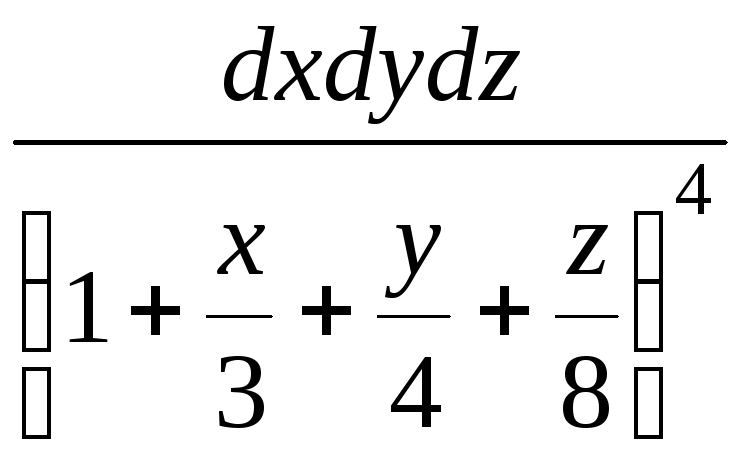V: , x=0, y=0, z=0.

3. 15(y²+z²) dx dy dz;

V: z=x+y, x+y=1, x=0, y=0, z=0.

4. (3x+4y) dx dy dz;

V: y=x, y=0, x=1, z=5(x²+y²), z=0.

5. (1+2x³) dx dy dz;

V: y=9x, y=0, x=1, z=, z=0.

6. (27+54y³) dx dy dz;

V: y=x, y=0, x=1, z=, z=0.

7. y dx dy dz;

V: y=15x, y=0, x=1, z=xy, z=0.

8. ;

V: , x=0, y=0, z=0.

9. (3x²+y²) dx dy dz;

V: z=10y, x+y=1, x=0, y=0, z=0.

10. (15x+30z) dx dy dz;

V: z=x²+3y², z=0, y=x, y=0, x=1.

11. (4+8z³) dx dy dz;

V: y=x, y=0, x=1, z=, z=0.

12. (1+2x³) dx dy dz;

V: y=36x, y=0, x=1, z=, z=0.

13. 21xz dx dy dz;

V: y=x, y=0, x=2, z=xy, z=0.

14. ;

V: x/10+y/8+z/3=1, x=0, y=0, z=0.

15. (x²+3y²) dx dy dz;

V: z=10x, x+y=1, x=0, y=0, z=0.

16. (60y+90z) dx dy dz;

V: y=x, y=0, x=1, z=x²+y², z=0.

17. dx dy dz;

V: y=9x, y=0, x=1, z=, z=0.

18. (9+18z) dx dy dz;

V: y=4x, y=0, x=1, z=, z=0.

19. 3y² dx dy dz;

V: y=2x, y=0, x=2, z=xy, z=0.

20. ;

V: x/2+y/4+z/6=1, x=0, y=0, z=0.

21. x² dx dy dz;

V: z=10(x+3y), x+y=1, x=0, y=0, z=0.

22. (8y+12z) dx dy dz;

V: y=x, y=0, x=1, z=3x²+2y², z=0.

23. 63(1+2) dx dy dz;

V: y=x, y=0, x=1, z=, z=0.

24. (x+y) dx dy dz;

V: y=x, y=0, x=1, z=30x²+60y², z=0.

25. ;

V: x/6+y/4+z/16=1, x=0, y=0, z=0.

26. xyz dx dy dz;

V: y=x, y=0, x=2, z=xy, z=0.

27. y² dx dy dz;

V: z=10(3x+y), x+y=1, x=0, y=0, z=0.

28. dx dy dz;

V: y=x, y=0, x=1, z=x²+15y², z=0.

29. (x²+4y²) dx dy dz;

V: z=20(2x+y), x+y=1, x=0, y=0, z=0.

30. ;

V: x/8+y/3+z/5=1, x=0, y=0, z=0