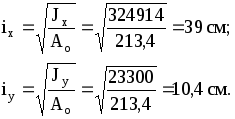4. Расчет колонны

Расчетные усилия в сечениях левой колонны приведены в табл. 2.Для верхней части колонны в сечении 1-1 М = 1116 кНм; N = 849 кН; в сечении 2-2 при том же сочетании нагрузок (1, 2, 4, 6, 8) М = 169 кНм. Для нижней части колонны М₁ = 950 кНм; N₁ = -3454 кН (сечение 3-3 изгибающий момент догружает подкрановую ветвь); М₂ = -1861 кНм; N₂ = -1894 кН (сечение 4-4 изгибающий момент догружает наружную ветвь); Q_max = 201,5 кН.

Соотношение жесткостей верхней и нижней частей колонны J_в/J_н = 1/5; материал колонны - сталь С 245, бетон фундамента - В 12,5. Конструктивная схема колонны показана на рис. 13.

4.1. Определение расчетных длин колонны в плоскости действия момента

Расчетные длины _ef1 (нижней части колонны) и _ef2 (верхней части колонны) определяем по формуле (67) [4]

_ef1 = ₁₁; _ef2 = ₂₂.

Так как ₁/₂ = H_в/H_н = 6,42/11,18 = 0,57 < 0,6 и N₁/N₂ = N_н/N_в = 3454/849 = 4 > 3 значения коэффициентов ₁ и ₂ определяем по табл.18 [4].

При принятом жестком сопряжении ригеля с колонной верхний конец колонны закреплен только от поворота, поэтому коэффициенты ₁ = 2, а ₂ = 3.

Примечание: если H_в/H_н = 0,6 или N_н/N_в < 3 то значения коэффициентов ₁ и ₂ следует определять по п.6.11* и прил.6 [4].

Таким образом, для нижней части колонны

_ef1 = ₁₁ = 211,18 = 22,36 м;

для верхней

_ef2 = ₂₂ = 36,42 = 19,26 м.

4.2. Подбор сечения верхней колонны

Сечение верхней части колонны в соответствии с п. 1.2. принято в виде сварного двутавра высотой h_в = 900 мм.

Абсолютный эксцентриситет

м = 130 см.

Радиус инерции

см.

Ядровое расстояние

см.

Относительная гибкость

.

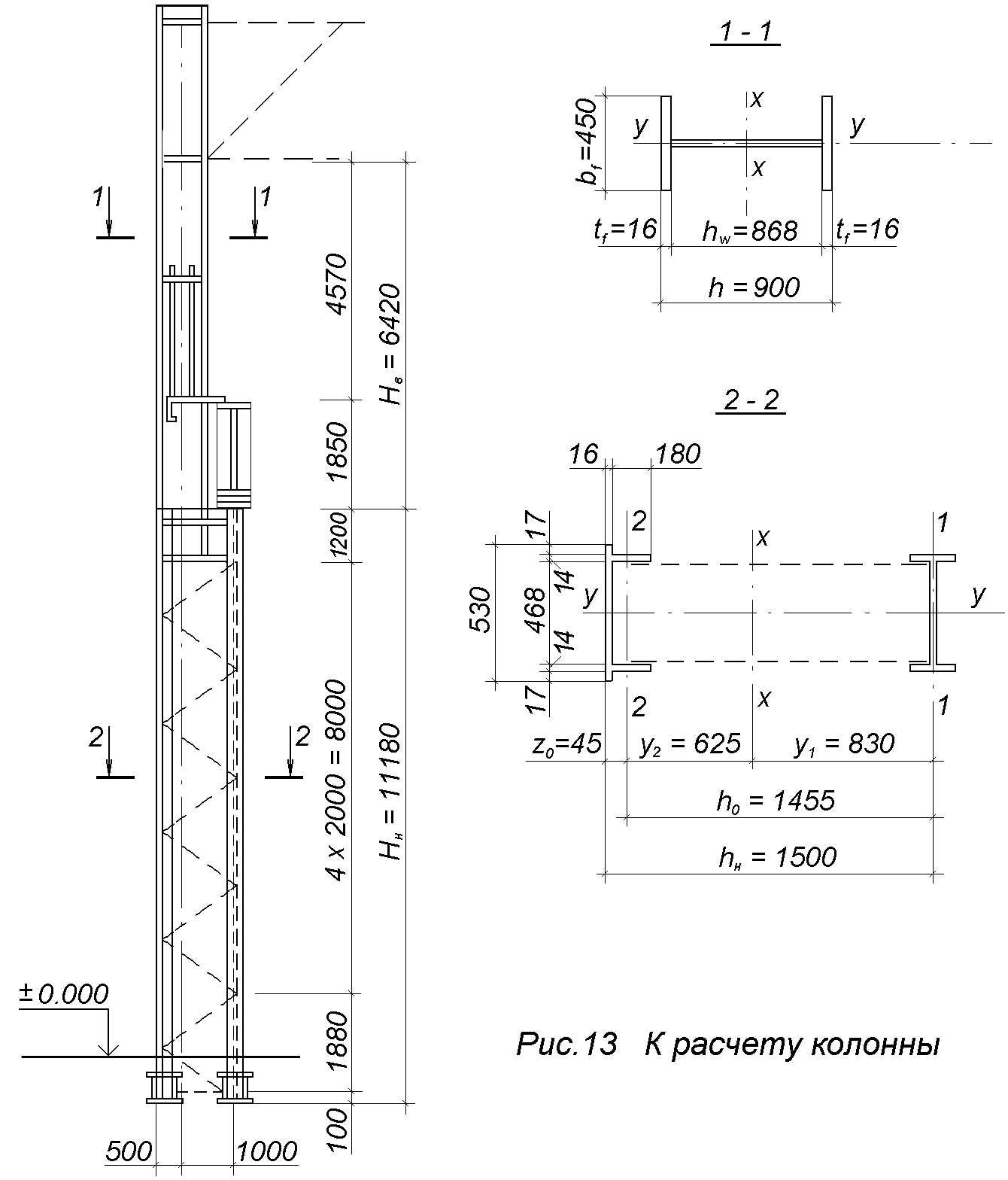
Относительный эксцентриситет

.

Коэффициент влияния формы сечения определяем по табл.73 [4]. Примем в первом приближении А_f/А_w = 1: 1,425

Приведенный относительный эксцентриситет m_f определяем по формуле

m_f = m = 1,425·4,13 = 5,88.

По табл.74 [4] при = 1,66 иm_ef = 5,88; _е = 0,206

см².

Высота стенки (принимаем предварительно толщину полок t_f= 16мм)

h_w = h_в - 2t_f = 90 - 21,6 = 86,8 см

Предельное отношение расчетной высоты стенки к толщине [h_w/t_w]:

по табл.27* при m = 4,13 > 1 и = 1,66 < 2

= 1,3 + 0,15= 1,3 + 0,151,66² = 1,71 < 3,1.

(если _uw > 3,1, то следует принимать _uw = 3,1)

t_w = h_w/51 = 1,7 см.

Примечание: если иm  1 или m < 1 _uw следует определять по табл.27*

Поскольку сечение с такой толстой стенкой неэкономично, принимаем t_w = 8 мм (h_w/t_w = 86,8/0,8 = 108 > [h_w/t_w] = 51 ); в расчет включаем только часть площади стенки и в расчетных формулах за значение А принимаем значения А_red, вычисленное с высотой стенки h_red.

Условная гибкость стенки

;

коэффициент

k = 1,2+0,15= 1,2+0,151,66 = 1,45 (при >3,5 следует принимать=3,5).

h_red вычисляем в соответсвии с п.7.20 по формуле (92,б)

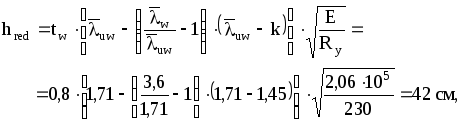
Требуемая площадь поясов

см².

Принимаем полки из широкополочной универсальной стали 450 х 16; А_f = 72 см² ≈ А_f.тр = 72,7 см².

Из условия местной устойчивости по табл.29* [4]

т.е. устойчивость обеспечена.

Геометрические характеристики сечения (рис. 13):

Полная площадь сечения

А_о = 2b_ft_f + t_wh_w = 2451,6 + 0,886,8 = 213,4 см²;

расчетная площадь сечения с учетом только устойчивой части стенки:

А = 2b_ft_f + h_red t_w = 2451,6 + 420,8 = 177,6 см².

Момент инерции сечения относительно оси х-х

Момент инерции сечения относительно оси y-y

Момент сопротивления

см³

Ядровое расстояние

см

Радиусы инерций