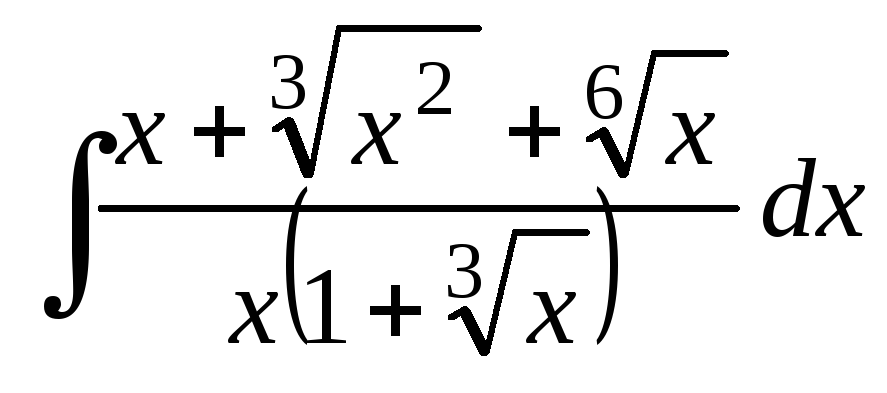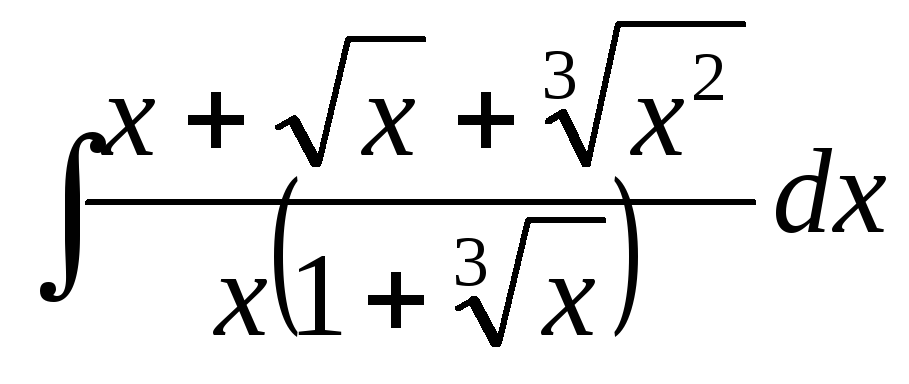-
Метод Остроградского
Пусть знаменатель
несократимой дроби
имеет вид
.
Метод Остроградского заключается в использовании формулы
.
В ней многочлены
и
имеют вид
,
соответственно и
могут быть вычислены без разложения
многочлена
на произведение неприводимых множителей.
Действительно,
является наибольшим общим делителем
двух многочленов
и
,
и может быть вычислен при помощи алгоритма
Евклида, который излагается в курсе
алгебры.
Остается вычислить
многочлены
и
как многочлены с неопределенными
коэффициентами степени на единицу ниже,
чем
и
соответственно. Для вычисления указанных
неопределенных коэффициентов следует
продифференцировать формулу Остроградского,
привести результат дифференцирования
к общему знаменателю и сопоставить
коэффициенты при одинаковых степенях
х в числителях.
Метод Остроградского
особенно эффективен, когда корни
в основном являются кратными или когда
вызывает затруднение нахождение корня
.
Вычислим
.
Имеем
,
.
Наибольший общий делитель этих многочленов равен
.
Поделив
на
«столбиком», найдем
.
и
задаем как многочлены первой степени
с неопределенными коэффициентами, и
формула Остроградского принимает вид
Продифференцируем эту формулу:
.
Результат дифференцирования приводим к общему знаменателю, после чего сопоставляем числители. Получим
.
Сопоставляя
коэффициенты при
и
,
получим систему уравнений:
Решая эту систему,
найдем
.
Таким образом формула Остроградского
принимает вид:
.
Вычислим интеграл в правой части:
.
Окончательно имеем
.
Рассмотрим еще один пример.
Разложим знаменатель на множители:
.
Отсюда
.
.
Приравнивая коэффициенты:
.
.
Упражнение. Применяя метод Остроградского найти соответствующие интегралы из расчетно-графической работы.
-
Тригонометрические функции
При интегрировании тригонометрических функций часто оказываются полезными следующие формулы
;
;
.
Например,
.
Иногда удобно
использовать формулу
следующим образом:
.
Рассмотрим интеграл вида
С рациональной функцией R.
При любой функции
такой интеграл сводится к интегралу от
рациональной функции с помощью
универсальной тригонометрической
подстановки
.
.
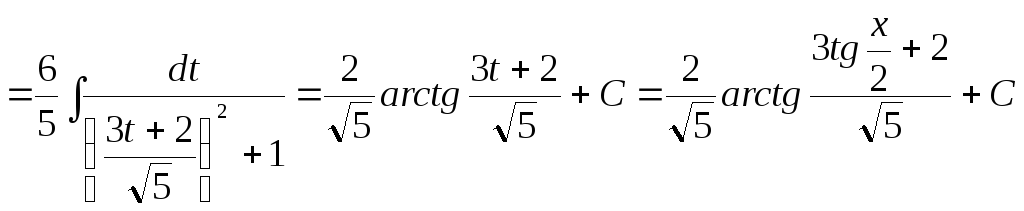В некоторых случаях
процедуру сведения интеграла
к интегралу от рациональной функции
можно упростить. Рассмотрим эти случаи.
1) Если
,
то удобнее воспользоваться постановкой
.
2) При условии
,
проще всего использовать замену
.
3) В случае
,
поможет подстановка
.
Например,
.
Интеграл вида
можно рационализировать посредством
подстановки
,
при этом
.
Упражнение. Решить соответствующие задания из расчетно-графической работы.
-
Интегрирование иррациональных функций.
Если подынтегральная
функция содержит радикалы вида
,
,
,
то часто бывает полезно сделать одну
из следующих замен:
,
,
или
,
,
.
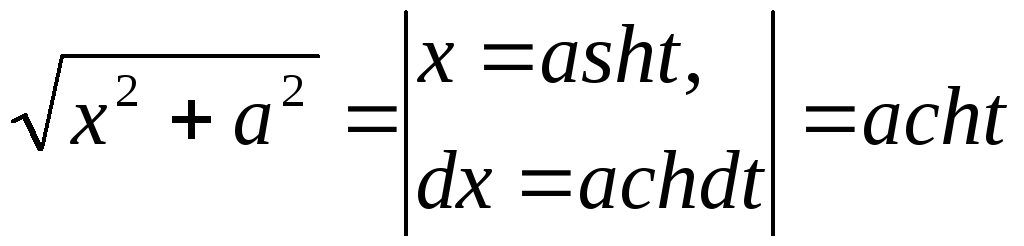В следующем интеграле воспользуемся последней из замен
.
Иногда могут помочь тригонометрические или гиперболические подстановки другого вида:
.
Упражнение. Решить соответствующие интегралы из расчетно-графической работы.
Рассмотрим интеграл вида:
.
Выделим из
рациональной функции целую часть
,
и разложим правильную
дробь
на сумму простейших дробей. После этого
задача о нахождении интеграла сводится
к нахождению интегралов:
1)
2)
,
3)
Первый интеграл считается с помощью формулы
.
Чтобы найти
коэффициенты многочлена
степени n-1 и число
надо продифференцировать эту формулу.
.
После дифференцирования получим
.
Приравниваем коэффициенты
.
Отсюда,
.
.
Посчитаем теперь
второй интеграл с помощью замены
.
Получим
.
Таким образом, второй интеграл сведен к предыдущему.
Осталось рассмотреть
третий интеграл. В случае
делаем замену
.
Когда
,
нужна замена
,
при этом
и
подбираются такими, чтобы в трехчленах
не осталось членов с первой степенью.
Для этого надо решить относительно
и
уравнения.
,
.
После замены получим интегралы
.
В первом из них
применим подстановку
,
во втором - подстановку
.
Рассмотрим
соответствующие примеры. Первый случай
:
.
Случай второй (
:
.
Решаем систему
,
.
,
.
Делаем замену
,
,
.
Дальше интеграл считается совершенно аналогично предыдущему.
Интеграл вида
,
,
,
где
- рациональная функция, можно свести к
интегралу от рациональных функций
посредством одной из подстановок
Эйлера:
,
a>0,
,
c>0,
,
,
где
один
из корней квадратного трехчлена
.
.
.
.
.
.
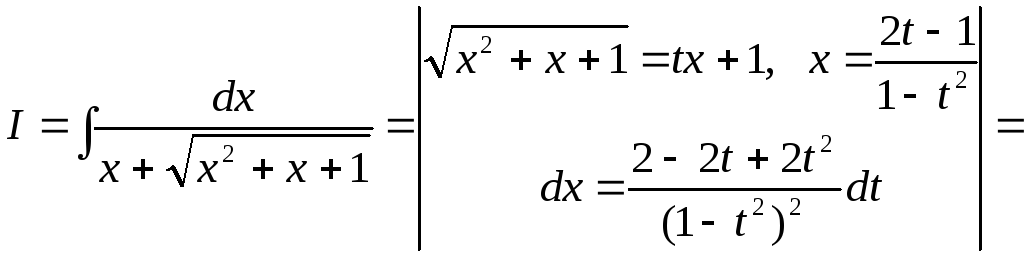
Упражнение. С помощью подстановки Эйлера вычислить соответствующие интегралы из расчетно-графической работы.
Интегралы вида
,
где
,
,
причем
,
называют интегралом от дифференциального
бинома. Данный интеграл сводится к
интегралу от рациональной функции в
следующих трех случаях:
- подстановкой
,
где
- общий знаменатель m
, n;
- подстановкой
,
где q – знаменатель
р;
- подстановкой
,
где q – знаменатель
р.
Рассмотрим пример
.
Здесь
,
.
,
,
.
Делаем замену
,
,
.
Тогда
.
Этот интеграл вычисляется также как интегралы в пп. 4, 5
Упражнение. Вычислить соответствующие интегралы от дифференциального бинома входящие в расчетно-графическую работу.
|
Найти неопределенные интегралы (в пунктах 1.1-1.5 результаты проверить дифференцированием) 1.1 |
1.2 |
||||
|
10. |
11. |
|
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20. |
21.
22.
23.
24.
25.
26.
27.
28.
29.
30. |
|
1.3 |
1.4 |
||||
|
|
|
|
|
|
|
|
1.5 |
1.6 |
||||
|
|
|
|
|
|
|
|
1.7 |
1.8 |
||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
1.9 |
1.10 |
||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
11 |
1.12 |
||||
|
|
|
|
|
|
|
|
1.13 |
1.14 |
||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10. |
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
2.1 |
2.2 |
||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
2.3 |
2.4 |
||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10. |
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
2.5 |
2.6 |
||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
2.7 |
2.8 |
||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
2.9 |
2.10 |
||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
3.1 |
3.2 |
||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20. |
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
3.3 |
3.4 |
||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
3.6 |
||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
3.5 |
||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
3.7 |
3.8 |
||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
4.1 |
||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
4.2 |
||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
4.3 |
||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
4.4 |
||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
4.5 |
4.6 |
||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
4.7 |
||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
|
|
|
|
4.8 |
||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
4.9 |
||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
