Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Брянская государственная инженерно-технологическая академия»
Муравьев а.Н., Котова и.А.
Интегрирование функций
одной переменной
Методические указания и задания
к выполнению расчетно-графической работы для студентов
экономического факультета
БРЯНСК 2012
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Брянская государственная инженерно-технологическая академия»
Утверждены редакционным
Советом БГИТА
Протокол N от ___________
Интегрирование функций
одной переменной
Методические указания и задания
к выполнению расчетно-графической работы для студентов
экономического факультета
Брянск 2012
Составител: Муравьев А. Н.
Котова И.А.
Компьютерный набор: Муравьев А. Н., Котова И.А.
Рецензент: к.ф.-м. наук, профессор Евтюхов К.Н.
Рекомендованы редакционной комиссией
механико – технологического факультета
Протокол N от __________________
Рассматриваются основные теоретические сведения, связанные с понятием неопределенного интеграла, его свойствами и методами интегрирования. Приводятся подробные вычисления интегралов на примерах. Приведены задания для расчетно-графической работы.
Методические указания предназначены для студентов 1-го курса экономического факультета.
Содержание
-
Таблица простейших интегралов ……………………………………… 3
-
Замена переменной ……………………………………………………... 5
-
Интегрирование по частям ……………………………………………... 8
-
Интегрирование рациональных функций ………………….…………. 12
-
Метод Остроградского …………………………………………………. 15
-
Тригонометрические функции ………………………………………… 20
-
Интегрирование иррациональных функций ………………………….. 22
-
Задания для расчетно-графической работы ……………………….….. 25
-
Примеры выполнения заданий РГР …………….……………………... 50
-
Таблица простейших интегралов
Определение 1.
Функция F называется
первообразной для функции f
на множестве Х, если для всех
.
В дальнейшем множество Х указывать
не будем. Совокупность всех первообразных
для функции
называется
неопределенным интегралом этой
функции и обозначается
.
Если
первообразная для
,
то
,
где С - произвольная константа.
ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
; 
;
;
;
ТАБЛИЦА ПРОСТЕЙШИХ ИНТЕГРАЛОВ
,
,
,
,
, 
,
, 
,
, 
,
,
,
,
,
,
,
,
.
Приведем некоторые примеры вычисления неопределенных интегралов.
.
Проверим результаты интегрирования. Найдем производную функцию от полученного результата.
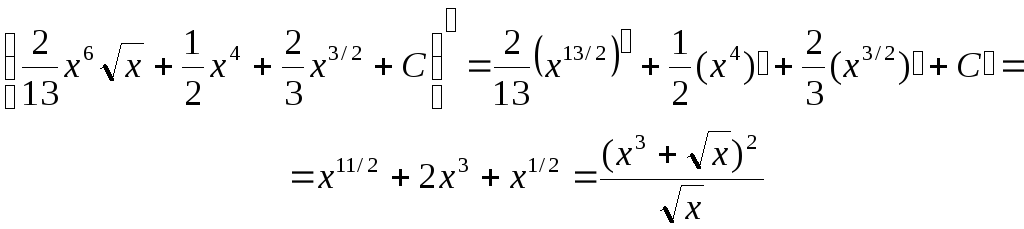
Упражнение. Применяя таблицу простейших интегралов выполнить задания 1-5 из расчетно-графической работы. Результаты интегрирования проверить дифференцированием.