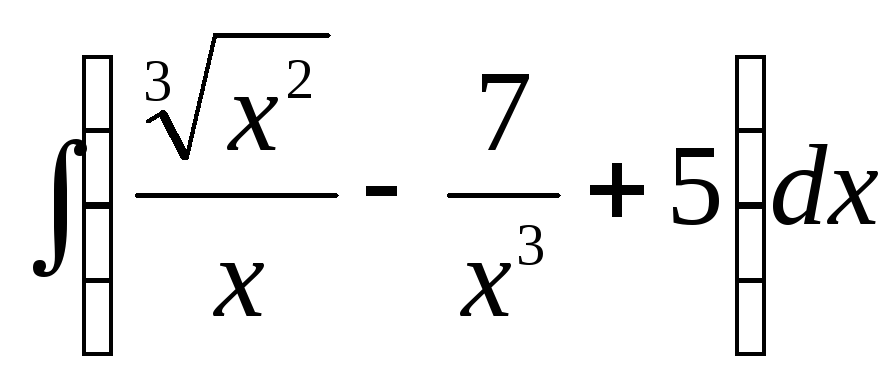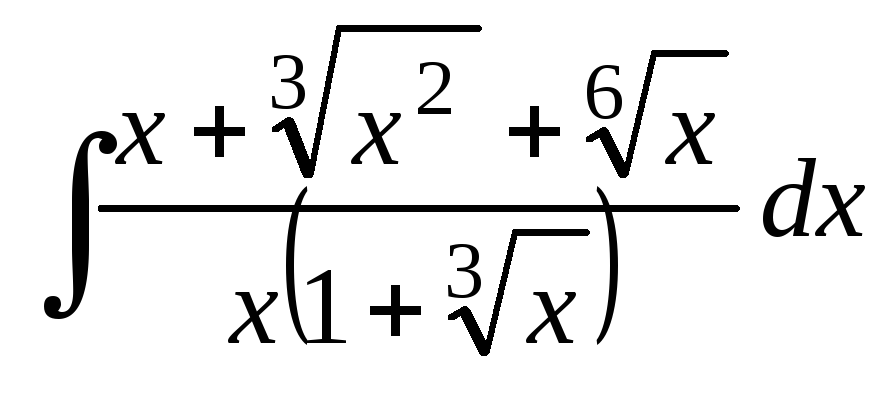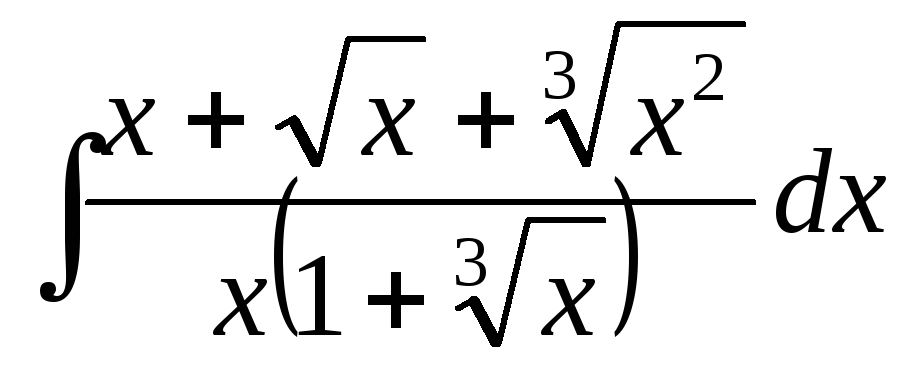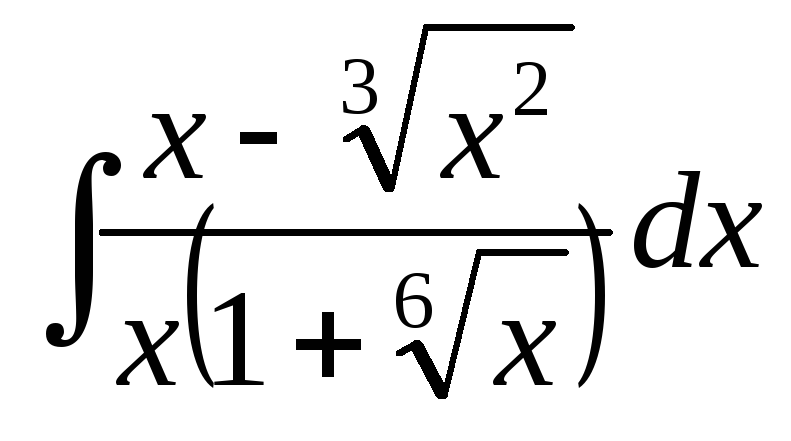Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Брянская государственная инженерно-технологическая академия»
Муравьев а.Н., Котова и.А.
Интегрирование функции одной переменной
Методические указания и задания
к расчетно-графической работы для студентов
всех направлений подготовки бакалавров

БРЯНСК 2012
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Брянская государственная инженерно-технологическая академия»
Утверждены редакционным
Советом БГИТА
Протокол Nот ___________
Интегрирование функции
одной переменной
Методические указания и задания
к расчетно-графической работы для студентов
всех направлений подготовки бакалавров
Брянск 2012
Составител: Муравьев А. Н.
Котова И.А.
Компьютерный набор: Муравьев А. Н., Котова И.А.
Рецензент: к.ф.-м. наук, профессор Евтюхов К.Н.
Рекомендованы редакционной комиссией
механико – технологического факультета
Протокол Nот __________________
Рассматриваются основные теоретические сведения, связанные с понятием неопределенного интеграла, его свойствами и методами интегрирования. Приводятся подробные вычисления интегралов на примерах. Приведены задания для расчетно-графической работы.
Методические указания предназначены для студентов 1-го курса.
Содержание
Таблица простейших интегралов ……………………………………… 6
Замена переменной ……………………………………………………... 7
Интегрирование по частям ……………………………………………... 9
Интегрирование рациональных функций ………………….…………. 11
Метод Остроградского …………………………………………………. 14
Тригонометрические функции ………………………………………… 17
Интегрирование иррациональных функций ………………………….. 19
Задания для расчетно-графической работы ……………………….….. 24
Примеры выполнения заданий РГР …………….……………………... 47
Таблица простейших интегралов
Определение 1.
ФункцияFназываетсяпервообразнойдля функцииfна множествеХ, если для всех![]() .
В дальнейшем множествоХуказывать
не будем. Совокупность всех первообразных
для функции
.
В дальнейшем множествоХуказывать
не будем. Совокупность всех первообразных
для функции![]() называетсянеопределенным интеграломэтой
функции и обозначается
называетсянеопределенным интеграломэтой
функции и обозначается![]() .
Если
.
Если![]() первообразная для
первообразная для![]() ,
то
,
то![]() ,
гдеС- произвольная константа.
,
гдеС- произвольная константа.
ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
![]() ;
; ![]() ;
;
![]() ;
;
![]() ;
;
ТАБЛИЦА ПРОСТЕЙШИХ ИНТЕГРАЛОВ
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]()
![]() .
.
Приведем некоторые примеры вычисления неопределенных интегралов.
![]()
![]() .
.
Проверим результаты интегрирования. Найдем производную функцию от полученного результата.
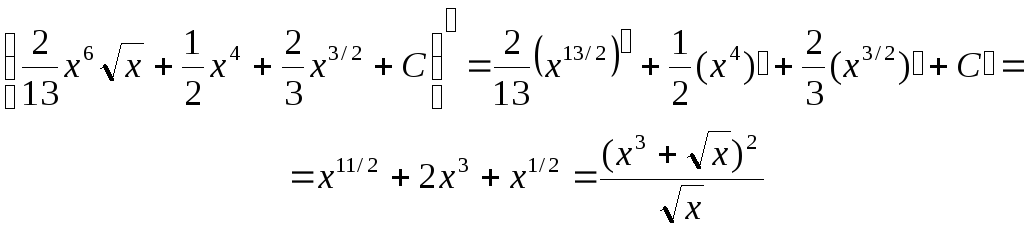
Упражнение.Применяя таблицу простейших интегралов выполнить задания 1-5 из расчетно-графической работы. Результаты интегрирования проверить дифференцированием.
Замена переменной
Используя формулу
для дифференциала функции
![]() ,
с помощью замены
,
с помощью замены![]() часто удается упростить интегральное
выражение вида
часто удается упростить интегральное
выражение вида
![]() ,
,
где
![]() - первообразная для функции
- первообразная для функции![]() .
.
Приведем некоторые формулы для преобразования дифференциалов:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Рассмотрим несколько примеров.
![]()
![]() .
.
![]()
![]() .
.
Иногда при интегрировании функции, содержащей в знаменателе неразложимые квадратные трехчлены (с отрицательными дискриминантами), надо выделить в трехчлене полный квадрат. Общее правило выделения полного квадрата в неразложимом трехчлене:
![]() .
.
Рассмотрим простейшие примеры.
![]()
![]() .
.
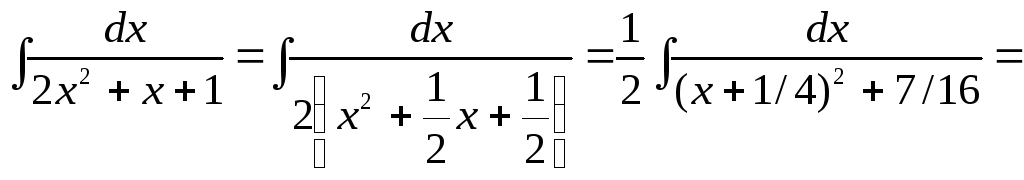
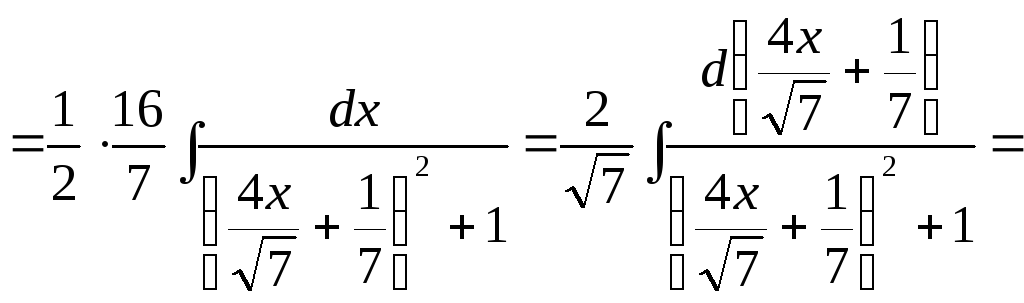
![]() .
.
Иногда удобнее
проводить замену переменных в обратном
порядке. Пусть
![]() и
и![]() взаимообратные и непрерывно дифференцируемые
функции. Если -
взаимообратные и непрерывно дифференцируемые
функции. Если -![]() первообразная для функции
первообразная для функции![]() ,
то
,
то
![]() .
.
Функция
![]() подбирается так, чтобы упростить
подынтегральное выражение.
подбирается так, чтобы упростить
подынтегральное выражение.
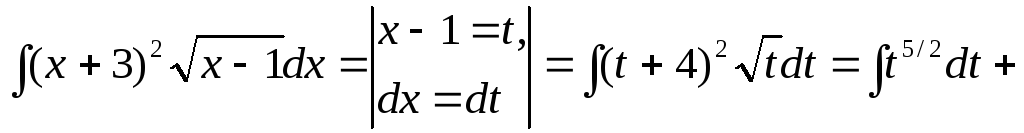
![]()
![]() .
.
Если дробных
степеней от выражений
![]() несколько, то делаем замену
несколько, то делаем замену
![]() ,
,
где р– наибольший общий знаменатель всех показателей степеней.
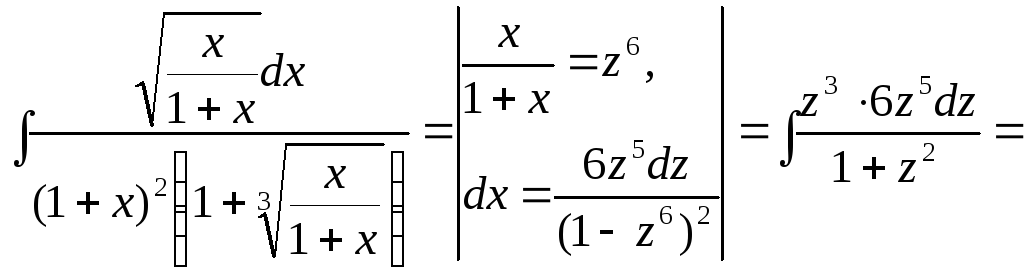
![]()
![]()
![]() .
.
При этом мы разделили
![]() на
на![]() .
.
Вычислим еще несколько интегралов.
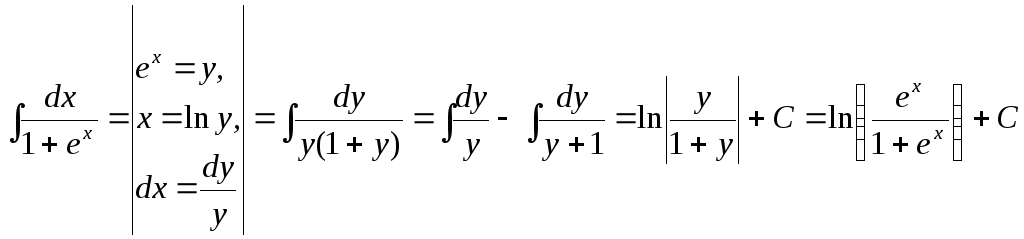 .
.
![]() .
.
Интегрирование по частям
Если
![]() ,
,![]() - непрерывно дифференцируемые функции,
то справедлива формула интегрирования
по частям
- непрерывно дифференцируемые функции,
то справедлива формула интегрирования
по частям
![]() или
или
![]() .
.
Приведем наиболее типичные примеры.
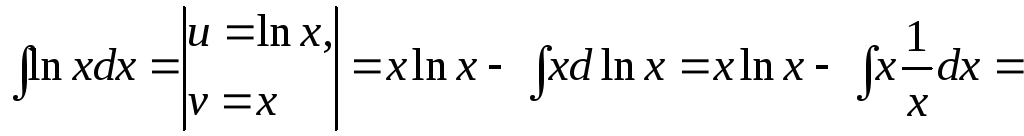
![]() .
.
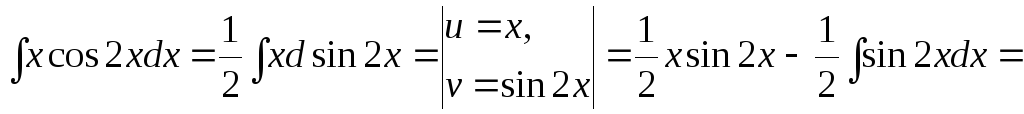
![]() .
.
![]()
![]() .
.
Такие интегралы
аналогичным образом вычисляются и в
случае, когда в первом интеграле вместо
множителя
![]() или во втором интеграле вместо множителя
или во втором интеграле вместо множителя![]() стоит некоторый многочлен степениn.
При этом надо интегрировать последовательно
по частямnраз.
стоит некоторый многочлен степениn.
При этом надо интегрировать последовательно
по частямnраз.
Интегралы следующих типов выражаются сами через себя.
![]()
![]()
![]()
![]()
![]() .
.
Отсюда,
![]() ,
,
![]() .
.
![]()
![]()
![]() .
.
Поэтому,
![]() ,
,
![]() .
.
Упражнение.Применяя метод интегрирования по частям, выполнить соответствующие задания из расчетно-графической работы.
Интегрирование рациональных функций
Рациональной
называется функция вида
![]() ,
,
где
![]() и
и![]() - многочлены степени
- многочлены степени![]() и
и![]() соответственно,
соответственно,![]() .
Поэтому интегрирование рациональных
функций сводится к интегрированию
многочлена и правильной рациональной
дроби
.
Поэтому интегрирование рациональных
функций сводится к интегрированию
многочлена и правильной рациональной
дроби
![]() ,
,
![]() .
.
При этом можно
считать коэффициент при
![]() равным единице.
равным единице.
Первым шагом при вычислении интеграла от функции такого вида является разложение знаменателя на множители
![]() ,
,
где
![]() - корни многочлена
- корни многочлена![]() кратности
кратности![]() соответственно, а трехчлены
соответственно, а трехчлены![]() ,
,![]() не имеют действительных корней
не имеют действительных корней![]() .
При этом
.
При этом![]() .
.
Следующим шагом является представление дроби в виде суммы простейших дробей:
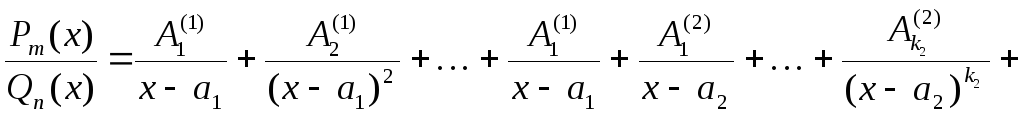
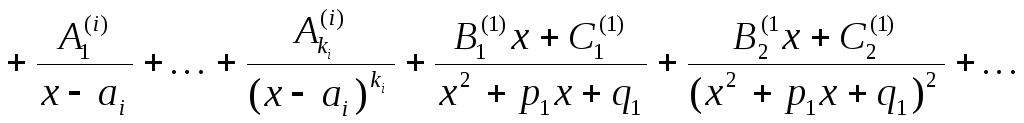
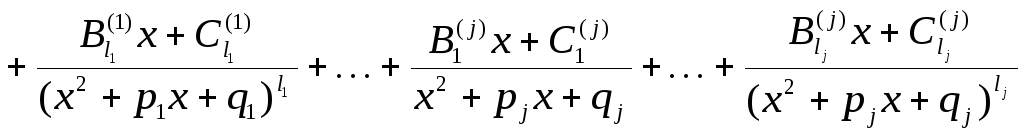 .
.
Здесь
![]() - некоторые числа, которые находятся
методом неопределенных коэффициентов.
Заключается он в том, что правая часть
последнего равенства приводится к
общему знаменателю. В числителе
получившегося выражения получается
некоторый многочлен степени
- некоторые числа, которые находятся
методом неопределенных коэффициентов.
Заключается он в том, что правая часть
последнего равенства приводится к
общему знаменателю. В числителе
получившегося выражения получается
некоторый многочлен степени![]() ,
коэффициенты которого, выраженные через
искомые константы, надо приравнять к
коэффициентам многочлена
,
коэффициенты которого, выраженные через
искомые константы, надо приравнять к
коэффициентам многочлена![]() .
Получается система
.
Получается система![]() линейного уравнения. Рассмотрим пример
линейного уравнения. Рассмотрим пример
![]()
![]()
![]() .
.
![]()
![]() .
.
Отсюда
![]()
![]()
![]() .
.
Решая эту систему,
получим значения
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
Поэтому
.
Поэтому
![]() .
.
Есть другие методы нахождения коэффициентов разложения, которые не столь универсальны, как изложенный выше, но в в частных случаях бывают гораздо удобнее. Например, если знаменатель имеет только действительные простые (кратности один) корни, можно поступить следующим образом.
![]() .
.
![]() .
.
Положим поочередно
![]() .
Получим равенства
.
Получим равенства
![]() .
.
Отсюда
![]() .
.
![]() .
.
Если знаменатель имеет действительные корни, среди которых есть корни кратности больше единицы, то поступим так:
![]() .
.
![]() .
.
Положим
![]() ,
тогда
,
тогда![]() .
Теперь положим
.
Теперь положим![]() ,
получим
,
получим![]() .
Осталось найти А. Продифференцируем
предыдущее тождество:
.
Осталось найти А. Продифференцируем
предыдущее тождество:
![]() .
.
Положим
![]() равным значению кратного корня, т.е.
равным значению кратного корня, т.е.![]() ,
тогда
,
тогда
![]() .
.
![]()
![]() .
.
Итак, разбивая правильную дробь на простейшие, мы ее интегрирование сводим к интегрированию дробей следующих видов:
1)
![]() ; 2)
; 2)![]() ; 3)
; 3)![]() ; 4)
; 4)![]() .
.
Посчитаем интегралы от этих дробей:
1)
![]() ; 2)
; 2)![]() ;
;
3)
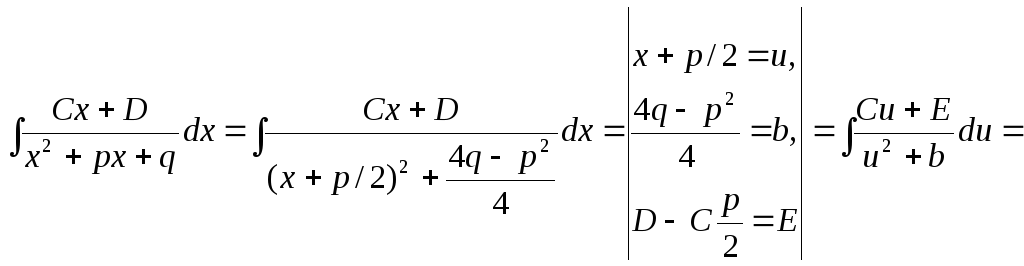
![]()
![]() .
.
Здесь надо заметить,
что
![]() так как
так как![]() - дискриминант квадратного трехчлена
- дискриминант квадратного трехчлена![]() ,
не имеющего действительных корней, а
значит, отрицательный.
,
не имеющего действительных корней, а
значит, отрицательный.
4)
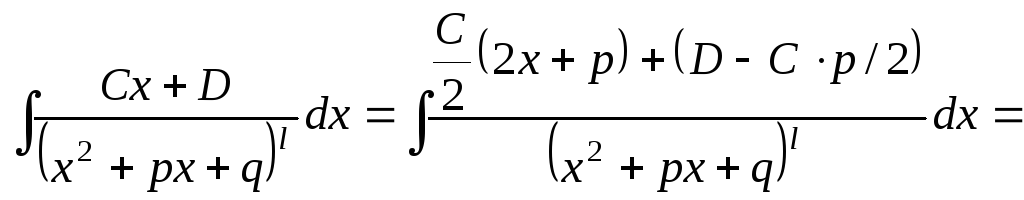
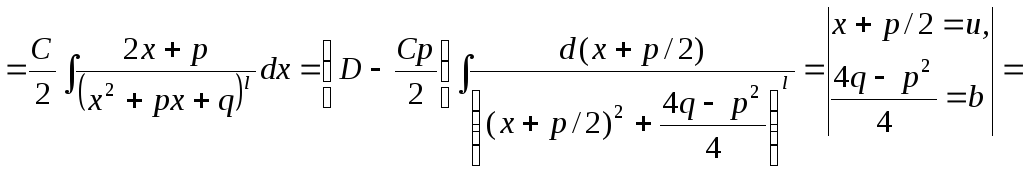
![]() .
.
В последнем
интеграле делается подстановка
![]() :
:
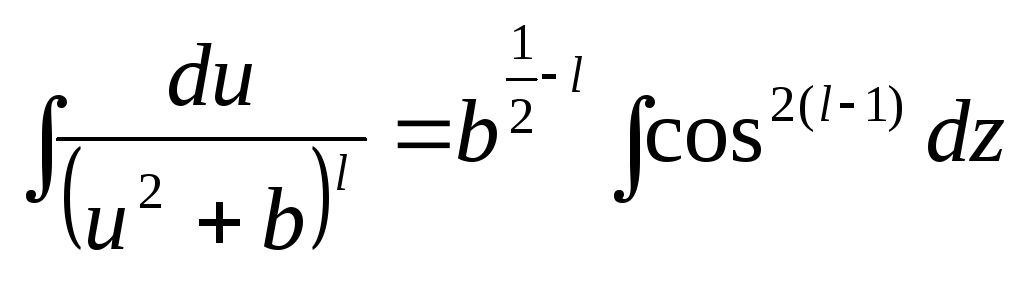 .
.
Вычисление такого интеграла рассмотрим в п. 6.
Еще один способ
вычисления интеграла
![]() - использовать рекуррентное соотношение,
которое сейчас установим.
- использовать рекуррентное соотношение,
которое сейчас установим.
![]()
![]()
![]() .
.
Например, посчитаем интеграл
![]() .
Следовательно, вышеприведенный интеграл
окончательно имеет вид:
.
Следовательно, вышеприведенный интеграл
окончательно имеет вид:
![]()
![]() .
.
Упражнение. Решить соответствующие задания из расчетно-графической работы.
Метод Остроградского
Пусть знаменатель
несократимой дроби
![]() имеет вид
имеет вид
![]() .
.
Метод Остроградского заключается в использовании формулы
![]() .
.
В ней многочлены
![]() и
и![]() имеют вид
имеют вид
![]() ,
,
![]()
соответственно и
могут быть вычислены без разложения
многочлена
![]() на произведение неприводимых множителей.
на произведение неприводимых множителей.
Действительно,
![]() является наибольшим общим делителем
двух многочленов
является наибольшим общим делителем
двух многочленов![]() и
и![]() ,
и может быть вычислен при помощи алгоритма
Евклида, который излагается в курсе
алгебры.
,
и может быть вычислен при помощи алгоритма
Евклида, который излагается в курсе
алгебры.
Остается вычислить
многочлены
![]() и
и![]() как многочлены с неопределенными
коэффициентами степени на единицу ниже,
чем
как многочлены с неопределенными
коэффициентами степени на единицу ниже,
чем![]() и
и![]() соответственно. Для вычисления указанных
неопределенных коэффициентов следует
продифференцировать формулу Остроградского,
привести результат дифференцирования
к общему знаменателю и сопоставить
коэффициенты при одинаковых степеняхх в числителях.
соответственно. Для вычисления указанных
неопределенных коэффициентов следует
продифференцировать формулу Остроградского,
привести результат дифференцирования
к общему знаменателю и сопоставить
коэффициенты при одинаковых степеняхх в числителях.
Метод Остроградского
особенно эффективен, когда корни
![]() в основном являются кратными или когда
вызывает затруднение нахождение корня
в основном являются кратными или когда
вызывает затруднение нахождение корня![]() .
.
Вычислим
![]() .
.
Имеем
![]() ,
,![]() .
.
Наибольший общий делитель этих многочленов равен
![]() .
.
Поделив
![]() на
на![]() «столбиком», найдем
«столбиком», найдем
![]() .
.
![]() и
и
![]() задаем как многочлены первой степени
с неопределенными коэффициентами, и
формула Остроградского принимает вид
задаем как многочлены первой степени
с неопределенными коэффициентами, и
формула Остроградского принимает вид
![]()
![]()
Продифференцируем эту формулу:
![]()
![]() .
.
Результат дифференцирования приводим к общему знаменателю, после чего сопоставляем числители. Получим
![]() .
.
Сопоставляя
коэффициенты при
![]() и
и![]() ,
получим систему уравнений:
,
получим систему уравнений:
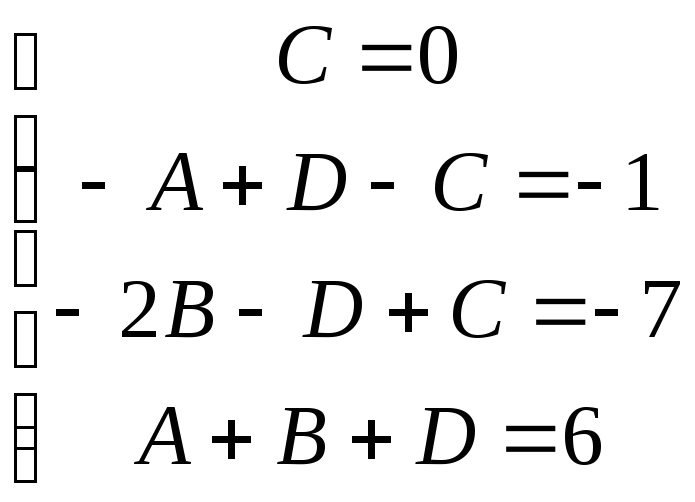
Решая эту систему,
найдем
![]() .
Таким образом формула Остроградского
принимает вид:
.
Таким образом формула Остроградского
принимает вид:
![]() .
.
Вычислим интеграл в правой части:
![]() .
.
Окончательно имеем
![]() .
.
Рассмотрим еще один пример.
![]()
Разложим знаменатель на множители:
![]() .
.
Отсюда
![]() .
.
![]() .
.
Приравнивая коэффициенты:
![]()
![]() .
.
![]()
![]() .
.
Упражнение. Применяя метод Остроградского найти соответствующие интегралы из расчетно-графической работы.
Тригонометрические функции
При интегрировании тригонометрических функций часто оказываются полезными следующие формулы
![]() ;
;
![]()
![]() ;
;
![]()
![]() .
.
Например,
![]()
![]()
![]() .
.
Иногда удобно
использовать формулу
![]() следующим образом:
следующим образом:
![]()
![]() .
.
Рассмотрим интеграл вида
![]()
С рациональной функцией R.
При любой функции
![]() такой интеграл сводится к интегралу от
рациональной функции с помощьюуниверсальной тригонометрической
подстановки
такой интеграл сводится к интегралу от
рациональной функции с помощьюуниверсальной тригонометрической
подстановки
![]() .
.
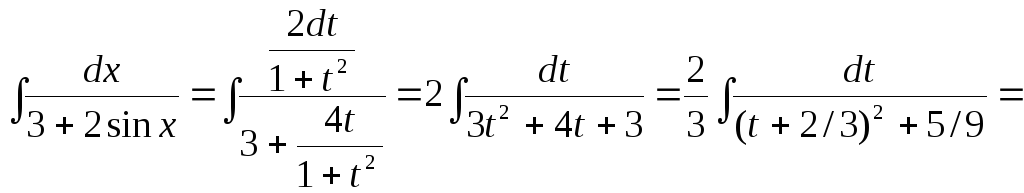
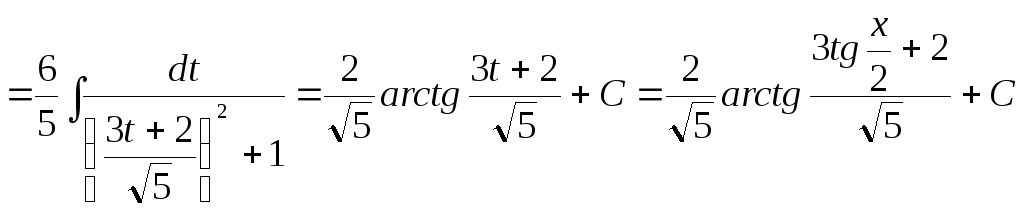 .
.
В некоторых случаях
процедуру сведения интеграла
![]() к интегралу от рациональной функции
можно упростить. Рассмотрим эти случаи.
к интегралу от рациональной функции
можно упростить. Рассмотрим эти случаи.
1) Если
![]() ,
то удобнее воспользоваться постановкой
,
то удобнее воспользоваться постановкой
![]() .
.
2) При условии
![]() ,
проще всего использовать замену
,
проще всего использовать замену
![]() .
.
3) В случае
![]() ,
поможет подстановка
,
поможет подстановка
![]() .
.
Например,
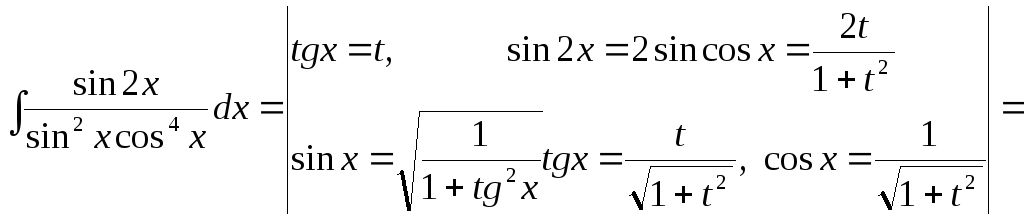
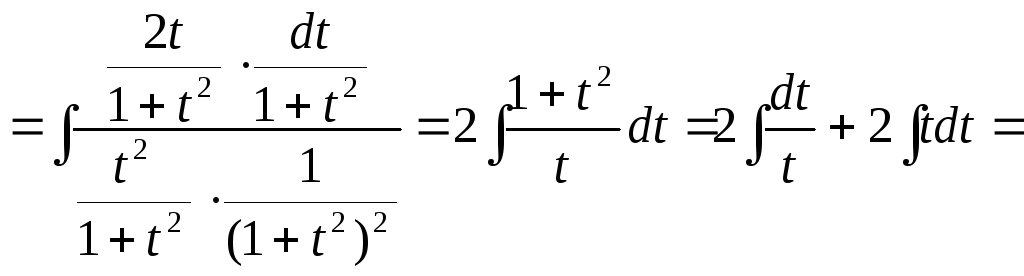
![]() .
.
Интеграл вида
![]() можно рационализировать посредством
подстановки
можно рационализировать посредством
подстановки![]() ,
при этом
,
при этом
![]() .
.
Упражнение. Решить соответствующие задания из расчетно-графической работы.
Интегрирование иррациональных функций.
Если подынтегральная
функция содержит радикалы вида
![]() ,
,![]() ,
,![]() ,
то часто бывает полезно сделать одну
из следующих замен:
,
то часто бывает полезно сделать одну
из следующих замен:
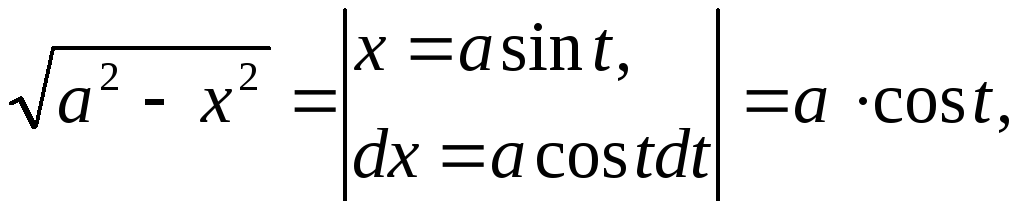
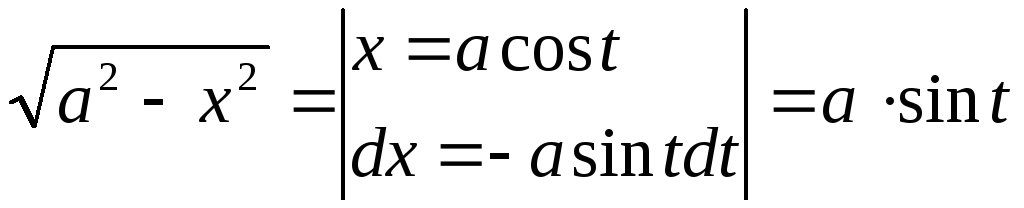 ,
,
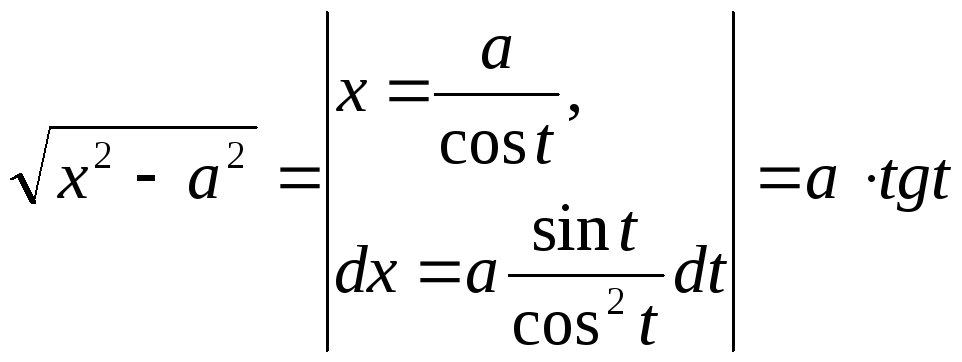 ,
,
или
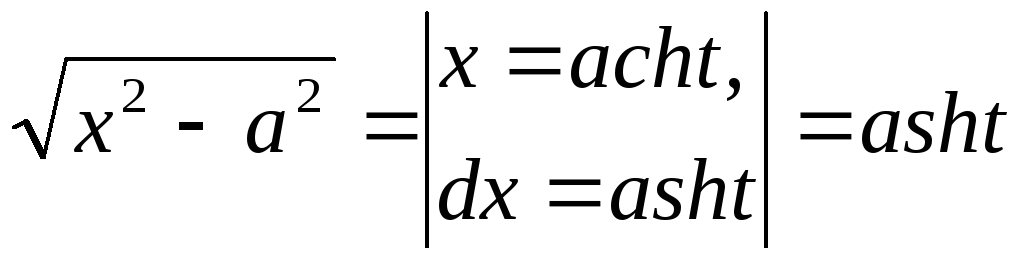 ,
,
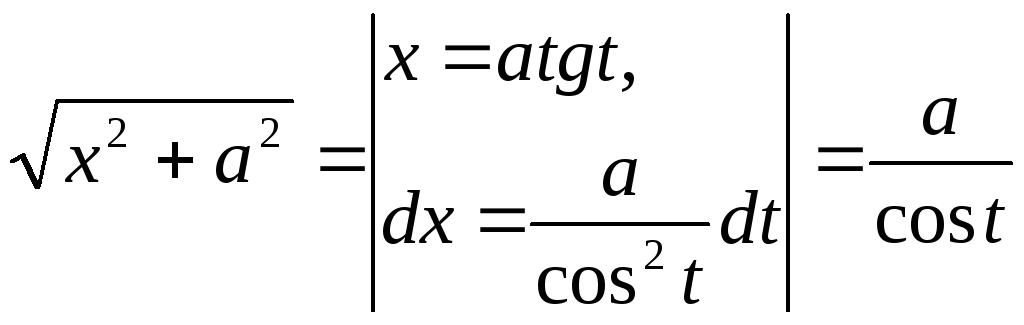 ,
,
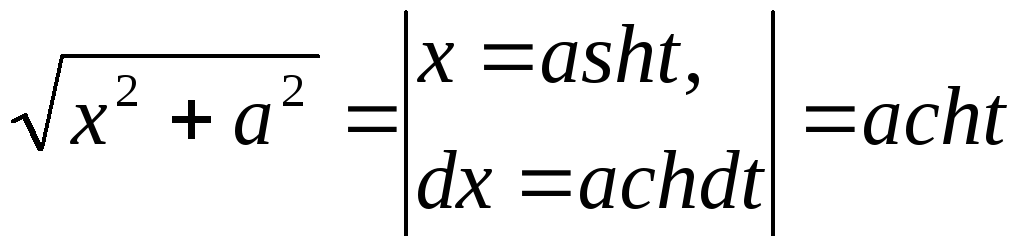 .
.
В следующем интеграле воспользуемся последней из замен
![]() .
.
Иногда могут помочь тригонометрические или гиперболические подстановки другого вида:
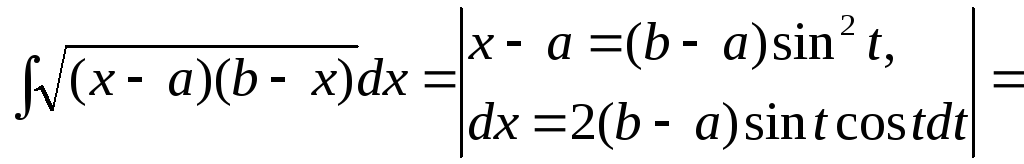
![]()
![]()
![]()
![]() .
.
Упражнение. Решить соответствующие интегралы из расчетно-графической работы.
Рассмотрим интеграл вида:
![]() .
.
Выделим из
рациональной функции целую часть
![]() ,
,
и разложим правильную
дробь
![]() на сумму простейших дробей. После этого
задача о нахождении интеграла сводится
к нахождению интегралов:
на сумму простейших дробей. После этого
задача о нахождении интеграла сводится
к нахождению интегралов:
1)![]() 2)
2)![]() ,
3)
,
3)![]()
Первый интеграл считается с помощью формулы
![]() .
.
Чтобы найти
коэффициенты многочлена
![]() степениn-1и число
степениn-1и число![]() надо продифференцировать эту формулу.
надо продифференцировать эту формулу.
![]() .
.
После дифференцирования получим
![]() .
.
Приравниваем коэффициенты
![]() .
.
Отсюда,
![]() .
.
![]()
![]() .
.
Посчитаем теперь
второй интеграл с помощью замены
![]() .
.
Получим
![]()
![]()
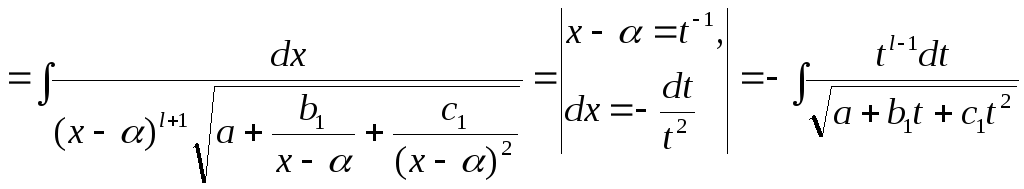 .
.
Таким образом, второй интеграл сведен к предыдущему.
Осталось рассмотреть
третий интеграл. В случае
![]() делаем замену
делаем замену![]() .
Когда
.
Когда![]() ,
нужна замена
,
нужна замена![]() ,
при этом
,
при этом![]() и
и![]() подбираются такими, чтобы в трехчленах
не осталось членов с первой степенью.
Для этого надо решить относительно
подбираются такими, чтобы в трехчленах
не осталось членов с первой степенью.
Для этого надо решить относительно![]() и
и![]() уравнения.
уравнения.
![]() ,
,
![]() .
.
После замены получим интегралы
![]() .
.
В первом из них
применим подстановку
![]() ,
во втором - подстановку
,
во втором - подстановку![]() .
.
Рассмотрим
соответствующие примеры. Первый случай
![]() :
:
![]()
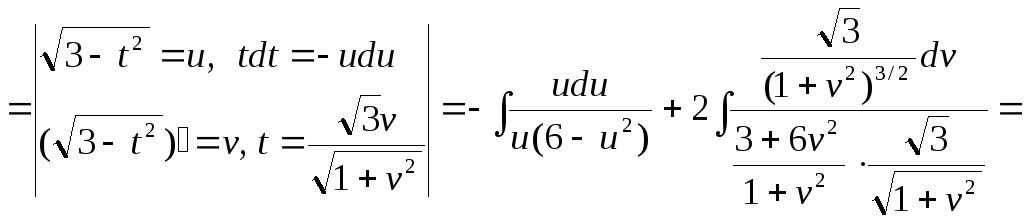
![]() .
.
Случай второй (![]() :
:
![]() .
.
Решаем систему
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
Делаем замену
![]() ,
,![]() ,
,![]() .
.
Дальше интеграл считается совершенно аналогично предыдущему.
Интеграл вида
![]() ,
,
![]() ,
,![]() ,
где
,
где![]() - рациональная функция, можно свести к
интегралу от рациональных функций
посредством одной изподстановок
Эйлера:
- рациональная функция, можно свести к
интегралу от рациональных функций
посредством одной изподстановок
Эйлера:
![]() ,
a>0,
,
a>0,
![]() ,
c>0,
,
c>0,
![]() ,
,
![]() ,
,
где
![]() один
из корней квадратного трехчлена
один
из корней квадратного трехчлена![]() .
.
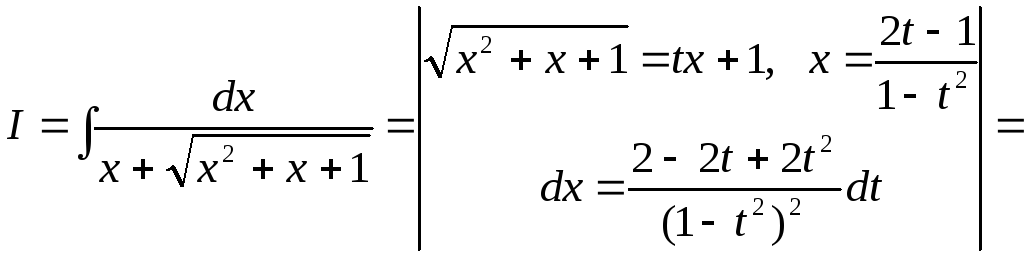
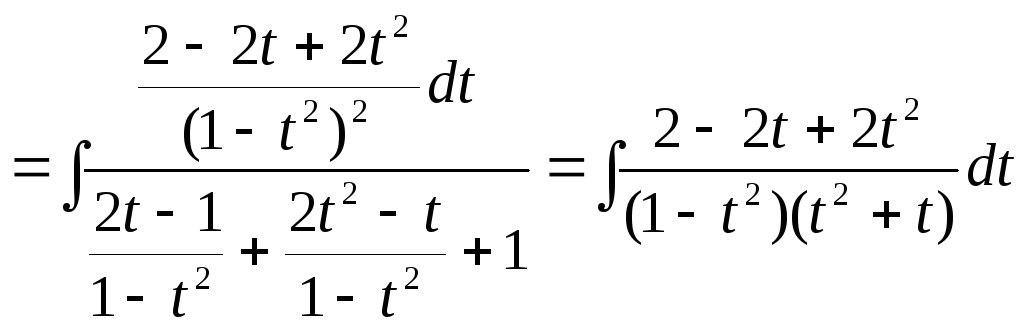 .
.
![]() .
.
![]() .
.
![]()
![]() .
.
![]()
![]()
![]() .
.
Упражнение. С помощью подстановки Эйлера вычислить соответствующие интегралы из расчетно-графической работы.
Интегралы вида
![]() ,
,
где
![]() ,
,![]() ,
причем
,
причем![]() ,
называютинтегралом от дифференциального
бинома. Данный интеграл сводится к
интегралу от рациональной функции в
следующих трех случаях:
,
называютинтегралом от дифференциального
бинома. Данный интеграл сводится к
интегралу от рациональной функции в
следующих трех случаях:
![]() - подстановкой
- подстановкой
![]() ,
где
,
где![]() - общий знаменательm
, n;
- общий знаменательm
, n;
![]() - подстановкой
- подстановкой
![]() ,
гдеq– знаменательр;
,
гдеq– знаменательр;
![]() - подстановкой
- подстановкой
![]() ,
гдеq– знаменательр.
,
гдеq– знаменательр.
Рассмотрим пример
![]() .
.
Здесь
![]() ,
,
![]() .
.![]() ,
,![]() ,
,![]() .
.
Делаем замену
![]() ,
,
![]() ,
,![]() .
.
Тогда
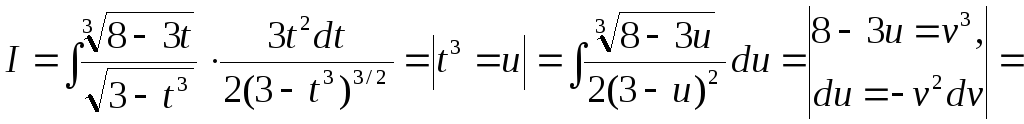
![]() .
.
Этот интеграл вычисляется также как интегралы в пп. 4, 5
Упражнение. Вычислить соответствующие интегралы от дифференциального бинома входящие в расчетно-графическую работу.
|
Найти неопределенные интегралы (в пунктах 1.1-1.5 результаты проверить дифференцированием) | ||||||
|
1.1 |
1.2 | |||||
|
10. |
11. |
|
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
|
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26. |
27.
28.
29.
30. | |
|
1.3 |
1.4 | |||
|
|
|
|
|
30.
|
|
1.5 |
1.6 | ||||
|
|
|
|
|
|
|
|
1.7 |
1.8 | ||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
|
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
|
25.
26.
27.
28.
29.
30.
|
|
1.9 |
1.10 | ||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
11 |
1.12 | ||||
|
|
|
|
|
|
|
|
1.13 |
1.14 | ||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10. |
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
2.1 |
2.2 | ||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
2.3 |
2.4 | ||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10. |
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
|
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
2.5 |
2.6 | ||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
2.7 |
2.8 | ||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
2.9 |
2.10 | |||||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
| |||
|
|
|
| ||||||
|
|
| |||||||
|
3.1 |
3.2 | ||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20. |
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
3.3 |
3.4 | ||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
3.5 |
3.6 | ||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
|
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
3.7 |
3.8 | ||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
4.1 | ||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
4.2 | ||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
4.3 | ||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
4.4 | ||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
|
|
4.5 |
4.6 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
| ||||||
|
4.7 |
4.8 |
| ||||||||||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|
| ||||||
|
4.9 | ||
|
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
|
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
|