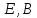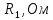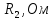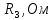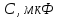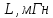Архив3 / kursach_OTTs (2) / курсач ОТЦ / Курсовой проект ТГТУ.210303.022 ДЭ / Текстовые документы ТГТУ.210303.022 ДЭ / Пояснительная записка ТГТУ.210303.022 ТЭ-ПЗ

СОДЕРЖАНИЕ

4

5

6

9

11

12

ВВЕДЕНИЕ ………………………………………………………………..………..

1 Расчет переходных процессов с применением классического метода …………

2 Расчет переходных процессов с применением операторного метода ………….

ЗАКЛЮЧЕНИЕ …………………………………………………………………….

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ ………………………………….

ВВЕДЕНИЕ

5

При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.

При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи.

Основные методы анализа переходных процессов в линейных цепях:

1. Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.

2. Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.

1 Расчет переходных процессов с применением классического метода

6

Для электрической цепи (рисунок 1) и исходных данных (таблица 1) найти закон изменения тока 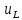при замыкании ключа К. В цепи действует постоянная ЭДС .

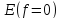Рисунок 1 – Схема электрическая принципиальная.

Таблица 1 – Исходные данные для проектирования

150	4	10	5	6	5	2

Рассчитаем начальные нулевые условия до коммутации.

Так как следовательно цепь разомкнута и все напряжение источника напряжения E падает на конденсаторе:

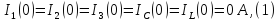
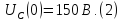
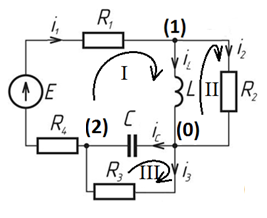
Рисунок 2 – Схема электрическая принципиальная после коммутации.

Рассчитаем начальные условия после коммутации.

Так как 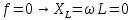, следовательно:

7

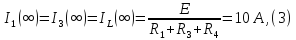
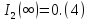
Так как 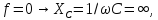следовательно:

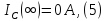
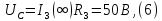
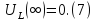
Закон изменения тока на индуктивности будет иметь вид:

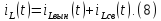
Для нахождения закона изменения тока на индуктивности при переходном процессе необходимо рассчитать входное сопротивление цепи относительно источника постоянной ЭДС (рисунок 2).

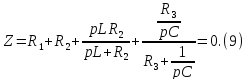
Преобразуем его:

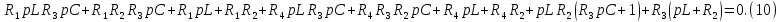
И в итоге получим:

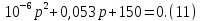
Решив это уравнение, получим корни:

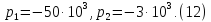
Так как корнями характеристического уравнения являются отрицательные числа, то закон изменения тока на индуктивности будет иметь вид экспоненциального затухания:

8

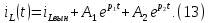
Составим систему уравнений по законам Кирхгофа:

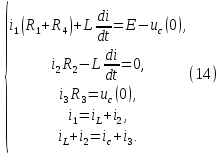
Так как все токи все токи в начальный момент времени равны нулю, то:

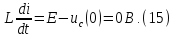
Используя нулевые начальные условия и условия, рассчитаем константы интегрирования :

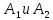Откуда:

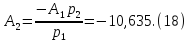
Следовательно, закон изменения напряжения на индуктивности имеет вид

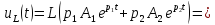
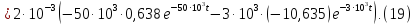
9

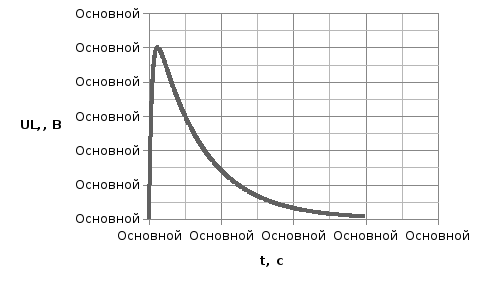
Рисунок 3 – Закон изменения напряжения 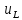, рассчитанный классическим методом.

2 Расчет переходных процессов с применением операторного метода

9

Рассчитаем закон изменения напряжения 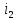операторным методом. В решении будем использовать найденные по классическому методу корни характеристического уравнения , нулевые начальные условия и условия после коммутации.

Рисунок 4 – Схема электрическая принципиальная послекоммутационная

Для нахождения закона изменения напряжения 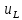составим систему линейных уравнений по методу узловых напряжений:

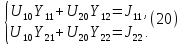
Выразим коэффициенты данной системы уравнений:

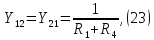
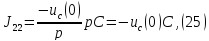
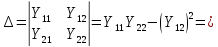
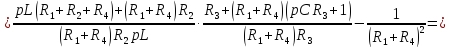
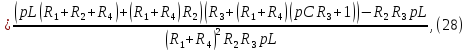
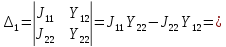
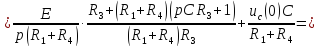
Подставим числовые значения:

Рисунок 5 – Закон изменения тока 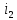, рассчитанный операторным методом

ЗАКЛЮЧЕНИЕ

11

В данном курсовом проекте были рассмотрены различные методы расчета переходных процессов в линейных электрических цепях. На основе исходных данных для проектирования (рисунок 1, таблица 1) в данном курсовом проекте был рассчитан закон изменения тока 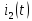классическим и операторным методами. Полученные результаты (рисунок 3, 5) не имеют значимых погрешностей, что говорит о возможности использования любого из рассмотренных методов для расчета переходных процессов в линейных электрических цепях.

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

12

1. Пудовкин, А.П. Основы теории цепей. Учебное пособие по основам теории цепей / А.П. Пудовкин и [др] – Издательство ТГТУ, 2008 – 90 с.

2. Попов, В.П. Основы теории цепей. Учебник для вузов / В.П. Попов – М.: Высшая школа, 2008 – 575 с.

3. Бессонов, Л.А. Линейные электрические цепи / Л.А. Бессонов – М.: Высшая школа, 1983 – 336 с.

4. Бирюков, В.Н. Сборник задач по теории цепей / В.Н. Бирюков и [др] – М.: Высшая школа, 1985 – 239 с.

5. Лосев, А.К. Теория линейных электрических цепей / А.К. Лосев – М.: Высшая школа, 1987 – 512 с.

6. Шебес, М.Р. Задачник по теории линейных электрических цепей / М.Р. Шебес – М.: Высшая школа, 1990 – 488с.

ТГТУ.210303.022 ПЗ

Изм.

Лист

№ Документа

Подпись

Дата

Разработал

Шибин В.А.

Переходные процессы в линейных электрических цепях Пояснительная записка

Лит.

Лист

Листов

Проверил

Пудовкин А.П.

1

9

Рецензиров.

РТ гр. СРБ – 31

Н. контр.

Утвердил

Пудовкин А.П.