2. Примеры задач и их решения

Пример 1. При 25 °С осмотическое давление раствора, содержащего 2,8 г высокомолекулярного соединения (ВМС) в 200 мл раствора, равно 0,7 кПа. Найти молекулярную массу растворённого вещества.

Решение. Из формулы (1) следует, что

где R = 8,314 Дж/(моль∙К), а Т = t + 273 ° = 25 °+ 273 °= 298 К. Подставим в это уравнение данные из условия

приведем единицы измерений в соответствие и определим молекулярную массу ВМС

отсюда молекулярная масса ВМС равна 4,95-10⁴ у.е.

Ответ: 4,95-10⁴.

Пример 2. В 1 мл раствора содержится 10¹⁸ молекул неэлектролита. Вычислить осмотическое давление этого раствора при 25 °С в атмосферах.

Решение. Поскольку 1 мл раствора содержит 10¹⁸ молекул неэлектролита, то в 1 л его находится молекул этого вещества.Следовательно, молярная концентрация данного раствора равна

По уравнению (1) вычислим осмотическое давление предложенного раствора

π = С_МRT =1,66 ∙10^-3∙0,082∙298 = 0,041 атм.

R=0,082 л∙атм/моль∙град и T= t+273⁰=25⁰+273⁰=298K.

Ответ: 0,041 атм.

Пример 3. Кажущаяся степень диссоциации хлорида цинка ZnCl₂ в 0,1 н растворе равна 0,85. Чему равно осмотическое давление этого раствора при 17°С в мм.рт.ст., атм., кПа?

Решение. ZnCl₂ - сильный электролит, при растворении в воде полностью диссоциирует ZnCl→ Zn²⁺ + 2Сl^-. Поскольку молекула ZnCl₂ распадается на три иона, то n = 3.

Осмотическое давление этого раствора определим по формуле (10): π = i С_МRT

Молярность раствора вычислим по формуле С_м ∙ М = С_н ∙Э или

но так как для хлорида цинка М = 2Э, тогда

Изотонический коэффициент рассчитаем по уравнению (6):

i= α' (n-1) +1 =0,85(3-1)+ 1 =2,7.

R = 62,36 л ∙мм рт.ст/ (моль∙град),

Т = t +273° = 17° + 273° = 290 К.

Тогда π =2,7∙0,05∙62,36∙290= 2441,1 мм. рт. ст.= 3,21 атм. = 325,5кПа.

Ответы: 2441,1 мм. рт. ст., 3,21 атм., 325,5кПа.

Пример 4. Чему равно давление насыщенного пара над 10%-ным раствором карбамида СО(NН₂)₂ при 100 ⁰С?

Решение. В 100 г 10 %-го раствора содержится 10г карбамида и 90г воды. Далее в решении используем уравнение (2), т.е.

, тогда Р°- Р = Р°- N_B и далее

Р = Р°- Р°∙ N_B = P°(1-N_B).

Из этого соотношения и уравнения (2) для нашего расчёта выводим формулу:

где Р° = 101,32 кПа - давление насыщенного пара над водой при 100°С [5, табл. 16];

m= 10 г;М= 60 г/моль;m= 90 г/моль;М= 18 г/моль,

тогда .

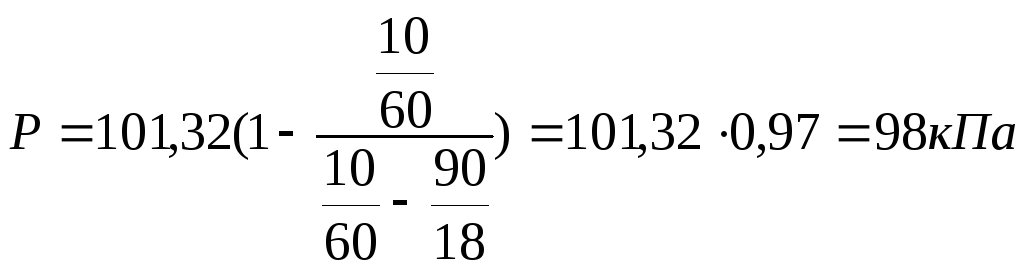Ответ: 98 кПа.

Пример 5. При 100 °С давление пара раствора, содержащего 0,05 моль сульфата натрия Na₂SO₄ в 450 г воды, равно 100,8 кПа. Определить кажущуюся степень диссоциации Na₂SO₄ в этом растворе.

Решение. Кажущуюся степень диссоциации соли в этом растворе найдем по уравнению (7), т.е.

Изотонический коэффициент i найдем по уравнению

, Р по условию равно 100,8 кПа, а Р° возьмём из [5,табл.16,],

тогда ∆Р_оп = 101,32 - 100,8 = 0,52кПа.

∆Р_выч рассчитаем по уравнению (2): ,

где n_в=0,05 моль Na₂SO₄, а n_р-ля=450/18=25 моль Н₂О, тогда

и .

При диссоциации соли Na₂SO₄=2Na⁺+SO₄^2- молекула Na₂SO₄ распадается на три иона, поэтому n=3.

Подставляя найденные значения i и n в уравнение (7), определим

кажущуюся степень диссоциации Na₂SO₄:

.

Ответ: 0,8 (80 %) .

Пример 6. При какой приблизительно температуре будет кипеть 50 %-й (по массе) раствор сахарозы C₁₁H₂₂O₁₁?

Решение. Температуру кипения этого раствора определим по формуле ∆t_k=t_{k р-ра}- t_{k р-ля} или t_{k р-ра}= t_{k р-ля}+∆t,

где - t_{k р-ля} (Н₂О)=100⁰С. Поскольку C₁₁H₂₂O₁₁- неэлектролит, то ∆t_k найдем по формуле (3), т.е.

где растворителем является вода, а Е= 0,52°; раствор 50 %-й -это значит, что в 100 г его содержится 50 г сахарозы и 50 г воды, т.е.

m_в = 50 г и m_р-ля= 50 г; М_в= 342 г/моль - молярная масса сахарозы,

тогда иt_{k р-ра}= 100⁰ + 1,52⁰=101,52⁰С.

Ответ: 101,52С.

Пример 7. При какой температуре закипит 2,12М водный раствор СаСl₂? Плотность этого раствора равна 1,177г/мл. Кажущуюся степень диссоциации соли в этом растворе принять равной 90%.

Решение. Температуру кипения 2,12М раствора СаСl₂ определим по формуле ∆t_k=t_{k р-ра}- t_{k р-ля} или t_{k р-ра}= t_{k р-ля}+∆t,

где - t_{k р-ля} (Н₂О)=100⁰С.

СаСl₂ - электролит, поэтому ∆t_k раствора вычислим по уравнению (2):

Для расчета изотонического коэффициента i используем уравнение i=α^/(n-1)+1.

Хлорид кальция в воде полностью диссоциирует.

СаСl₂ = Са²⁺ + 2Сl^-, т.е. из одной молекулы СаСl₂ образуются один ион Са²⁺ и два иона 2Сl^-, поэтому n=1+2=3,

тогда i=0,9∙(3-1)+1=2,8

Е = Е - эбуллиоскопическая константа воды [5 табл.5].

М_в =М_СаСl2=111 г/моль молярная масса хлорида кальция.

М_в и m_р-ля найдём, используя приведенные в условии примера См = 2,12 моль/л и плотность раствора, равную 1,177 г/мл. Сначала определим массу 1 л этого раствора

m_р-ра=ρ∙V_р-ра= 1,177г/мл ∙ 1000мл = 1177 г .

m_в-ва=m=M∙n=111∙2,12=235,32 г,

где n=2,12 - количество молей СаСl₂ в 1 л растворе.

m_р-ля= m=m_р-ра-m=1177-235,32=941,68г.

Тогда и=103,3°C

Ответ: 103,3С.

Пример 8. В каком массовом отношении нужно смешать этиленгликоль (двухатомный спирт) С₂Н₆О₂ с водой, чтобы получился антифриз (жидкость, замерзающая при низких температурах), замерзающий при - 30 °С?

Решение. Из формулы (4) следует

где ;

М_спирта= 62 г/моль - молярная масса этиленгликодя;

К = 1,86 °- криоскопическая константа воды [5],

тогда

т.е., например, антифриз, изготовленный из 10 кг воды и 10 кг этиленгликоля, замерзнет при - 30 °С.

Ответ:

Пример 9. 10 %-й раствор A1₂(SO₄)₃ замерзает при - 2,7 °С. Определить кажущуюся степень диссоциации этой соли в предложенном растворе.

Решение. Используем формулу (7), т.е. .

Из уравнения (13) имеем

где

М_в=342 г/моль - молярная масса Al₂(SO₄)₃;

К- криоскопическая константа воды [5];

по условию задачи имеем 10%-й раствор Al₂(SO₄)₃ - это значит, что m_в=10г сульфата алюминия и m_р-ля=90г воды, тогда

Al₂(SO₄)₃ - сильный электролит, при его диссоциации

Al₂(SO₄)₃= 2Al³⁺+3SO₄^2- из одной молекулы соли образуется 2 катиона Al³⁺+ и 3 аниона SO₄^2-, т.е. n=2+3=5.

И наконец, (87%).

Ответ: 0,87 (87%).

Пример 10. рН 0,01 М раствора муравьиной кислоты НСООН равен 2,88. Вычислить степень и константу диссоциации кислоты в этом растворе.

Решение. Степень диссоциации НСООН в 0,01 М растворе определим по уравнению (8), т.е.

НСООН - электролит слабый, поэтому диссоциирует частично и обра­тимо по уравнению

НСООН↔НСОО^- +Н⁺.

Константа её диссоциации К_Д выражается отношением

,

а так как из уравнения (5) следует, что и

, тогда ,

но и(электролит слабый), отсюда

найдем по уравнению илии тогда,

и

Ответ: 0,132; 1,74∙10^-4.