Общая химия (АиАХ, ПТМ, ПТЭ, РС, МиТЭ) / методические указания / термодинамика

3. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ

Работа выполняется звеньями из 2-3 студентов.

Опыт №1. Определение теплоты нейтрализации.

Упрощенный калориметр состоит из двух стаканов. В большой стеклянный стакан вставьте другой стакан меньшего размера. Они не должны между собой соприкасаться. Во избежание потерь теплоты через стенки внутреннего калориметрического стакана между ними поместите прокладки. Внутренний стакан закройте крышкой с тремя отверстиями.

Взвесьте внутренний калориметрический стакан на весах и налейте в него 100 мл раствора щелочи; отметьте температуру раствора с точностью до 0,1⁰С (t_щ). Вставьте внутренний стакан с раствором щелочи во внешний стакан, закройте его крышкой. В отверстия крышки поместите мешалку, термометр, воронку. Отмерьте цилиндром 100 мл раствора кислоты и измерьте его температуру (t_к).

При непрерывном помешивании быстро прилейте через воронку раствор кислоты к раствору щелочи. Отметьте самую высокую температуру раствора – t_кон, которую показывает термометр после смешения растворов. Вычислите среднюю температуру растворов до реакции – t_нач (среднее арифметическое из температур растворов кислот и щелочи), затем рассчитайте разницу

∆ t = t_кон - t_нач.

Вычислите теплоту q, выделяющуюся в калориметре, по формуле

q= ∆ t∙c_m,

где c_m- теплоемкость системы.

Теплоемкость системы

c_m= с₁m₁+ c₂m₂,

где с₁ – удельная теплоемкость стекла, которая равна 0,753 Дж/(г∙град); m₁ – масса калориметрического стакана; с₂ – удельная теплоемкость раствора, которую принимают равной 4,184 Дж/(г∙град); m₂ – масса раствора.

Масса раствора

m₂= V_kρ_k+V_щρ_щ,

где V_k – объем кислоты; ρ_k – плотность кислоты; V_щ – объем щелочи; ρ_щ – плотность щелочи.

Тепловой эффект реакции нейтрализации (Дж/моль) рассчитайте по формуле

∆Н= .

Определение проведите по 2 раза с сильными кислотами и щелочами и один раз со слабыми.

Результаты опытов запишите в таблицу.

Система	m1, г	m2, г	tщ и tк	tнач= (tщ+tк)/2	tкон	∆ t	q, кДж	∆Н, кДж/моль
I. NaOH, HCl
II. KOH, HNO3
III.NH4OH, CH3COOH

Сравните полученные данные ∆Н с истинным значением теплоты нейтрализации, равной 56,9 кДж/моль, найдите отклонения результатов от истинного значения теплоты нейтрализации сильной кислоты сильным основанием.

Опыт №2. Определение теплоты гидратации.

При растворении кристаллических солей в воде происходят два основных процесса: первый – эндотермический, связанный с разрушением кристаллической решетки; второй – экзотермический, обусловленный взаимодействием частиц растворяемого вещества с молекулами растворителя и образованием гидратированных частиц (ионов, молекул). В зависимости от того, какой из двух процессов преобладает, тепловой эффект растворения может быть положительным или отрицательным.

В предварительно взвешенный калориметрический стакан налейте 150 мл дистиллированной воды. Отвесьте 8 г безводного сульфата меди с точностью до 0,01 г. Отметьте с точностью до 0,1⁰температуру воды в калориметре - t_нач, затем при перемешивании внесите соль в воду и отметьте максимальную температуру - t_кон.

Рассчитайте количество теплоты, выделяющееся в калориметре, по формуле

q= [с₁m_ст+ c₂ (m_в + m_с)]∆t,

где q – количество выделившейся теплоты, Дж; с₁- удельная теплоемкость стекла [0,753 Дж/(г∙град)]; m_ст – масса калориметрического стакана, г; с₂ – удельная теплоемкость раствора [4,184 Дж/(г∙град)]; m_в – масса воды, г; m_с - масса соли, г; ∆t – разность температур.

Рассчитайте тепловой эффект ∆Н по формуле

∆Н=

где М – молярная масса безводной соли.

Теплота растворения CuSO₄∙5H₂O при 20⁰С ∆Н_р=11,5 кДж/моль.

Рассчитайте теплоту гидратации сульфата меди:

CuSO_4(к) + 5H₂O_(ж)= CuSO₄∙5H₂O_(к).

Согласно закону Гесса,

∆Н_гидр= ∆Н- ∆Н_р.

Полученные результаты занесите в таблицу.

mст, г	mв, г	mс, г	tнач	tкон	∆t= tкон - tнач	q, Дж	∆Нгидр, кДж/моль

4. ПРИМЕРЫ РАСЧЕТОВ

ПРИМЕР 1. По термохимическому уравнению рассчитать стандартную энтальпию образования продукта реакции:

2Fe₃O_4(T) + 9SO_2(Г) + 5О_2(Г) = 3Fe₂(SO₄)_3(T), ∆Н⁰_298(р)=-2845,7 кДж.

РЕШЕНИЕ. Согласно первому следствию из закона Гесса, стандартная энтальпия данной реакции

следовательно, стандартная энтальпия образования 3Fe₂(SO₄)_3(Т)

ПРИМЕР 2. Рассчитайте тепловой эффект реакции горения сероводорода Н₂S_(г)+3/2O₂ →H₂O_(ж) + SO_2(г) по следующим данным:

1) S_(к) + Н₂ → Н₂S_(г), ∆Н₁= -20,17 кДж,

2) Н₂ + 1/2О₂ →Н₂О_(ж), ∆Н₂= -286,0 кДж,

3) S_(к) + О₂ → SО_2(г), ∆Н₃ = -297,0 кДж.

РЕШЕНИЕ. Уравнения 1-3 – это термохимические уравнения образования соответственно 1 моль Н₂S_(г), Н₂О_(ж), SО_2(г) из простых веществ в стандартных условиях.

Если сложить термохимические уравнения 2 и 3 и вычесть уравнение 1, получим искомое уравнение

+ Н₂ + 1/2О₂ →Н₂О_(ж), ∆Н₁

+ S_(к) + О₂ → SО_2(г), ∆Н₂

- S_(к) + Н₂ → Н₂S_(г), ∆Н₃

Н₂S_(г)+ 3/2O₂ →H₂O_(ж) + SO_2(г), ∆Н=∆Н₁+∆Н₂-∆Н₃.

Подставив численное значение энтальпий образования Н₂S_(г), Н₂О_(ж), SО_2(г), получим значение теплового эффекта реакции

∆Н= -286 – 297 – (- 20,17) = -562,8 кДж.

ПРИМЕР 3. С помощью термохимического уравнения Н₂S_(г)+3/2O₂ →H₂O_(ж) + SO_2(г) + 562,8 кДж определите объем сгоревшего сероводорода, если известно, что в результате реакции выделилось 281,4 кДж.

РЕШЕНИЕ. Проведем расчет по уравнению и определим объем сероводорода:

_{х л 281,4 кДж}

Н₂S_(г)+3/2O₂ →H₂O_(ж) + SO_2(г) + 562,8 кДж

^{22,4 л}

22,4 562,8 кДж

х = 281,4 кДж ; х= V(Н₂S) = 11,2 л.

ПРИМЕР 4. Рассчитайте стандартную энергию Гиббса реакции 2Н₂S_(г)+ 3O_{2 (г)}→2H₂O_(ж) +2 SO_2(г). Является ли эта реакция термодинамически возможной в закрытой системе?

РЕШЕНИЕ. Стандартную энергию Гиббса данной реакции рассчитывают по уравнению Гиббса-Гельмгольца

∆G⁰_298(р) =∆H⁰_298(р) – 298 ∆S⁰_298(р),

где стандартная энтальпия реакции

Стандартная энтропия реакции

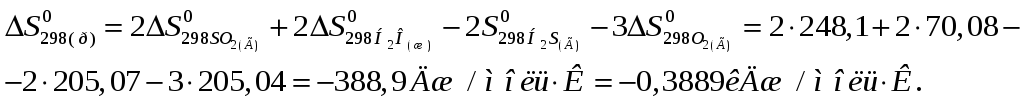
Подставляя числовые значения стандартных энтальпии и энтропии процесса в уравнение Гиббса-Гельмгольца, получаем

∆G⁰_298(р)= -1123,46 – 298 (-0,3889) = -1007,6 кДж (∆G⁰_298(р)<0),

Следовательно, данная реакция является термодинамически возможной в закрытой системе при стандартных условиях.