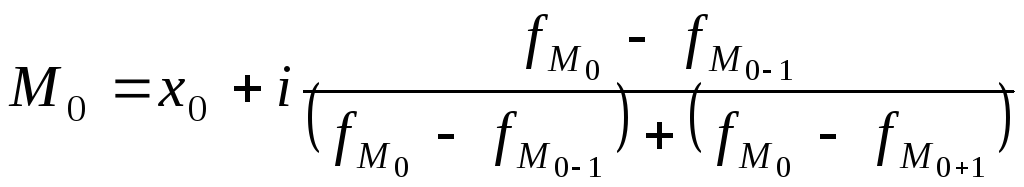Степенные средние величины

Название средней величины	Показатель степени	Формула расчета
		простая	взвешенная
Гармоническая	-1
Геометрическая	0
Арифметическая	1
Квадратическая	2
Кубическая	3

Структурные средние величины

Название средней величины	Формула расчета
Мода интервального ряда распределения
Медиана интервального ряда распределения

Условные обозначения

x_i – значение признака;

f_i – частота повторения признака в совокупности;

n – число единиц совокупности;

сложный вес; ;

х₀ - нижняя граница модального (медианного) интервала;

i - величина модального (медианного) интервала;

- частота модального интервала;

- частота интервала, предшествующего модальному;

-частота интервала, следующего за модальным;

- сумма частот;

- сумма наблюдений, накопленная до начала медианного интервала;

- частота медианного интервала.

Тема 6. Вариационный анализ

Понятие вариации. Задачи статистического изучения вариации. Абсолютные и относительные показатели вариации, их практическое применение.

Тема 7. Выборочный метод

Выборочное наблюдение и его значение. Генеральная и выборочная совокупности. Способы отбора единиц в выборочную совокупность. Ошибки выборки, их классификация. Повторный и бесповторный отбор. Определение необходимой численности выборки. Способы распространения данных выборочного наблюдения на генеральную совокупность.

Основные формулы

Выборочные средние и относительные величины распространяются на генеральную совокупность с учетом предела их возможной ошибки.

_x – предельная ошибка выборки для среднего значения (_x=t);

_p – предельная ошибка выборки для доли (_p=t).

Величина возможного предела (доверительного интервала):

Формулы средней ошибки простой случайной выборки

Средняя ошибка,	Способ отбора единиц
	повторный	бесповторный
Для средней
Для доли

Формулы для определения численности простой случайной выборки

Численность выборки	Способ отбора единиц
	повторный	бесповторный
Для средней
Для доли

Условные обозначения

N– численность генеральной совокупности;

n – численность выборочной совокупности;

- выборочная средняя;

w – выборочная доля; w=m/n, где m – число единиц, обладающих изучаемым признаком в выборочной совокупности;

- выборочная дисперсия (дисперсия признака в выборочной совокупности);

t – коэффициент доверия по распределению Стъюдента (при вероятности 0,954 t=2; при вероятности 0,997 t=3).

Тема 8. Статистическое изучение динамики общественных и экономических явлений

Понятие и основные правила построения рядов динамики. Смыкание рядов динамики. Виды рядов динамики и особенности их анализа. Абсолютные, относительные и средние показатели рядов динамики. Методика расчета цепных и базисных показателей в рядах динамики. Структура ряда динамики. Тренд и способы его выявления. Изучение и измерение сезонных колебаний. Интерполяция и экстраполяция рядов динамики.

Основные формулы

Абсолютные и относительные показатели динамики
Показатель	Цепной	Базисный
Абсолютный прирост	=Yi-Yi-1	=Yi-Y0
Коэффициент роста	Kp=Yi/Yi-1	Kp=Yi/Y0
Темп роста	Tp=Kp100	Tp=Kp100
Темп прироста	Tn=(Kp-1)100 Tn=Tp-100 Tn=(/yi-1)100	Tn=(Kp-1)100 Tn=Tp-100 Tn=(/y0)100
Абсолютное значение 1% прироста	A=/Tn A=Yi-1/100	A=/Tn A=Y0/100
Средние показатели динамики

Наименование показателя	Метод расчета
Средний уровень ряда динамики В моментном ряду: с равностоящими уровнями
с неравностоящими уровнями

Наименование показателя	Метод расчета
В интервальном ряду: с равностоящими уровнями
с неравностоящими уровнями
Средний абсолютный прирост
Средний коэффициент роста
Средний темп роста
Средний темп прироста
Средняя величина абсолютного значения 1% прироста

Условные обозначения

Y₀, – начальный, текущий и конечный уровни ряда динамики;

- длительность интервала времени между уровнями;

n – общее число уровней ряда динамики.