6. Найти точное решение краевой задачи:
а)
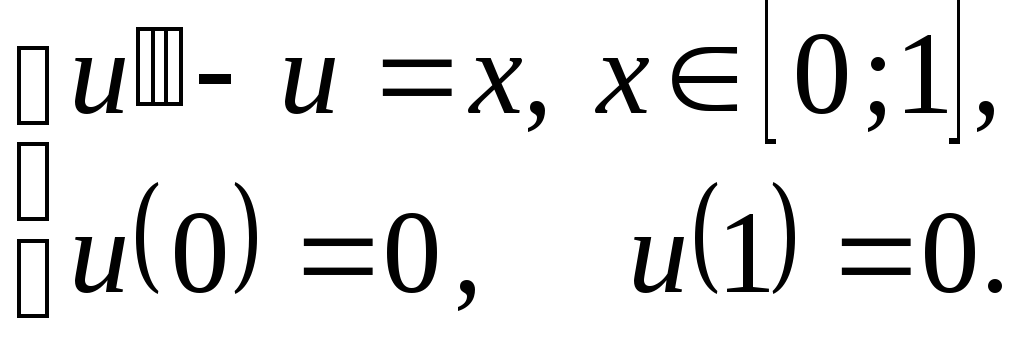;б)
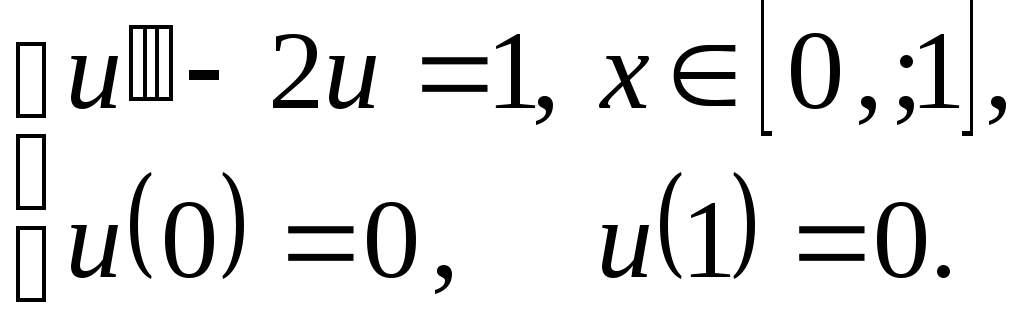
7. Дана краевая задача:
,
,
,
.
Будем считать, что
у нас есть программа для вычисления
приближенного решения этой краевой
задачи разностным методом при заданном
значении числа отрезков разбиения N.
Опишите, каким образом можно подобрать
значение N
так, чтобы погрешность приближенного
решения этой задачи, полученного с
помощью этой программы, не превышала
заданного положительного числа
?
Список использованной и рекомендуемой литературы
Основная литература
Трубников, С.В. Вычислительная математика: учебное пособие / С.В. Трубников, Б.В. Порошин. – Брянск: БГТУ, 2005.
Дополнительная литература
Бахвалов, Н.С., Численные методы / Н.Г.Бахвалов. – М.: Наука, 1987.
Вержбицкий, В.М. Основы численных методов: учебник для вузов / В.М.Вержбицкий. – М.:Высш. шк., 2002.
Калиткин, Н. Н. Численные методы / Н.Н.Калиткин. – М.: Наука, 1978.
Крылов, В.И. Вычислительные методы: В 2 Т. / В.И.Крылов [и др.]. – М.: Наука, 1976.
Рябенький, В. С. Введение в вычислительную математику / В.С.Рябенький. – М.: Наука, 1994.
Самарский, А.А. Численные методы: учеб. пособие для вузов / А.А.Самарский, А.В. Гулин. – М.: Наука, 1989.
Сборник задач по методам вычислений: учеб. пособие для вузов / под ред. П.И. Монастырного. – М.: Физматгиз, 1994.
Учебное издание
СЕРГЕЙ ВЛАДИМИРОВИЧ ТРУБНИКОВ
ЧИСЛЕННЫЕ МЕТОДЫ
Редактор издательства Т.И. Королева
Компьютерный набор С.В. Трубников
М.В. Березина
Темплан 2008г., п.10
Подписано в печать . .08. Формат 60х84 1/16 Бумага офсетная.
Офсетная печать. Усл.печ.л. 4,18. Уч.-изд.л. 4,18. Тираж 140 экз. Заказ
Издательство Брянского государственного технического университета
241035, г. Брянск, бульвар им. 50-летия Октября, 7, тел. 58-82-49
Лаборатория оперативной полиграфии БГТУ, ул. Институтская, 16