3. Задание №3. Решение системы линейных уравнений

1. Условие задания

Решить систему линейных уравнений

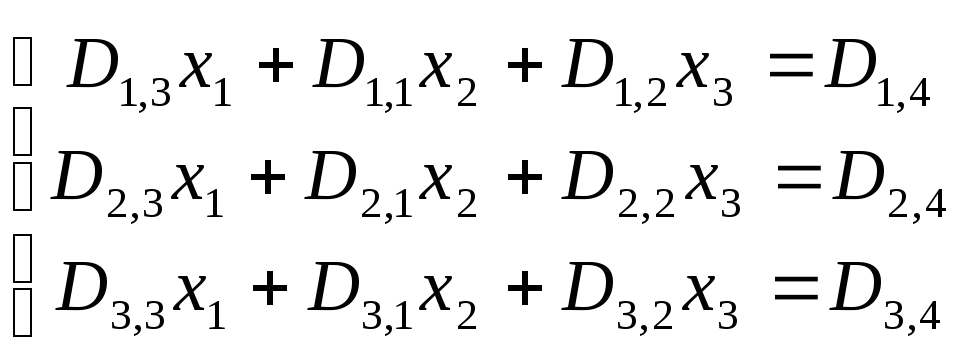
2. Решение

Решим полученную систему уравнений в Excel с применением последовательности операций линейной алгебры, а именно – с применением обратной матрицы (рис. 9). В результате получили вектор решения:

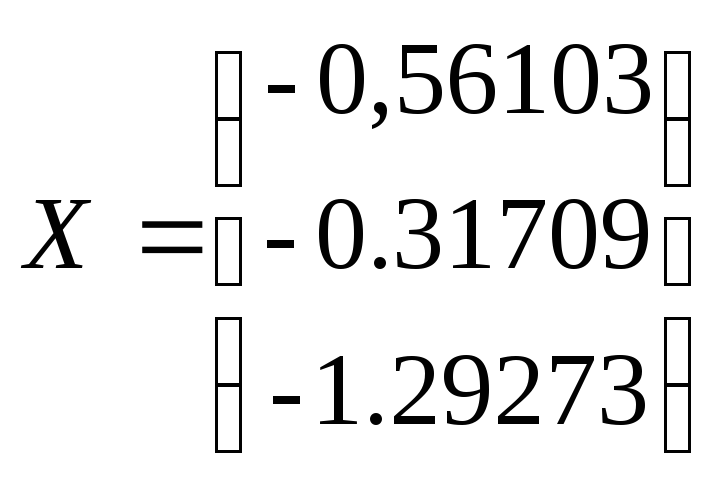
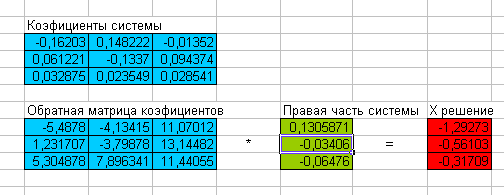
Рис. 9. Решение системы линейных уравнений с помощью Excel

3. Задание №4. Приближение таблично заданной функции

   1. Условие задания

Дана таблично заданная функция – пары точек , для которых необходимо выполнить следующее:

x	0.01	1	2	3	4	5	6	7	8	9
y	9.34	-5.15	-7.21	-7.99	-10.36	-11.2	-10.64	-10.54	-11.23	-12.89

• С помощью программы Mathcad провести кусочно-линейную интерполяцию и найти значения y для следующих значений x: 1.3, 2.6, 2.9, 3.3, 3.7, 4.2. Построить график.

• С помощью программы Mathcad провести полиномиальную интерполяцию и найти значения y для следующих значений x: 1.3, 2.6, 2.9, 3.3, 3.7, 4.2. Построить график. Записать уравнение полинома.

• Построить 2 вида аппроксимации: линейную и логарифмическую. Построить оба графика в одной координатной плоскости. В обоих случаях определить сумму квадратов отклонений для узловых точек. Данное задание выполнить как в Excel, так и в Mathcad.

3. Решение

1. Проведём кусочно-линейчатую интерполяцию для заданных точек 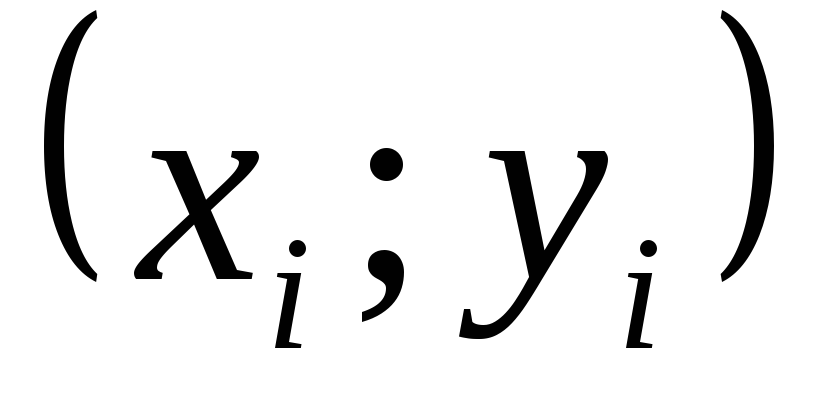и определяем значение функции для указанных значений аргумента (рис.10).

Таблица 1

x	1.3	2.6	2.9	3.3	3.7	4.2
y	-5.768	-7.678	-7.912	-8.701	-9.649	-10.528

2. Проведём полиномиальную интерполяцию. Учитывая, что задано 10 точек, то полином должен быть 9-й степени. В результате, получили полином, представленный на рис. 11. Построим его график, на котором отметим его исходные точки (рис. 11). По графику можно убедиться, что полином проходит через все точки.

3. С помощью полученного полинома определим для заданных точек значения функции (рис. 11).

Таблица 2

x	1.3	2.6	2.9	3.3	3.7	4.2
y	-6.655	-7.361	-7.794	-8.685	-9.694	-10.711

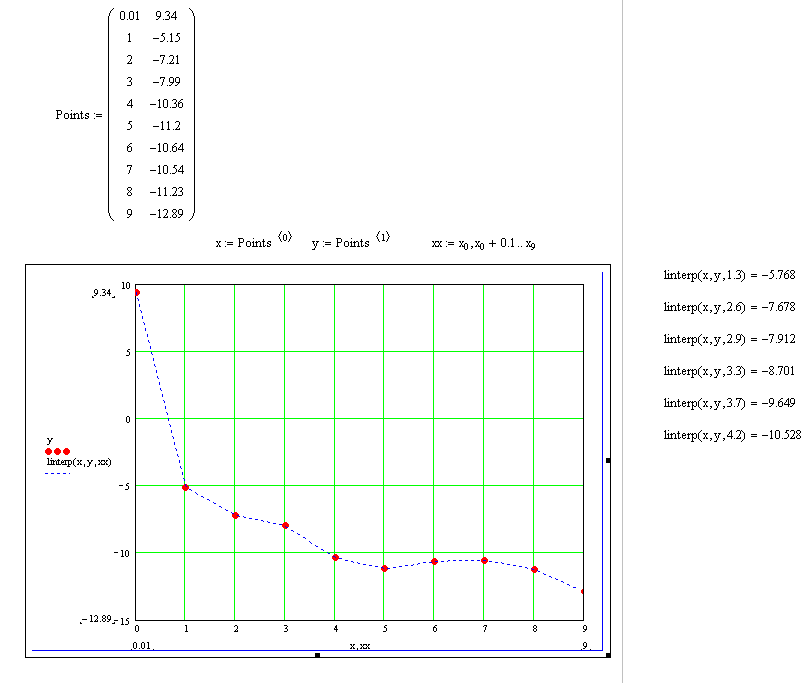
Рис. 10. Кусочно-линейная интерполяция в Mathcad.

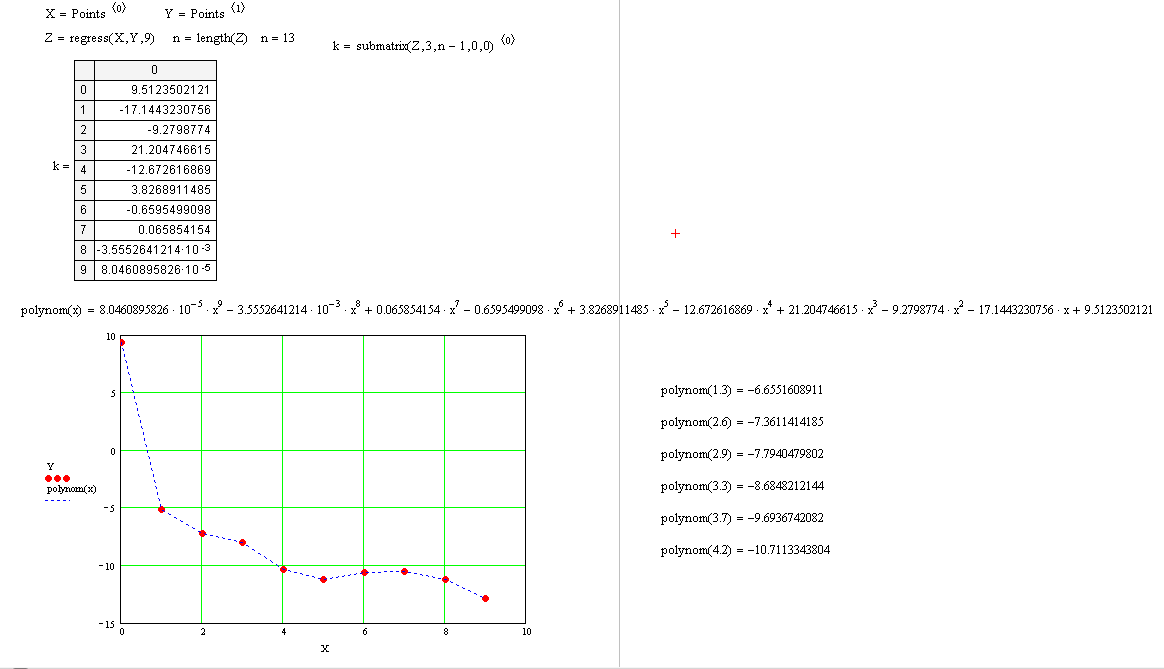
Рис. 11. Полиномиальная интерполяция в Mathcad.

4. Проведём с помощью Mathcad аппроксимацию для заданных точек с помощью линейной и логарифмической функции (рис. 12). Определим сумму квадратов отклонений для узловых точек (рис. 12):

• Для линейной функции эта величина равна 145,219.

• Для полинома 3-й степени эта величина равна 2.652

Можно сделать вывод, что с помощью логарифмической функции мы получаем более точное приближение.

Рис. 12. Аппроксимация точек в Mathcad.

5. Построим на одной координатной плоскости графики аппроксимирующих функций (рис. 13).

6. Проведем аппроксимацию точек с помощью Excel. Для этого сначала заполним исходную таблицу точек и отметим эти точки на координатной плоскости (рис. 14).

7. Вызовем контекстное меню для одной из точек на графики и выберем пункт «Добавить линию тренда…». Для начала проведем аппроксимацию с помощью логарифмической функции. Для этого в открывшемся диалоговом окне «Линия тренда» выберем «логарифмическая» (рис. 15).

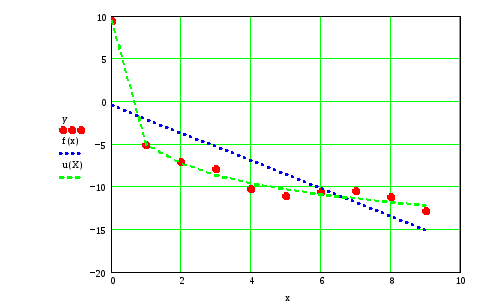
Рис. 13. Графики аппроксимирующихфункций.

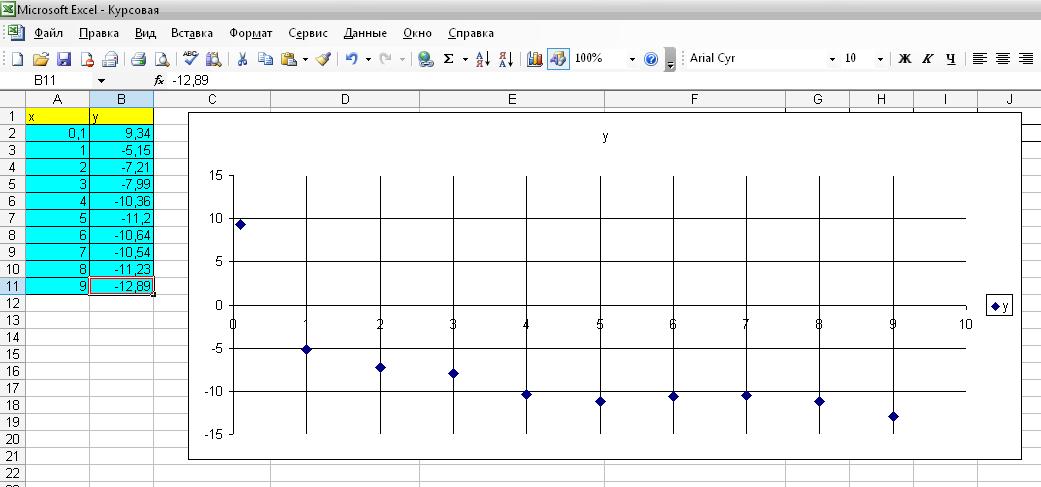
Рис. 14. Исходные точки для аппроксимации на координатной плоскости.

8. Аналогично добавил линию тренда на основе линейной функции. В настройках линий тренда выставим галочку «показывать уравнение на диаграмме». Получили следующие аппроксимирующие функции.

• Для линейной функции:

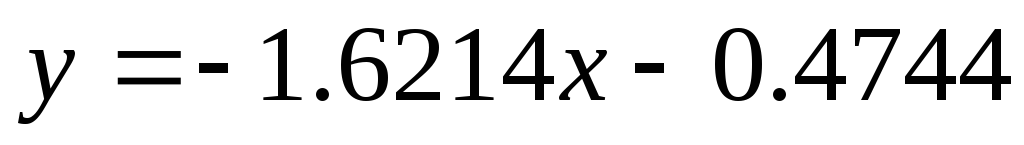
• Для логарифмической функции:

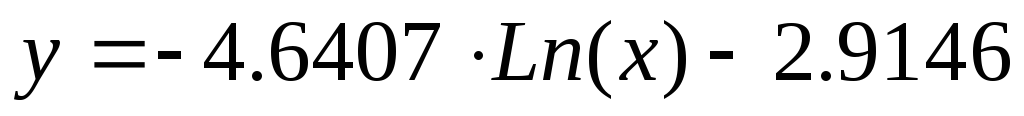
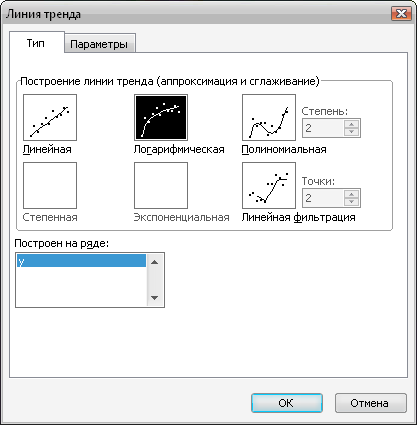
Рис. 15. Добавление на график аппроксимирующей линии (линии тренда).

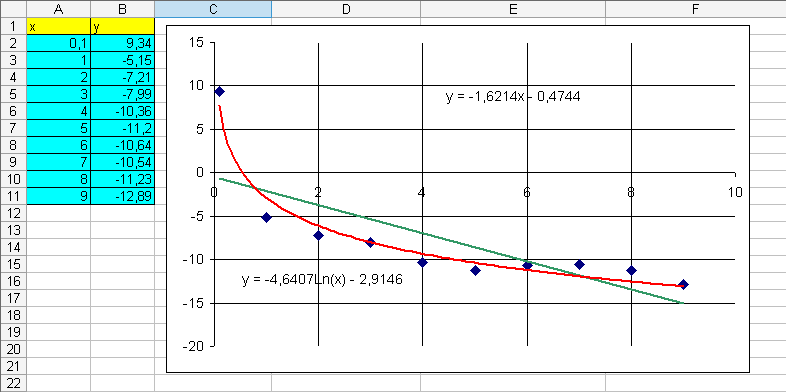
Рис. 16. Получение графиков функций аппроксимации.

9. Определим сумму квадратов отклонений для полученных

функций в узловых точках (рис. 17). Получим:

• Для линейной функции величина равна 157,9946536

• Для полинома 3-йстепени величина равна 16,916

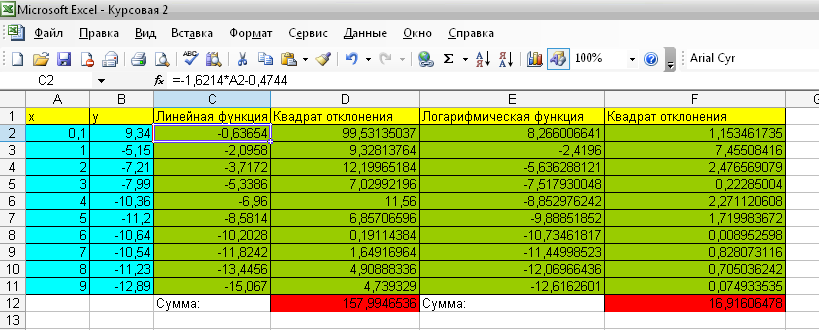
Рис. 17. Расчёт в Excel Суммы квадратов отклонений для аппроксимирующих функций.