
Практическая работа - матрицы и определители
.doc
1. Операции над матрицами
1.1. Найдите
линейную комбинацию
![]() матриц
матриц
![]() и
и
![]() .
.
1.2. Вычислите
матрицу
![]() ,
где
,
где
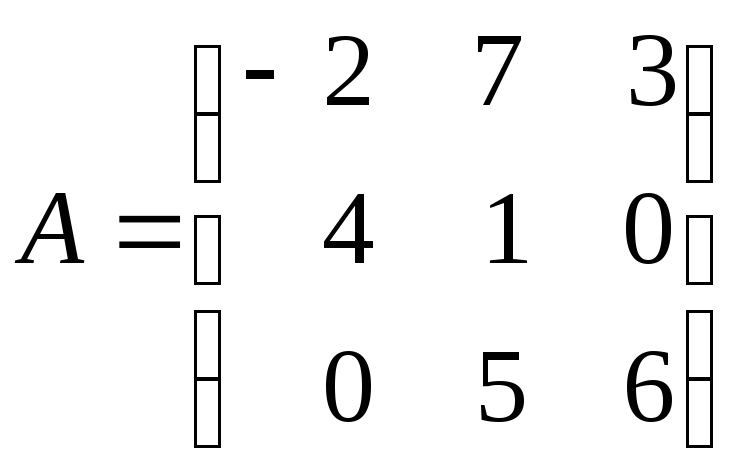 ,
,
![]() – единичная матрица
третьего порядка.
– единичная матрица
третьего порядка.
1.3. Найдите
произведения
![]() и
и
![]() матриц
матриц
![]() и
и
![]() .
.
1.4. Найдите
произведения
![]() и
и
![]() матриц
матриц
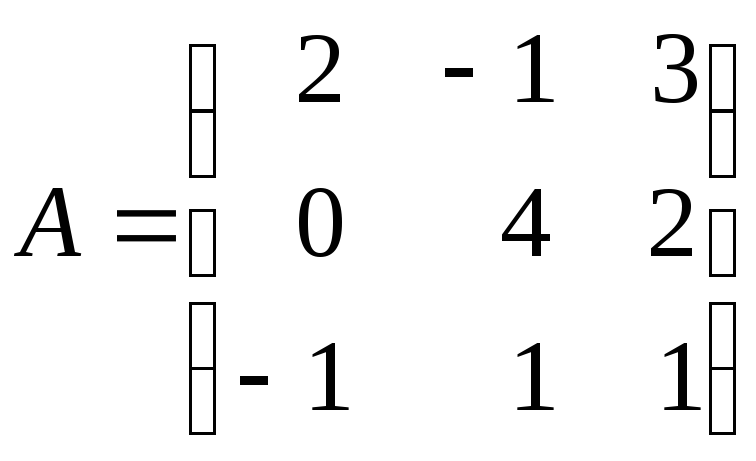 и
и
![]() .
.
1.5. Найдите
произведения
![]() и
и
![]() матрицы
матрицы
![]() .
.
1.6. Приведите к ступенчатому виду матрицу:
а)
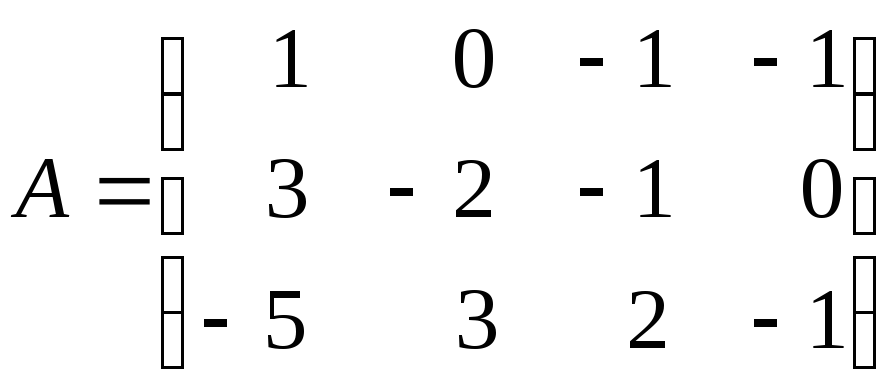 ; б)
; б)
 .
.
____________________________
1.7. Вычислите
матрицу
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() – единичная матрица
второго порядка.
– единичная матрица
второго порядка.
1.8. Найдите
произведение
![]() матриц
матриц
![]() ,
,
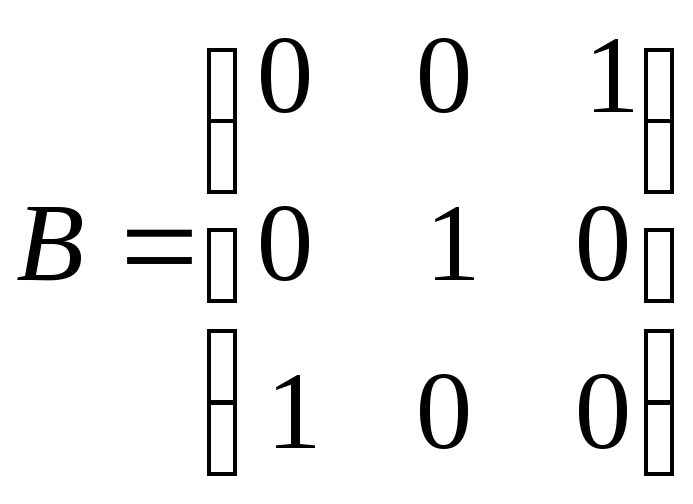 и
и
![]() .
.
1.9. Проверьте
коммутативность умножения матриц
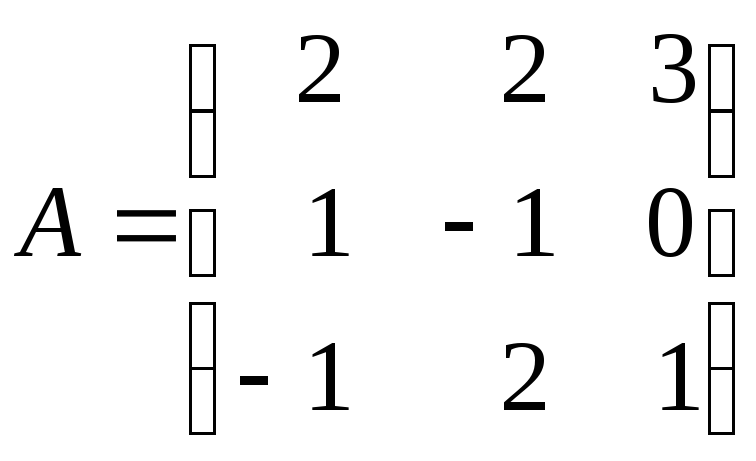 и
и
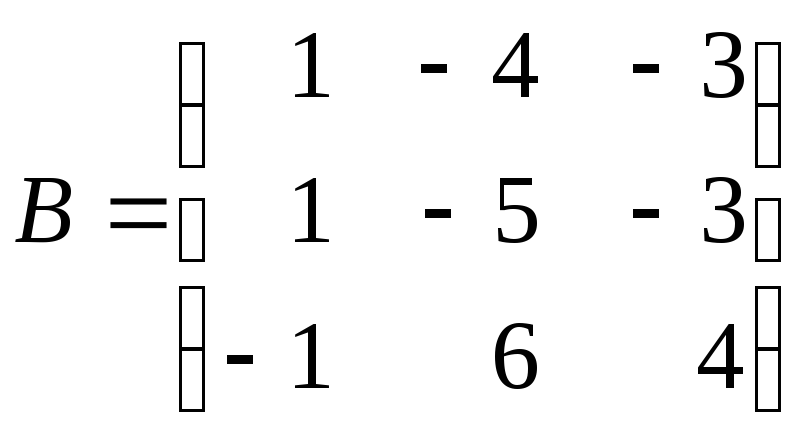 .
.
1.10. Приведите
к ступенчатому виду матрицу
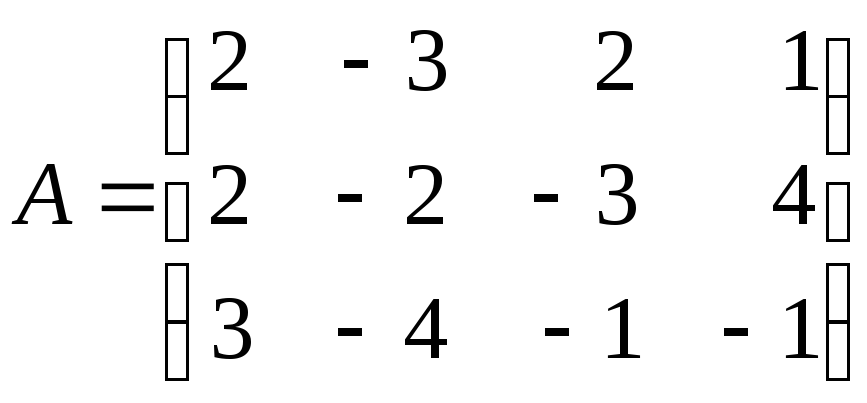 .
.
2. Определители
2.1. Вычислите определитель второго порядка:
а)
![]() ; б)
; б)
![]() ; в)
; в)
![]() .
.
2.2. Вычислите определитель третьего порядка с помощью «правила треугольников»:
а)
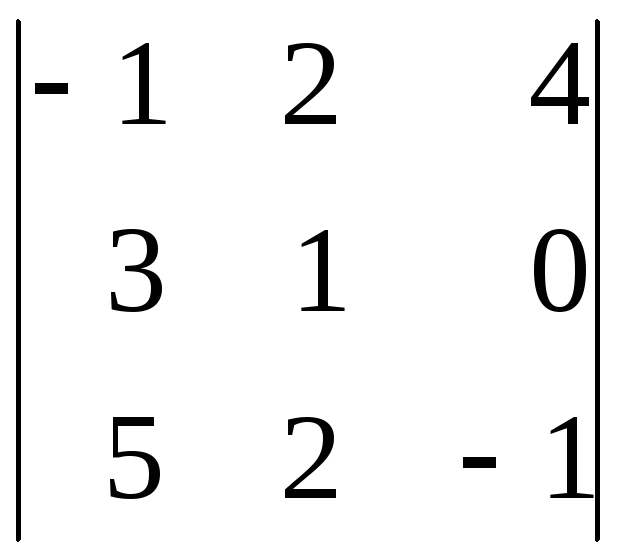 ; б)
; б)
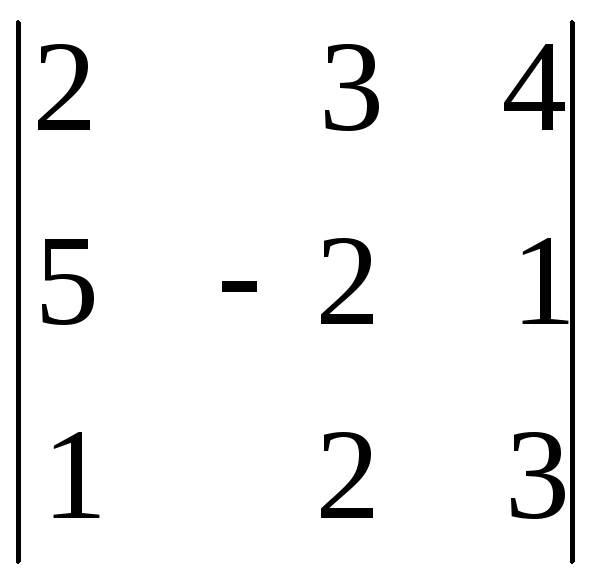 ; в)
; в)
 .
.
2.3. Вычислите определитель третьего порядка разложением по какой-нибудь строке или столбцу:
а)
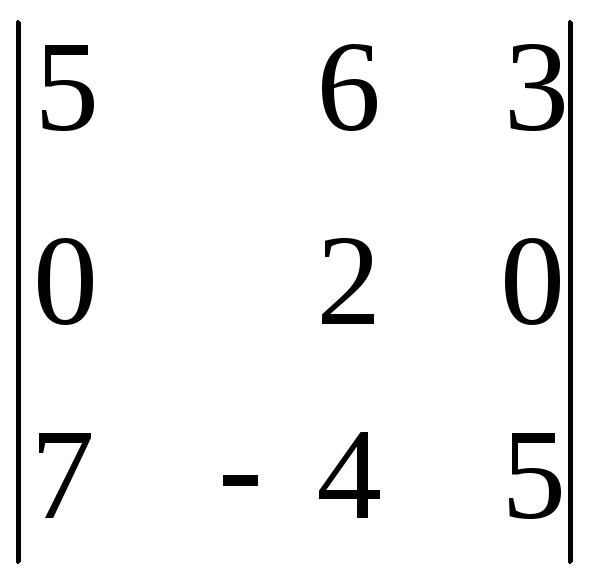 ; б)
; б)
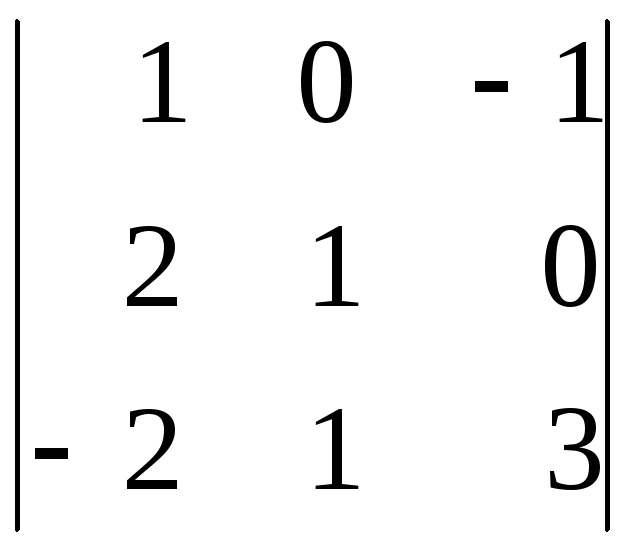 ; в)
; в)
 .
.
2.4. Вычислите определитель:
а)
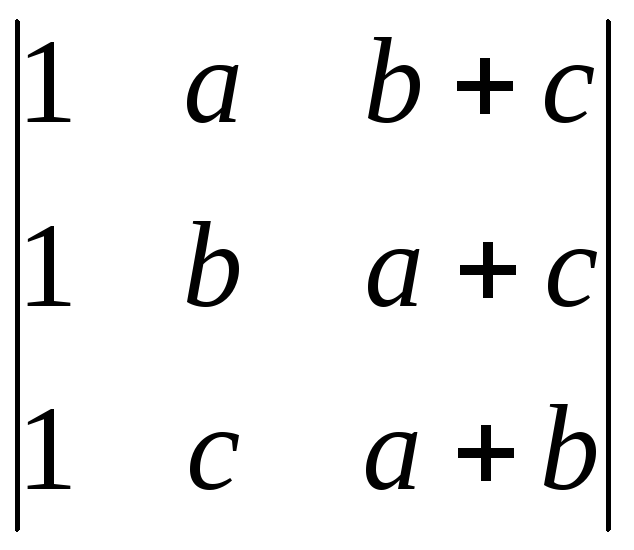 ; б)
; б)
 ; в)
; в)
 .
.
2.5. Решите уравнение:
а)
![]() ; б)
; б)
![]() ; в)
; в)
 .
.
____________________________
2.6. Вычислите определитель третьего порядка с помощью «правила треугольников»:
а)
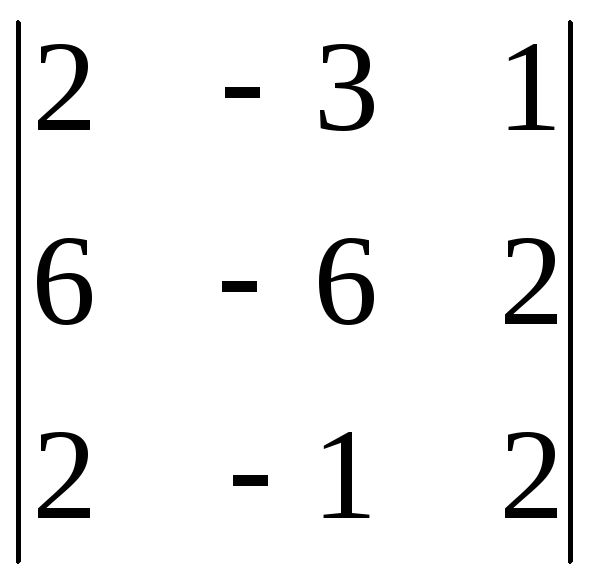 ; б)
; б)
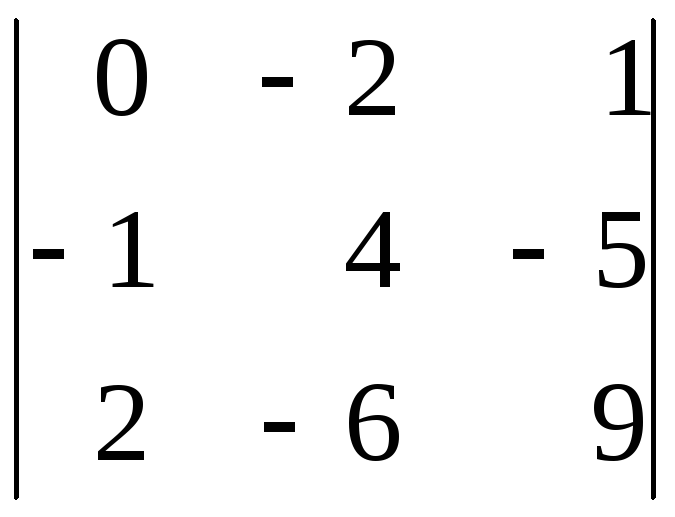 ; в)
; в)
 .
.
2.7. Вычислите определитель третьего порядка разложением по какой-нибудь строке или столбцу:
а)
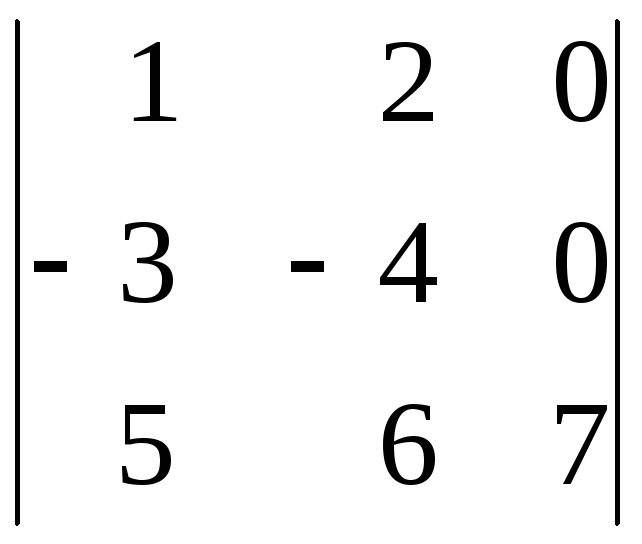 ; б)
; б)
 ; в)
; в)
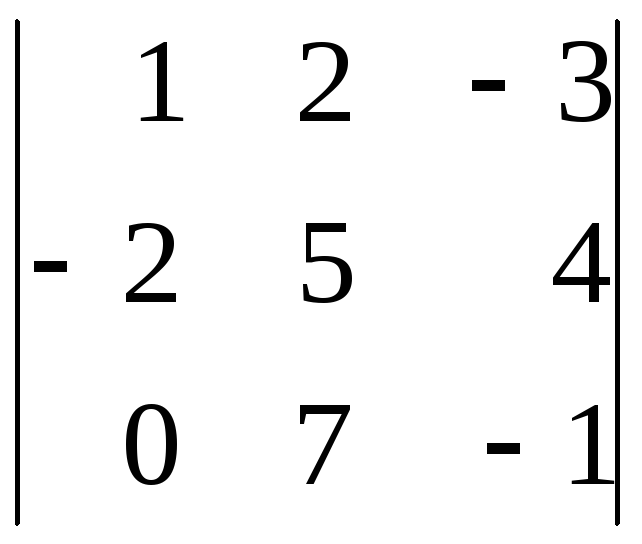 .
.
2.8. Вычислите определитель:
а)
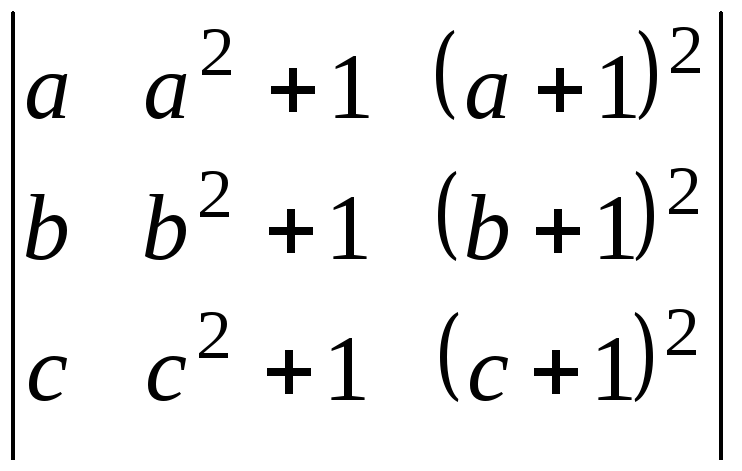 ;
б)
;
б)
 ; в)
; в)
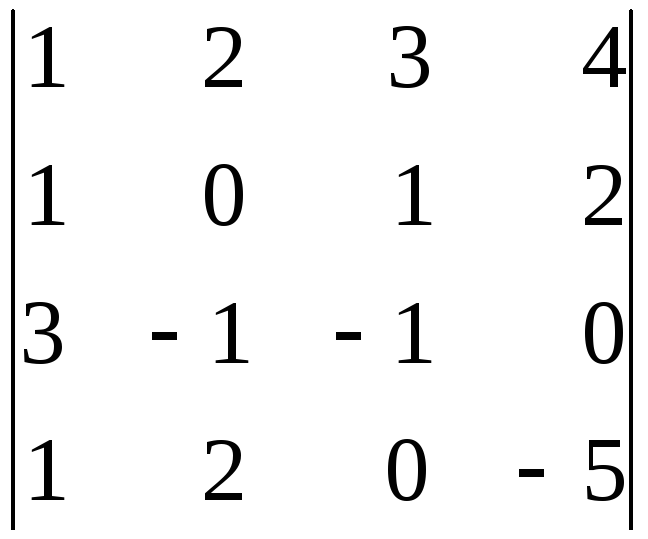 .
.
2.9. Решите уравнение:
а)
![]() ; б)
; б)
![]() ; в)
; в)
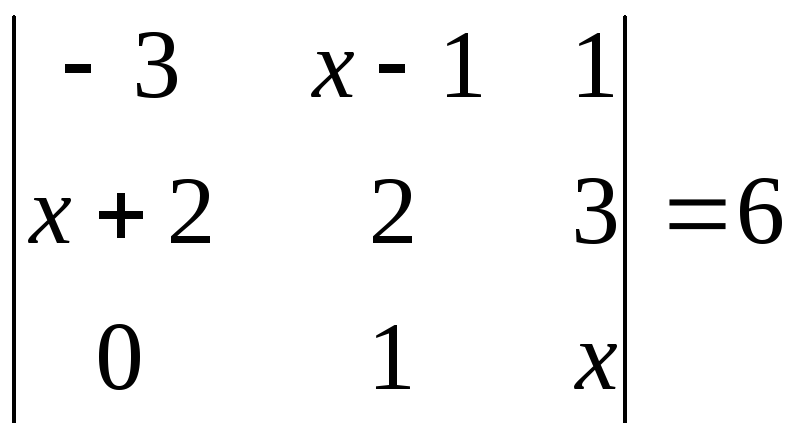 .
.
3. Обратная матрица
3.1. Определите, при каких значениях λ матрица А не имеет обратной:
а)
![]() ; б)
; б)
 ; в)
; в)
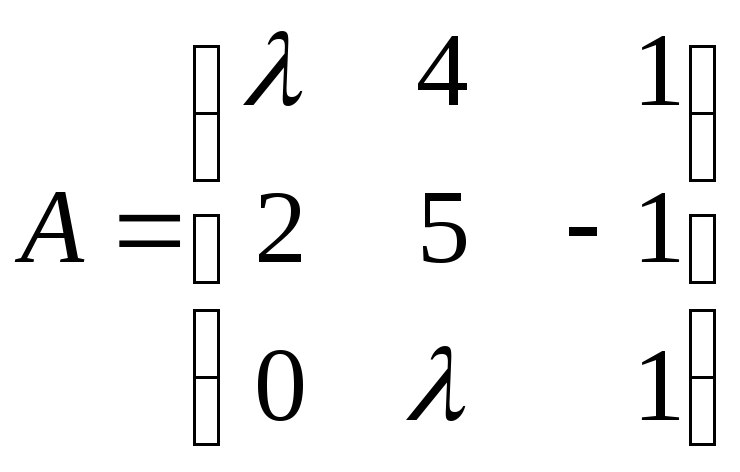 .
.
3.2. Используя алгебраические дополнения, найдите обратную матрицу для матрицы:
а)
![]() ; б)
; б)
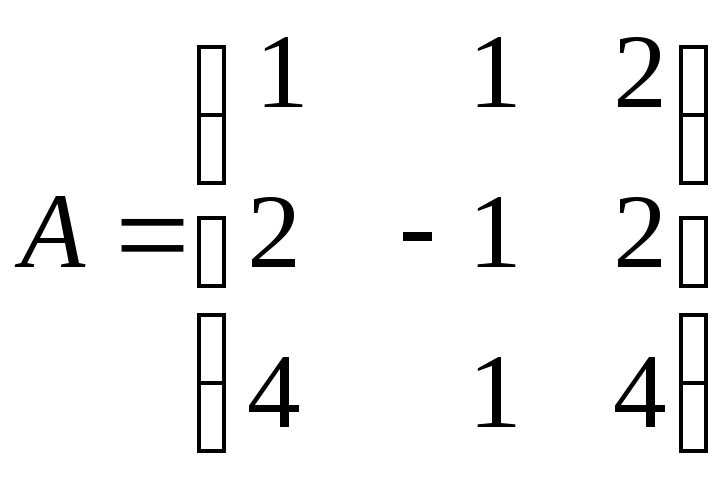 ; в)
; в)
 .
.
3.3. Используя элементарные преобразования, найдите обратную матрицу для матрицы:
а)
![]() ; б)
; б)
 ; в)
; в)
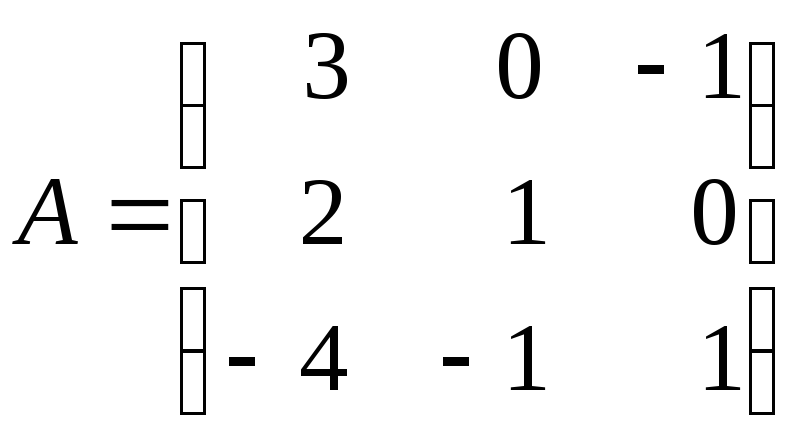 .
.
3.4. Решите матричное уравнение:
а)
![]() ; б)
; б)
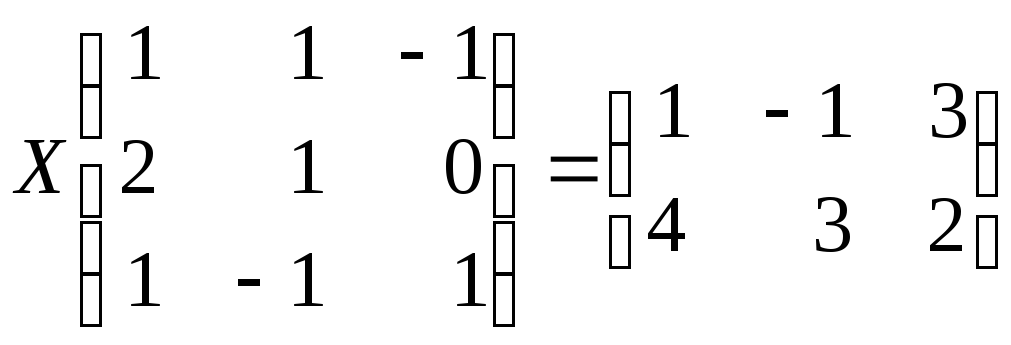 ;
;
в)
![]() .
.
____________________________
3.5. Найдите обратную матрицу для матрицы:
а)
![]() ; б)
; б)
 ; в)
; в)
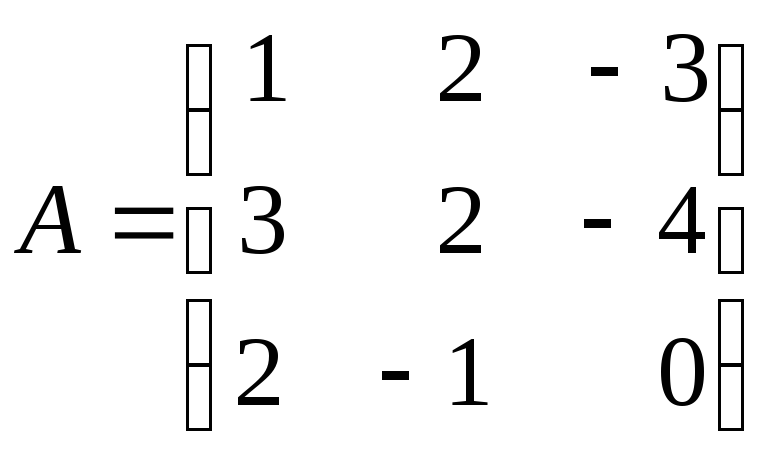 .
.
3.6. Решите матричное уравнение:
а)
 ; б)
; б)
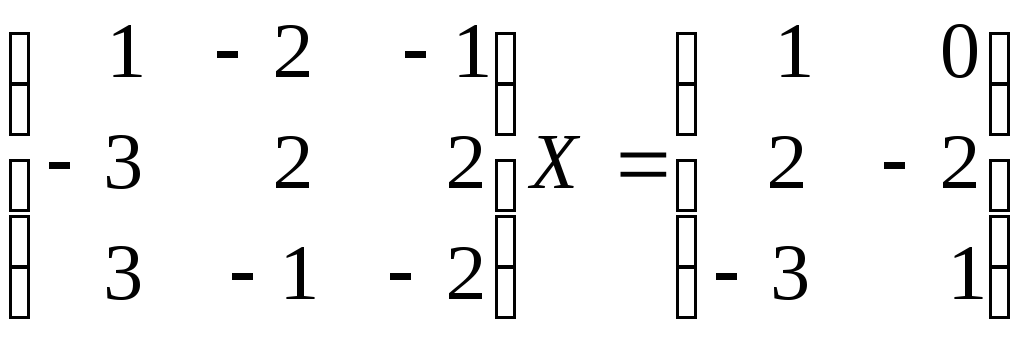 .
.
4. Ранг матрицы
4.1. Найдите ранг матрицы:
а)
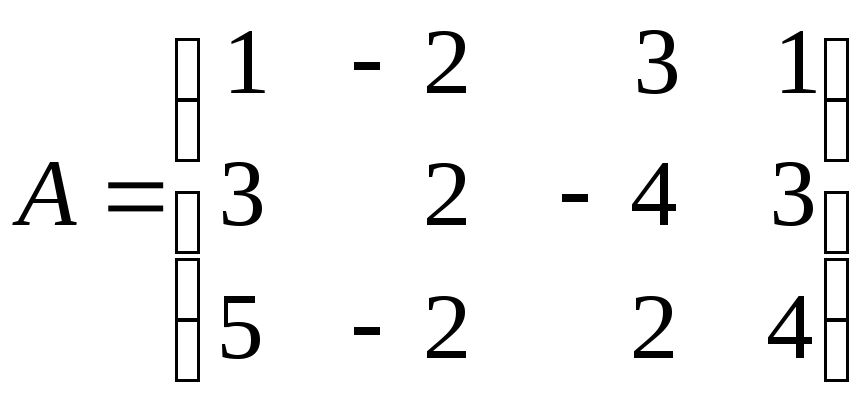 ; б)
; б)
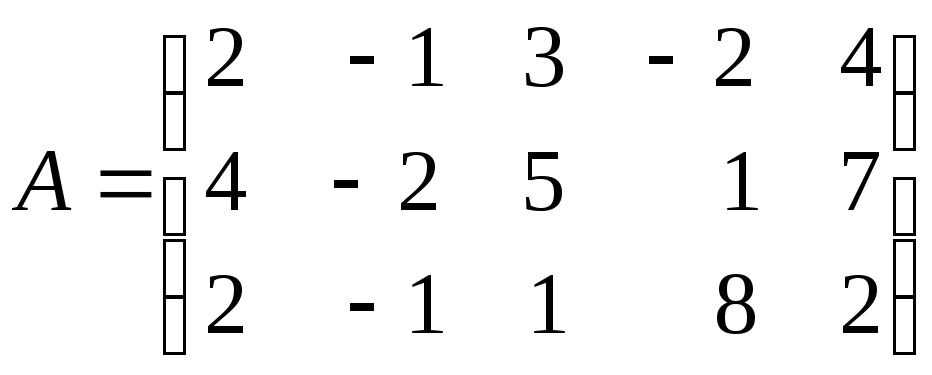 .
.
4.2. Определите, при каких значениях λ ранг матрицы А равен 3:
а)
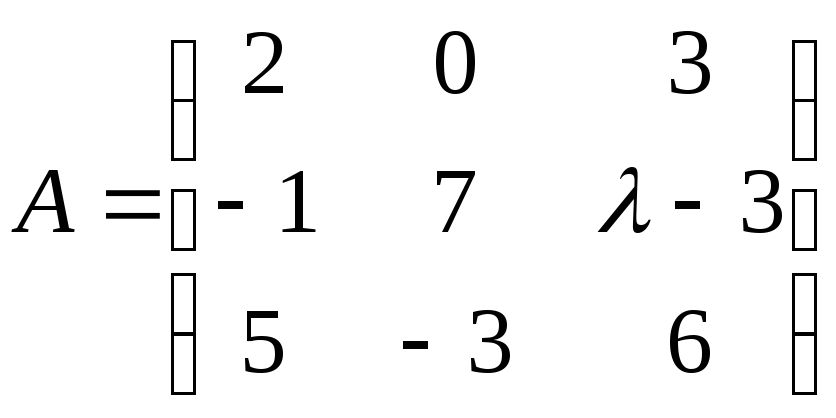 ; б)
; б)
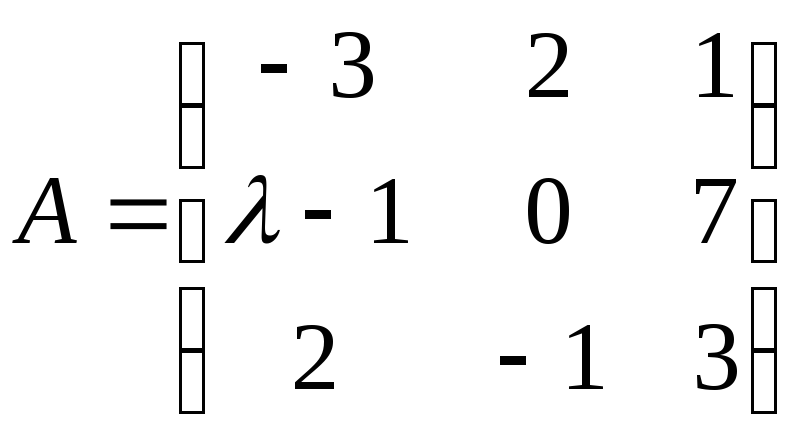 .
.
4.3. Найдите
ранг матрицы
![]() ,
где
,
где
![]() .
.
____________________________
4.4. Найдите ранг матрицы:
а)
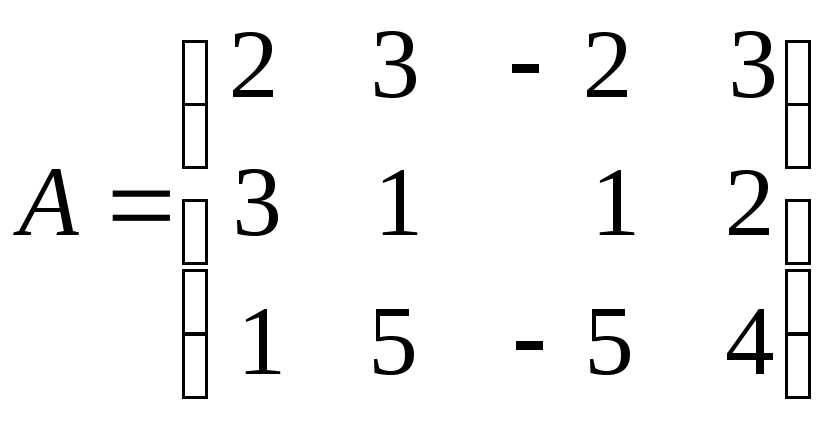 ; б)
; б)
 .
.
4.5. Определите,
при каких значениях λ
ранг матрицы
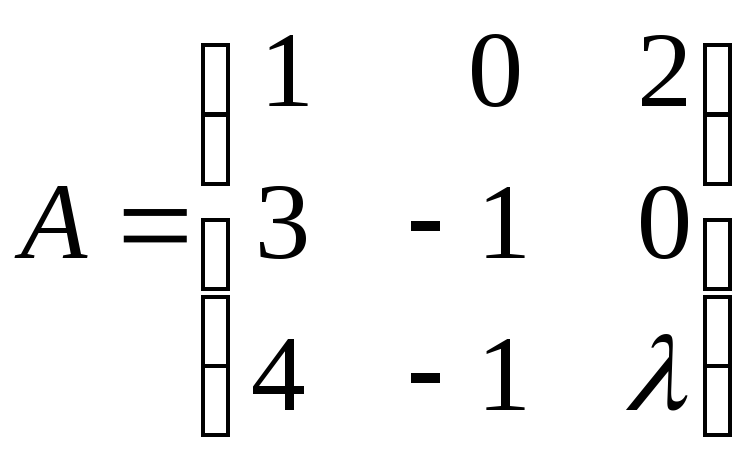 равен 3.
равен 3.
5. Дополнительные задачи
5.1. Найдите
произведения
![]() и
и
![]() матриц
матриц
![]() и
и
![]() .
.
5.2. Найдите
произведения
![]() и
и
![]() матрицы
матрицы
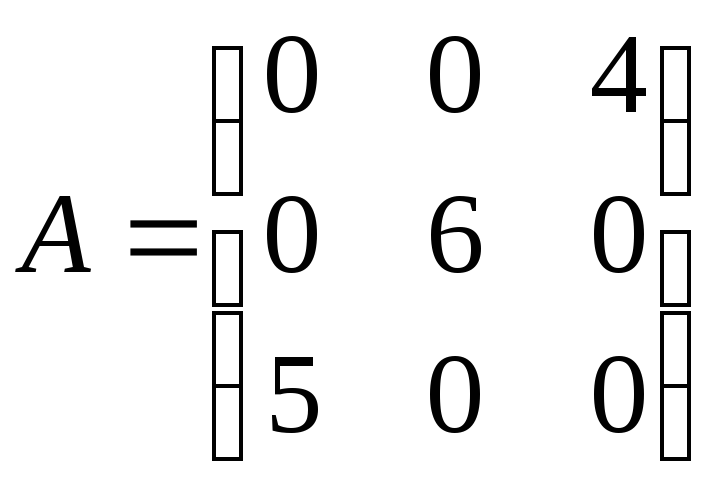 .
.
5.3. Вычислите
матрицу
![]() ,
где
,
где
 ,
,
![]() .
.
5.4. Приведите
к ступенчатому виду матрицу
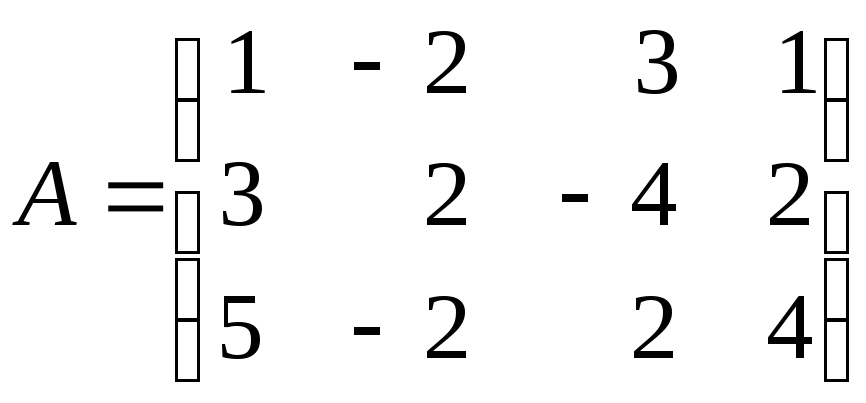 .
.
5.5. Вычислите определитель:
а)
![]() ; б)
; б)
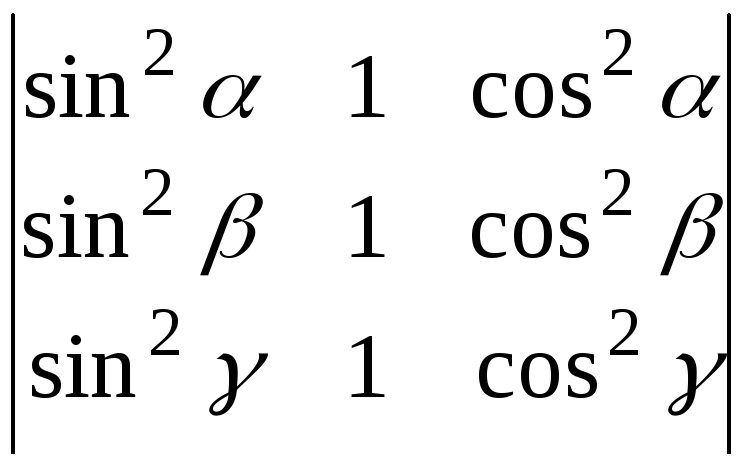 ; в)
; в)
 .
.
5.6. Решите уравнение:
а)
![]() ; б)
; б)
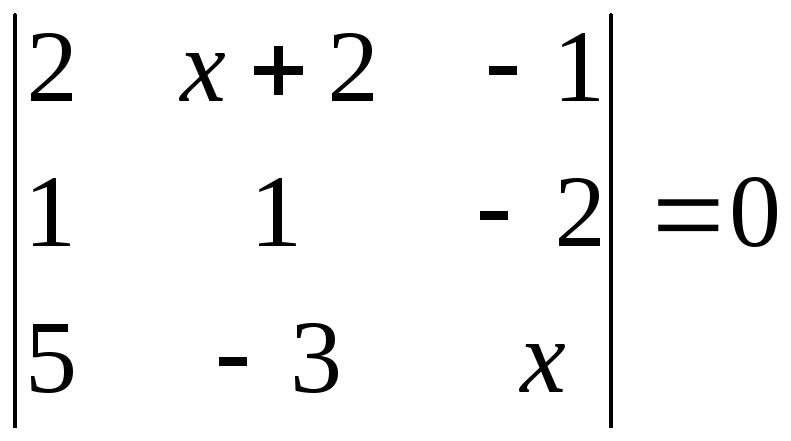 ; в)
; в)
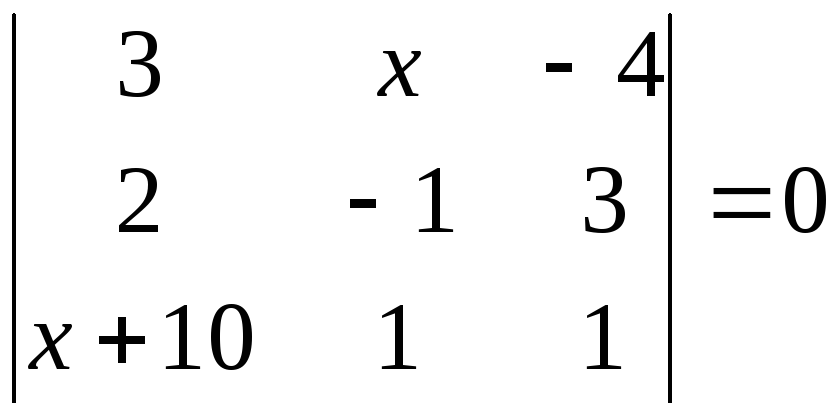 .
.
5.7. Найдите обратную матрицу для матрицы:
а)
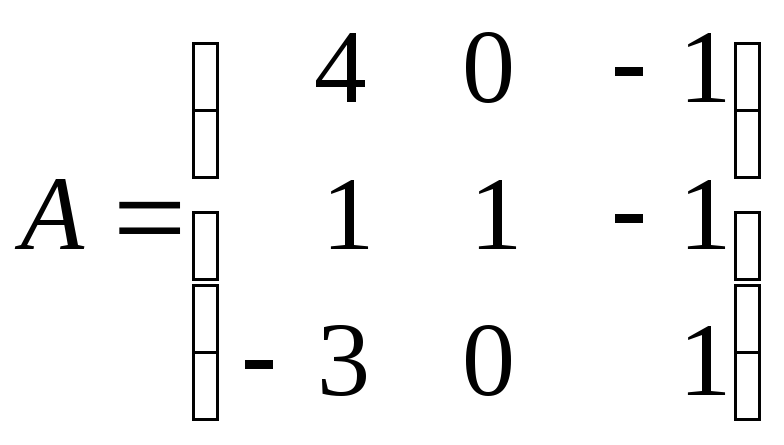 ; б)
; б)
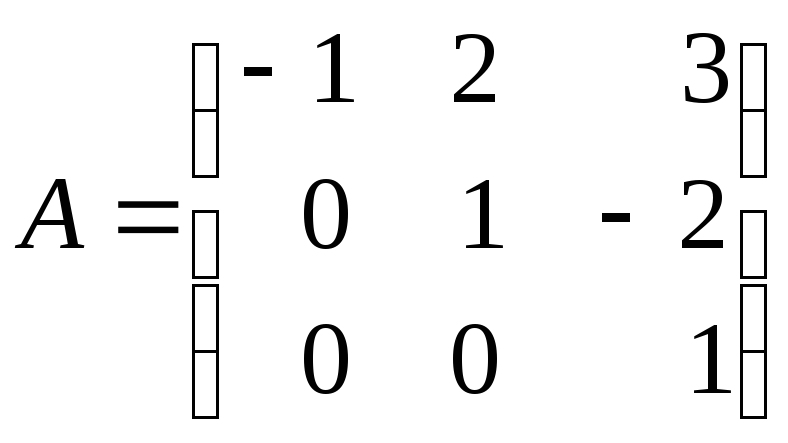 ; в)
; в)
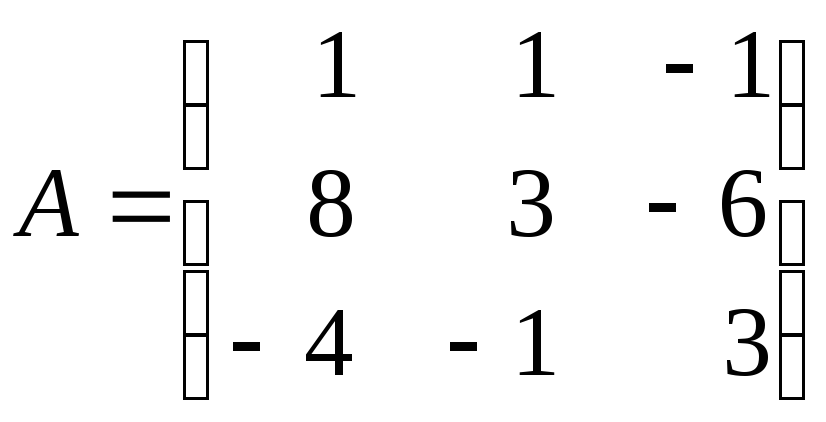 .
.
5.8. Решите матричное уравнение:
а)
![]() ; б)
; б)
![]() ;
;
в)
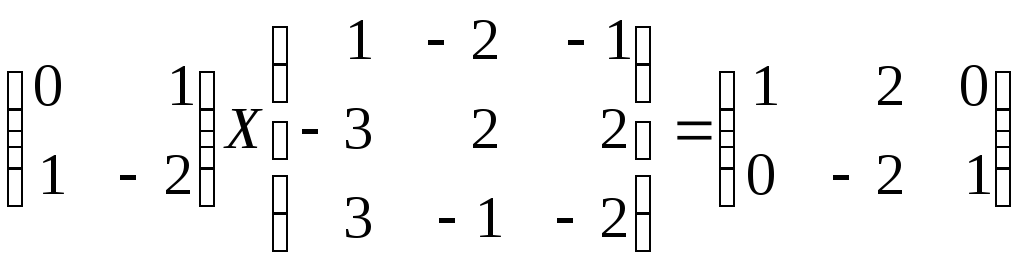 .
.
5.9. Найдите ранг матрицы:
а)
 ; б)
; б)
 .
.
Ответы
1. Операции над матрицами
1.1.
![]() .
1.2.
.
1.2.
 .
1.3.
.
1.3.
![]() ,
,
![]() .
.
1.4.
 ,
,
![]() .
1.5.
.
1.5.
![]() ,
,
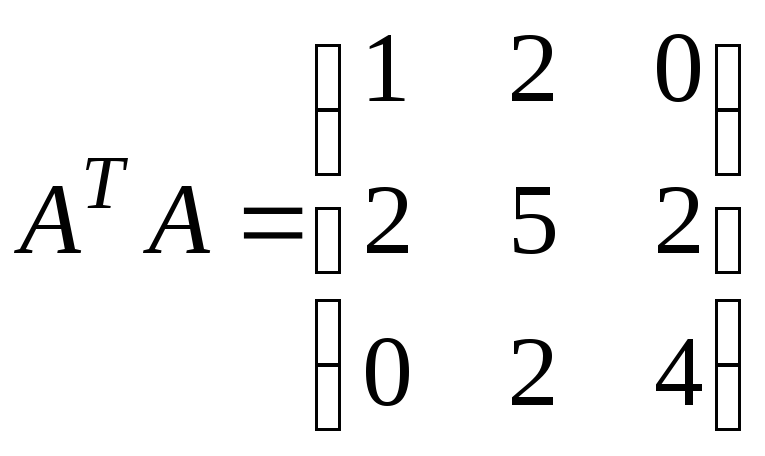 .
.
1.6.
а)
 ;
б)
;
б)
 .
1.7.
.
1.7.
![]() .
.
1.8.
![]() .
1.9.
.
1.9.
![]() .
1.10.
.
1.10.
 .
.
2. Определители
2.1.
а)
7; б)
![]() ;
в)
2b3.
2.2.
а)
11; б)
–10; в)
0.
2.3.
а)
8; б)
–1; в)
–12.
;
в)
2b3.
2.2.
а)
11; б)
–10; в)
0.
2.3.
а)
8; б)
–1; в)
–12.
2.4.
а)
0; б)
–6; в)
–48. 2.5.
а)
(2; –3); б)
![]() ;
в)
–4; 1; 2. 2.6.
а)
10;
;
в)
–4; 1; 2. 2.6.
а)
10;
б)
0; в)
7.
2.7.
а)
14; б)
39; в)
5. 2.8.
а)
0; б)
8; в)
–24. 2.9.
а)
(2; –1); б)
![]() ;
;
в) 1.
3. Обратная матрица
3.1.
а)
1; 2; б)
–1; 6; в)
–8; 1. 3.2.
а)
![]() ;
б)
;
б)
 ;
;
в)
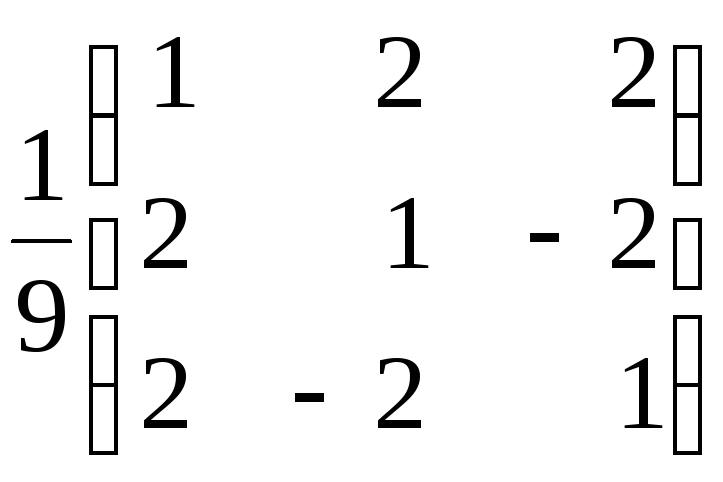 .
3.3.
а)
.
3.3.
а)
![]() ;
б)
;
б)
 ;
в)
;
в)
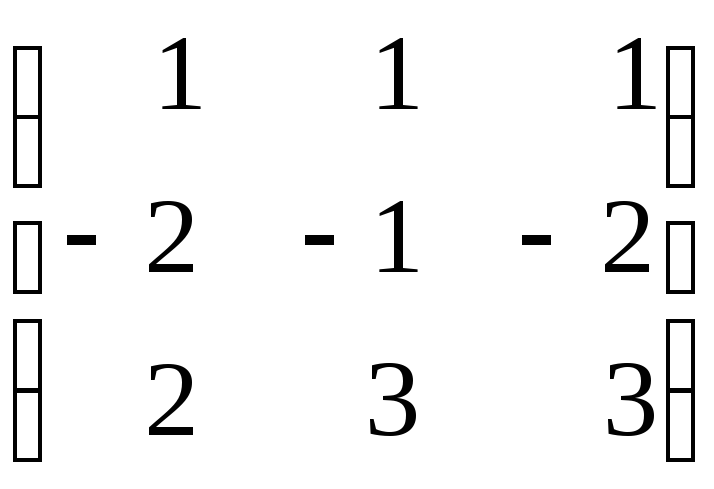 .
.
3.4.
а)
![]() ,
,
![]() ;
б)
;
б)
![]() ,
,
 ;
;
в)
![]() .
3.5.
а)
.
3.5.
а)
![]() ;
б)
;
б)
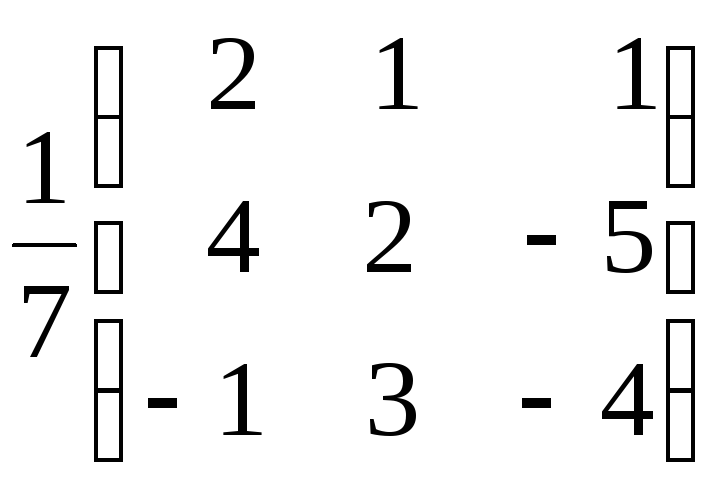 ;
в)
;
в)
 .
.
3.6.
а)
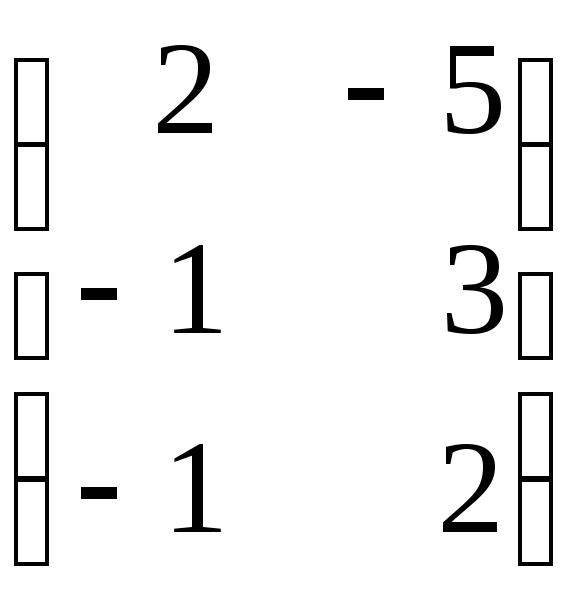 ,
,
![]() ;
б)
;
б)
 ,
,
 .
.
4. Ранг матрицы
4.1.
а)
3; б)
2. 4.2.
а)
![]() ;
б)
;
б)
![]() .
4.3.
2. 4.4.
а)
2; б)
3. 4.5.
.
4.3.
2. 4.4.
а)
2; б)
3. 4.5.
![]() .
.
5. Дополнительные задачи
5.1.
![]() ,
,
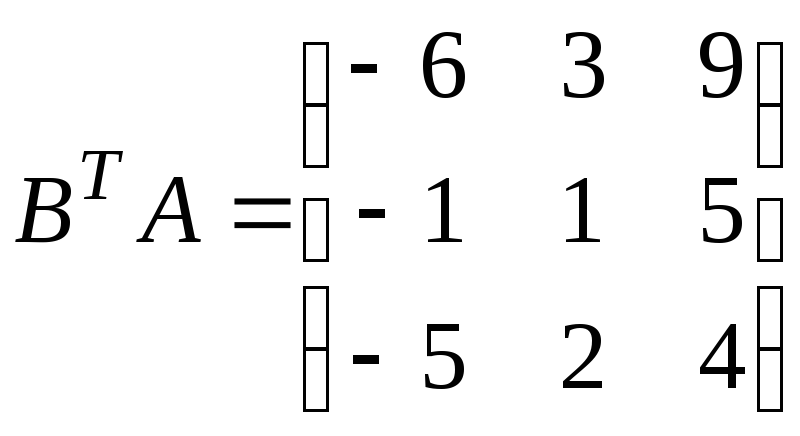 .
5.2.
.
5.2.
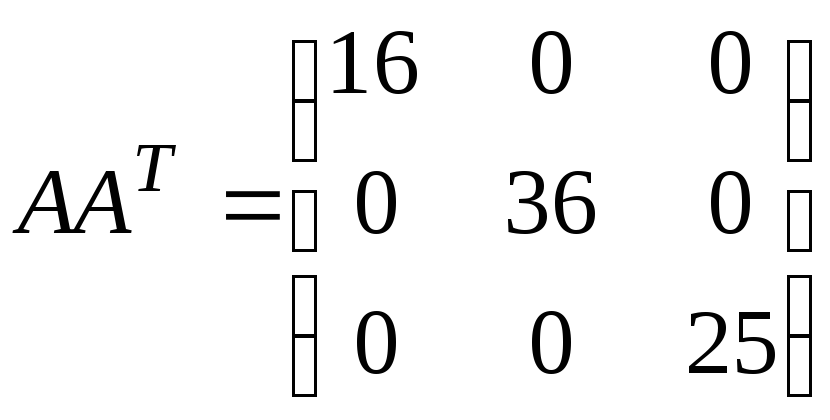 ,
,
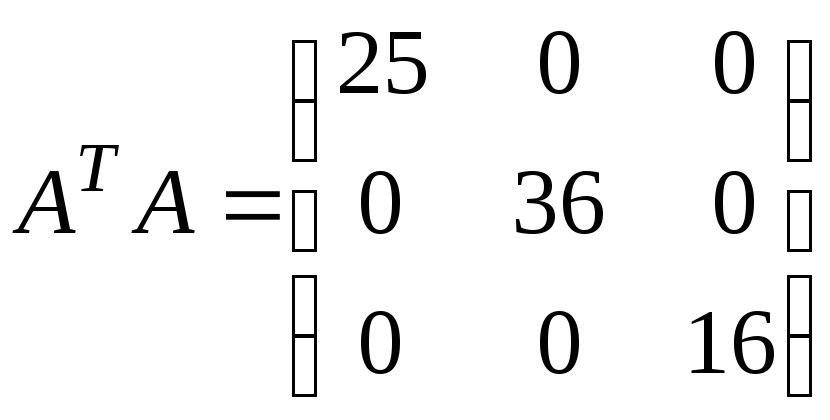 .
5.3.
.
5.3.
![]() .
5.4.
.
5.4.
 .
5.5. а)
1; б)
0;
.
5.5. а)
1; б)
0;
в)
–24. 5.6.
а)
1; 5; б)
–6; –4; в)
–10; 2. 5.7.
а)
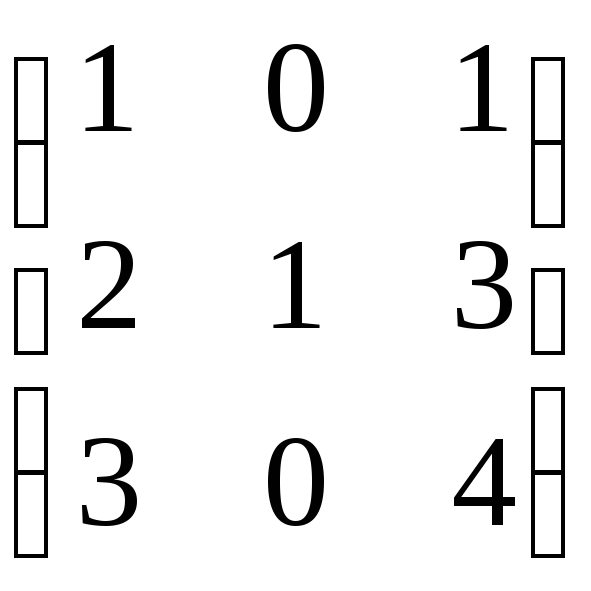 ;
б)
;
б)
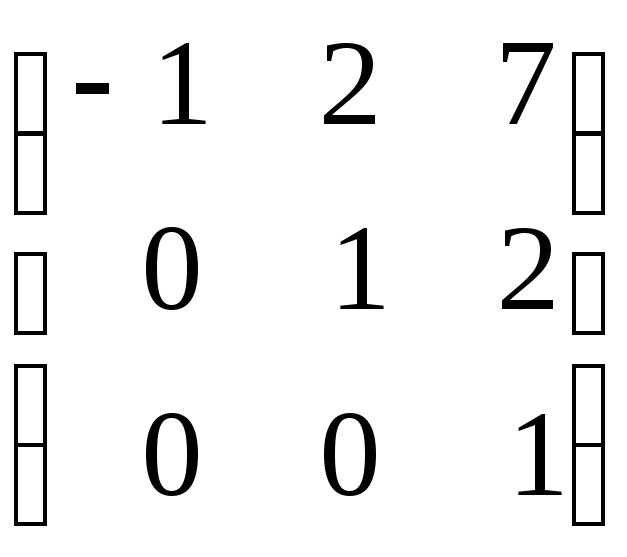 ;
;
в)
 .
5.8.
а)
.
5.8.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
5.9. а) 2; б) 2.
4.1. Методом окаймляющих миноров найдите ранг матрицы:
а)
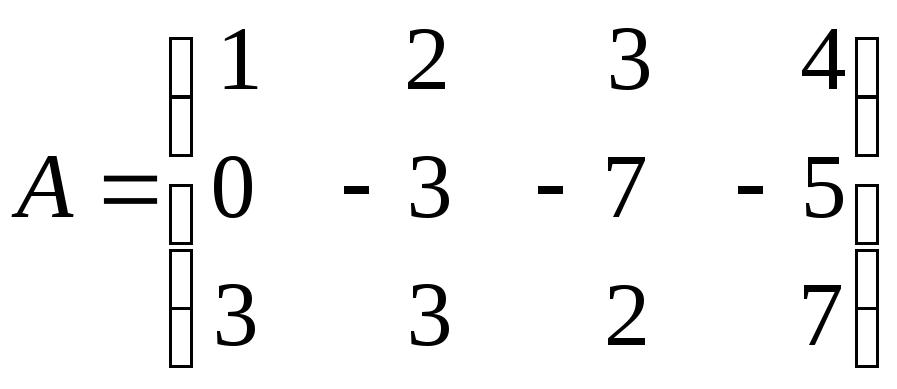 ; б)
; б)
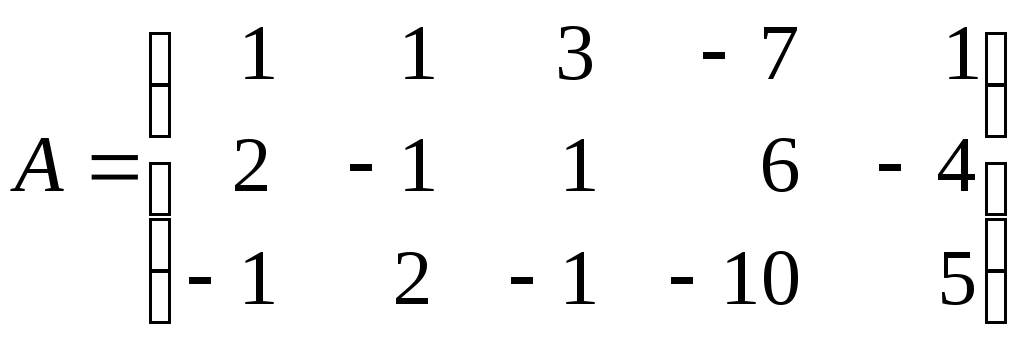 .
.
4.1. а) 2; б) 3.
4.4. Методом окаймляющих миноров найдите ранг матрицы:
а)
 ; б)
; б)
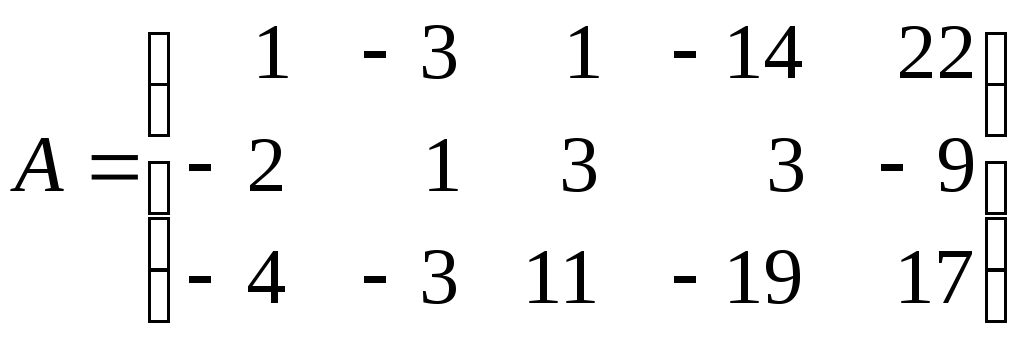 .
.
4.4. а) 2; б) 2.
4.3. Определите максимальное число линейно независимых строк (столбцов) матрицы:
а)
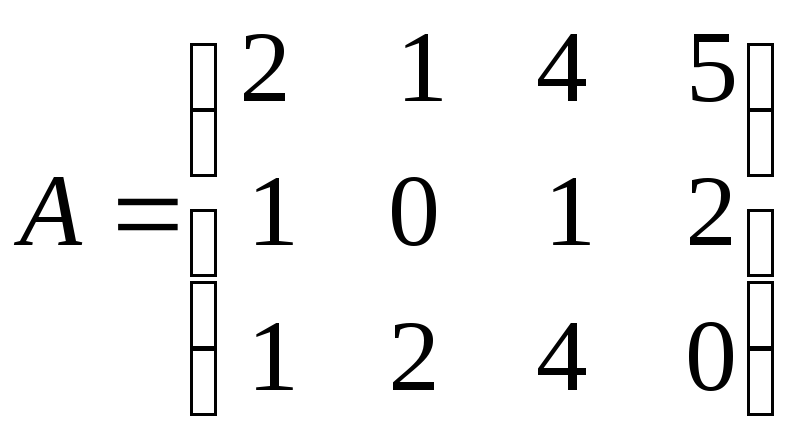 ; б)
; б)
 .
.
4.3. а) 3; б) 2.
5.9. Методом окаймляющих миноров найдите ранг матрицы:
а)
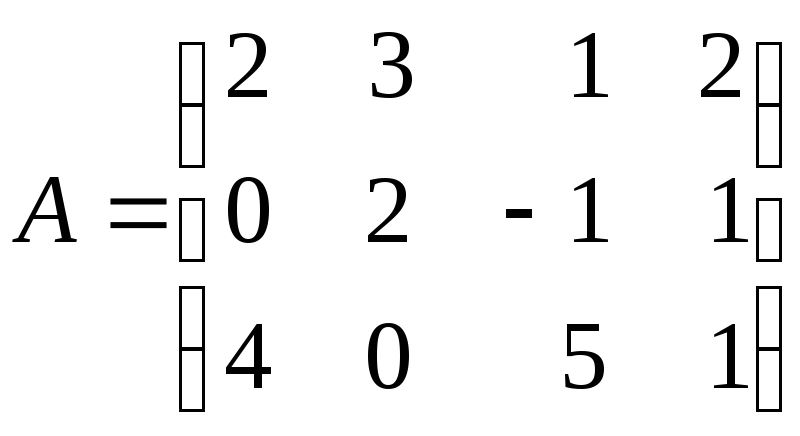 ; б)
; б)
 .
.
5.9. а) 2; б) 2.
