
- •1. Основные правила оформления чертежей
- •1.1. Форматы по ГОСТ 2.301-68*
- •1.2. Масштабы по ГОСТ 2.302-68*
- •1.3. Линии по ГОСТ 2.303-68*
- •1.4. Шрифт по ГОСТ 2.304-81*
- •1.5. Основная надпись по ГОСТ 2.104-68*
- •2. Основные правила выполнения изображений по ГОСТ 2.305-68*
- •2.1. Основные положения
- •2.2. Виды
- •2.3. Разрезы
- •2.4. Сечения
- •2.5. Выносные элементы
- •2.6. Некоторые условности и упрощения при выполнении изображений
- •2.7. Оформление изображений на чертежах
- •3. Графические обозначения материалов на чертежах по ГОСТ 2.306-68*
- •4. Нанесение размеров на чертежах по ГОСТ 2.307-68*
- •4.1. Общие положения
- •4.2. Общие правила нанесения размеров
- •4.3. Особенности нанесения линейных размеров. Нормальные линейные размеры
- •4.5. Нанесение размера радиуса дуги окружности. Нормальные радиусы скруглений
- •4.6. Нанесение длины дуги окружности
- •4.7. Нанесение размеров угла. Нормальные углы
- •4.8. Чертежи и размеры простейших геометрических фигур
- •4.9. Нанесение размеров формы и положения элементов детали
- •4.10. Нанесение размеров одинаковых и однотипных элементов
- •5. Основные особенности выполнения строительных чертежей
- •6. Аксонометрические проекции
- •6.1. Общие положения
- •6.2. Прямоугольная изометрическая проекция (изометрия)
- •6.4. Вычерчивание окружностей в аксонометрии
- •6.5. Примеры аксонометрических проекций различных предметов
- •Список рекомендуемой литературы
- •Оглавление

85
6. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ
6.1. Общие положения
Комплексные (технические) чертежи строят по методу прямоугольного проецирования на плоскости проекций, при этом количество изображений предмета на этих чертежах должно быть наименьшим, но полностью раскрывающим его форму и размеры. Такие чертежи обратимы, удобоизмеримы, но недостаточно наглядны, так как пространственный образ предмета в сознании очень часто приходится воспроизводить по нескольким его изображениям. Поэтому возникла необходимость в чертежах, которые были бы наглядны, но при этом обратимы и давали общее представление об относительных размерах и форме предмета.
Аксонометрической проекцией называют наглядное изображение предмета, полученное параллельным проецированием его на одну аксонометрическую плоскость проекций П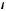 вместе с осями пространственной системы координат Oxyz, к которой он отнесен (предмет отнесен к системе координат, если известна его проекция на одну из координатных плоскостей.). Проекцию предме-
вместе с осями пространственной системы координат Oxyz, к которой он отнесен (предмет отнесен к системе координат, если известна его проекция на одну из координатных плоскостей.). Проекцию предме-
та на плоскость П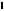 называют аксонометрической (аксонометрией);
называют аксонометрической (аксонометрией);
проекции координатных осей - соответствующими аксонометрическими осями (их упрощенно обозначают x, y, z вместо x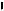 , y
, y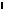 , z
, z ); отношение длины аксонометрической проекции отрезка, параллельного координатной оси, к натуральной длине отрезка - показателем искажения по соответствующей аксонометрической оси. Если направление проецирования перпендикулярно плоскости П
); отношение длины аксонометрической проекции отрезка, параллельного координатной оси, к натуральной длине отрезка - показателем искажения по соответствующей аксонометрической оси. Если направление проецирования перпендикулярно плоскости П  , то аксонометрию называют прямоугольной, а если нет, то косоугольной.
, то аксонометрию называют прямоугольной, а если нет, то косоугольной.
Для построения наглядных технических изображений ГОСТ 2.317-69* рекомендует стандартные аксонометрии, обладающие хорошей наглядностью.
6.2. Прямоугольная изометрическая проекция (изометрия)
Этот вид аксонометрии получается при одинаковом наклоне всех координатных плоскостей, связанных с предметом, к аксонометрической плоскости проекций. Поэтому в изометрии коэффициенты искажения по осям x, y и z одинаковы (они равны 0,82), а аксонометрические оси образуют между собой углы по 120О (рис. 6.1). Их можно построить с помощью циркуля или угольников с

|
86 |
|
|
|
углами 30О и 60О, расположив |
||
|
ось z вертикально. На рис. |
||
|
6.1 оси x и y проведены с |
||
|
уклоном 4:7 к горизонталь- |
||
|
ной линии чертежа. |
||
|
Для упрощения изомет- |
||
|
рию строят, используя приве- |
||
|
денные показатели искажения |
||
|
по осям, равные 1. В этом |
||
|
случае изображение предмета |
||
|
в изометрии |
выполняется в |
|
|
увеличенном масштабе 1,22:1. |
||
|
Прямоугольная изомет- |
||
|
рия наиболее удобна для |
||
Рис. 6.1 |
предметов |
криволинейной |
|
формы, длина, ширина и |
|||
|
|||
высота которых отличаются друг от друга не очень значительно. |
|||
6.3. Прямоугольная диметрическая проекция |
|||
|
(диметрия) |
|
|
Диметрия получается при одинаковом наклоне к аксонометрической плоскости координатных плоскостей xOy и yOz, поэтому показатели искажения по осям x и z одинаковы и равны 0,94, а по оси y - 0,47. Используя на практике приведенные показатели искажения (по 1 для осей x и z и 0,5 для оси y), диметрию выполняют в масштабе увели- 
чения 1,06:1.
При построении аксонометрических осей (рис. 6.2) ось
z проводят вертикально, а для
нанесения осей x и y |
исполь- |
|
зуют не углы их наклона к гори- |
||
зонтальной прямой |
чертежа |
|
(соответственно 7 10 и |
41 25 ), |
|
а их уклоны к этой |
прямой |
|
(соответственно 1:8 и 7:8). |
|
|
Прямоугольную диметрию |
||
целесообразно применять |
для |
|
предметов призматической и |
Рис. 6.2 |
|
87
пирамидальной форм, а также для предметов удлиненной формы, у которых длина значительно превышает ширину и высоту, направляя длину параллельно оси х или z. В этом случае длина не подвергается сильному искажению и не теряется представление о форме предмета и соотношении его основных размеров.
6.4. Вычерчивание окружностей в аксонометрии
Окружность, лежащая в координатной плоскости или плоскости, ей параллельной, проецируется в прямоугольной аксонометрии в эллипс, большая ось которого перпендикулярна “свободной” аксонометрической оси, а малая ей параллельна. Свободная аксонометрическая ось - проекция координатной оси, перпендикулярной плоскости окружности (например, для окружности, плоскость которой параллельна плоскости yOz, “свободной” осью является ось х).
Построение по приведенным показателям искажения эллипсов, в которые проецируются окружности, плоскости которых параллельны координатным, приведено для стандартных изометрии и диметрии на рис. 6.1 и 6.2 соответственно.
Большие оси этих эллипсов в изометрии равны 1,22d, а малые - 0,71d (d - диаметр окружности). Эллипсы в изометрии (рис. 6.1) строят по большим и малым осям (4 точки) и точкам на диаметрах, параллельных координатным осям (еще 4 точки).
В диметрии большие оси эллипсов равны 1,06d, а малые оси равны 0,35d для окружностей, лежащих в плоскостях xOy и yOz и им параллельным, и 0,94d для окружностей, расположенных в плоскости xOz и плоскостях ей параллельных. Для построения эллипсов в диметрии используют 8 точек, аналогичных точкам, по которым вычерчивают эллипс в изометрии (рис. 6.2). Чтобы точнее построить эллипсы, в которые проецируются окружности, параллельные плоскостям xOy и yOz, используют дополнительные точки, получаемые благодаря симметрии точек эллипсов относительно больших и малых осей.
На рис. 6.1 и 6.2 около осей эллипсов и их диаметров указаны приведенные показатели искажения по этим направлениям.
Аксонометрические проекции окружностей (дуг) большого радиуса, окружностей, не лежащих в плоскостях, параллельных координатным, и кривых линий строят по аксонометрическим проекциям их точек.

88
6.5. Примеры аксонометрических проекций различных предметов
Аксонометрию предмета обычно строят по его техническому чертежу, на котором могут быть указаны проекции осей пространственной системы координат Oxyz, к которой отнесен предмет.
Построение аксонометрии начинают с проведения аксонометрических осей.
Аксонометрические проекции фигур строят по аксонометрическим проекциям их характерных точек. Аксонометрические проекции точек строят по координатам этих точек с учетом показателей искажения по аксонометрическим осям.
Аксонометрические проекции отрезков строят по аксонометрическим проекциям двух их точек. Аксонометрические проекции параллельных прямых параллельны. При этом аксонометрические проекции прямых, параллельных координатным осям, параллельны соответствующим аксонометрическим осям и имеют такие же показатели искажения.
Для всех рассматриваемых далее предметов аксонометрия строилась по приведенным показателям искажения.
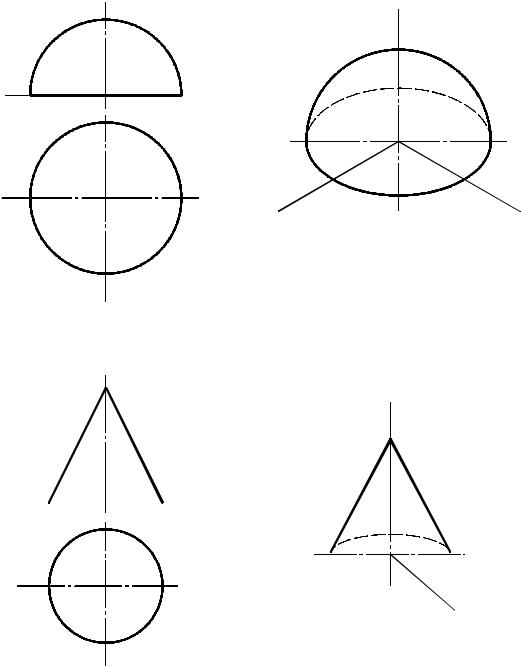
На рис. 6.3а, 6.4а и 6.5а представлены технические чертежи параллелепипеда, полусферы и конуса вращения соответственно, на рис. 6.3б и 6.4б приведены изометрии двух первых фигур, а на рис. 6.5б - диметрия третьей.
à) |
|
z2 |
|
á) |
|
|
|
|
z |
|
|
A2 |
B2 |
E2 |
D2 |
|
|
x2 |
a |
|
|
||
|
|
|
|
||
|
|
|
D |
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
B1 |
|
D1 |
|
|
E |
|
|
B |
|
||
x1 |
|
|
|
y |
|
|
|
x |
a |
||
|
|
|
|
||
|
|
|
b |
|
|
|
|
|
|
|
A
A1 E1
y1
Рис. 6.3
à) z2
x2
x1
y1
à) z2
x2 
x1
y1
89
á) z
x |
y |
Рис. 6.4
á)
z
x
y
Рис. 6.5
Очерком сферы при прямоугольном проецировании всегда является окружность радиусом, равным радиусу сферы R. При использовании приведенных показателей искажения радиус очерка сферы в изометрии увеличивают до 1,22R, а в диметрии - до 1.06R.
При построении аксонометрии предмета стремятся по возможности координатную плоскость xOy совместить с плоскостью основания предмета, а координатные оси - с его ребрами или осями симметрии.
90
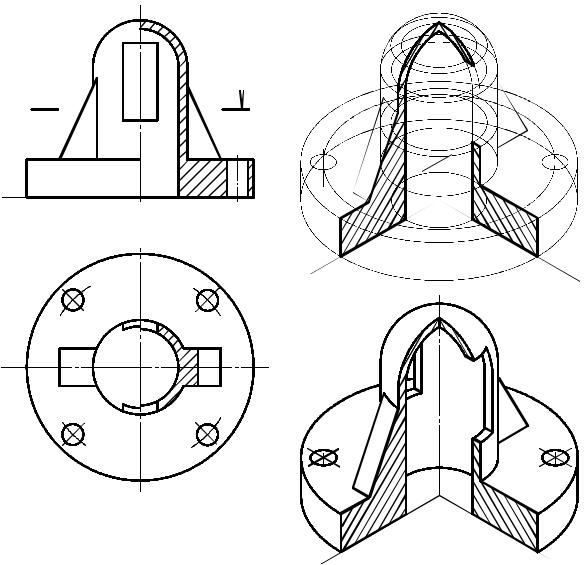
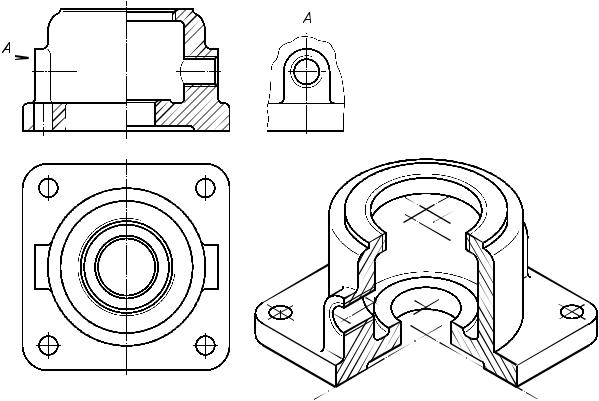
На рис. 6.6а и 6.7а приведены комплексные чертежи предметов, а на рис. 6.6в и 6.7б соответственно изометрические проекции этих предметов с вырезом одной четверти.
à) |
z2 |
á) |
z |
|
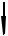 À
À
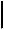 À
À
x2
À-À
x |
z |
y |
|
|
â)
x1
y1
Рис. 6.6 |
x |
y |
Вырез на изображениях, выполненных в аксонометрии, необходим так же, как и разрезы на технических чертежах, для выявления скрытых внутренних форм предмета.
Разрезы в аксонометрии можно построить двумя способами. Первый способ заключается в построении полного изображения
предмета в тонких линиях с последующим нанесением контуров сечений, образуемых каждой секущей плоскостью выреза, и удалением изображения отсеченной части предмета (рис. 6.6б).
По второму способу сначала строят контуры сечений предмета секущими плоскостями (на рис. 6.6б показаны основными линиями), а затем выполняют изображение остальной части предмета.
91
à)
z
á)
x |
y |
Рис. 6.7
Ваксонометрии, как правило, не применяют полные разрезы, при которых пропадает хотя бы одно из трех главных измерений предмета (длина, ширина, высота). В противном случае аксонометрия была бы лишена своего главного преимущества - наглядности.
Для определения направления штриховки в разрезах на аксонометрических осях откладывают произвольный отрезок b, а в диметрии на оси y - половину этого отрезка. Прямые, соединяющие концы отрезков, задают направление штриховки для соответствующих плоскостей (рис. 6.1 и 6.2).
Если секущая плоскость проходит через ребра жесткости, сплошные выступы или тонкие стенки, то сечения этих элементов деталей всегда заштриховывают. В аксонометрии не производят поворот в плоскость разреза отверстий, расположенных на круглых фланцах или дисках (рис. 6.6).
Ваксонометрии допускается не показывать мелкие конструктивные элементы предмета (фаски, скругления и т.п.). Линии плавного перехода одной поверхности в другую показывают условно тонкими линиями (рис. 6.7б).

92
à)
á)
Рис. 6.8
