
fel10E060
.pdf
61
Опишем вокруг окружности квадрат ABCE, также лежащий в плоскости  . Диагонали квадрата проходят через центр окружности O(O1 ,O2 ). Отметим восемь точек окружности (
. Диагонали квадрата проходят через центр окружности O(O1 ,O2 ). Отметим восемь точек окружности ( 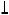 ,
,  ,
,  , ...), которые минимально необходимы для построения её перспективы.
, ...), которые минимально необходимы для построения её перспективы.
B2 |
C2 |
C2 |
ти |
Плоскость окружнос- |
||
2 |
|
|
и картинная плоскость |
|||
|
S2 |
Ï |
пересекаются по верти- |
|||
|
|
|||||
2 |
2 |
2 |
кальной прямой (4,C |
), где |
||
|
|
|
||||
O2 |
2 |
O2 |
41 |
C1= 1 |
Ï1 ; 4 2 |
x1 2 |
2 |
|
|
(точка 4 |
принадлежит |
||
m2  2
2
A2
x1 2
2
A1 B1
B1
 1
1 m1
m1
F
точки схода
..., (B,C).
|
2 |
|
2 |
2 |
E2 |
|
E2 |
|
42 |
O1 |
E1 C1 |
 41
41 C1 P
C1 P  31
31
предметной плоскости Ï1 );
(42,C )
)  x1
x1 2; точка C
2; точка C удалена от Ï1 на расстояние
удалена от Ï1 на расстояние
 42,C2
42,C2 , равное высоте верхней точки окружности
, равное высоте верхней точки окружности 
(рис. 15.14).
В плоскости Ï1 проведем проекции проецирующих прямых (S 1 ,A1 ),
21 |
(S 1,O 1) и (S1 ,E1 ). |
Отметим |
||
11 |
точки 11, 21, |
и 31 |
пересе- |
|
|
чения этих прямых с осно- |
|||
|
ванием картины k (k1). |
|
||
|
Через |
точку |
стояния |
|
f |
S1 проведем прямую f1 |
S1 |
||
1 |
и найдем точку F=f 1 |
k1 |
||
|
||||
Рис. 15.14 |
S1 (рис. 15.14) |
- основание |
||
F параллельных горизонтальных прямых |
(A,E), ( , |
), |
||
Перенесем на основание картины k в перспективе (рис. 15.15) точки 11 , 21 , 31 , 41 в виде точек 1, 2, 3, 4, используя расстояния от основания главной точки P:  P,1
P,1 =
= P,11
P,11 и т. д. Из точки 4 в перспективе проведем перпендикулярно k отрезок [4,C
и т. д. Из точки 4 в перспективе проведем перпендикулярно k отрезок [4,C ] длиной
] длиной  42,C2
42,C2 . Нанесем на этот отрезок точки E ,
. Нанесем на этот отрезок точки E , , O ,
, O , , соответствующие высотам точек A и E,
, соответствующие высотам точек A и E, и
и ,O,
,O, и
и  . Соединив точку схода F(
. Соединив точку схода F( F,P=F,P
F,P=F,P ) с точками E
) с точками E ,
, ,O
,O ,
, , C, получим перспективы параллельных горизонтальныхпрямых (A,E), (
, C, получим перспективы параллельных горизонтальныхпрямых (A,E), (  ,
, ), ..., (B,C). Прямые на рис. 15.15, проходящие через точки 1, 2, 3
), ..., (B,C). Прямые на рис. 15.15, проходящие через точки 1, 2, 3

62 |
|
|
|
m |
C |
C |
|
B |
|
||
|
|
|
|
F |
|
|
h |
P |
|
|
|
O |
|
O |
|
A |
|
|
|
A1 B1 |
E |
E C |
E |
O |
|||
1 |
|
1 |
1 |
m1 |
|
|
k |
1 2 P |
3 |
4 |
|
Рис. 15.15 |
|
|
|
перпендикулярно оси k, - перспективы вертикальных прямых (A,B), ( ,
, ), (C,E) с рис. 15.14. Точки пересечения этих перспектив с прямы-
), (C,E) с рис. 15.14. Точки пересечения этих перспектив с прямы-
ми ( F,E ), (F,O ), (F,C ) - перспективы точек |
A, |
, B; , O, |
; E, |
, |
C |
соответственно. Перспективы точек , , |
, |
получены как точки |
|||
пересечения перспектив диагоналей (A,C), (B,E) с прямыми (F, |
), (F, |
|
). |
||
Эллипс m на рис. 15.15, проходящий через точки , , |
..., |
, |
- |
||
перспектива заданной окружности.
Вторичной проекцией окружности m и вспомогательного квадрата является перспектива отрезка m1 предметной плоскости Ï1 (рис. 15.14). Поскольку точка 4 Ï1 , то вторичная перспектива окружности
Ï1 , то вторичная перспектива окружности
- отрезок |
m1 на рис. 15.15, лежащий на прямой (F,4) между точками |
A1 =(F,4) |
(1,B) и E1=(F,4) (3,C). |
Л Е К Ц И Я 16
ПЕРСПЕКТИВА (продолжение) 16.1. Перспектива плоского многоугольника
Если фигура образована преимущественно группами параллельных прямых, направления которых доминируют, то её перспективу обычно строят способом архитекторов, основанном на использовании точек схода перспектив этих групп параллельных прямых. Так как создание перспективы предмета рекомендуется начинать с его вторичной проекции, то с сущностью способа архитекторов познакомимся на примере построения перспективы многоугольника a[A,N,B,C,E,G,K,A], лежащего в предметной плоскости.

63
1 d N
F
 7 8
7 8
f 2
2
à) b
S1 h
á)
k
1
A |
K |
В плане (рис. 16.1, а) |
aбыли заданы многоугольник a, положение картинной плос-
B |
C |
|
кости |
1 (k), точка стояния S1 , |
||
4 |
P |
|
основание P главной точки |
|||
|
(P k |
(S1 |
,P) |
k). В поле |
||
|
E |
G |
перспективы |
(рис. 16.1, б) |
||
|
были |
заданы |
основание |
|||
|
3 |
|||||
|
|
картины k, горизонт h, главная |
||||
|
|
|
||||
f |
|
5 F |
|
|
|
1 |
6 |
F |
|
P |
|
|
|
||
b |
|
|
K |
|
|
|
|
d |
A |
|
C |
|
B |
||
|
|
||
N |
|
|
|
|
|
|
|
7 8 2 |
|
4 P |
|
точка P  h и её основание
h и её основание
P k ([P,P]
k ([P,P] k).
k).
F
a
 G
G
E

3 |
5 |
6 |
Рис. 16.1 |
Многоугольник a может рассматриваться как план некоторого здания. Соединим отрезком вершины A и B и построим сначала перспективу многоугольника [A,B,C,E,G,K,A]. Его контур в плане ограничен двумя группами (пучками) параллельных прямых. Первую группу составляют прямые (A,B) 
 (C,E)
(C,E) 
 (G,K), вторую - прямые
(G,K), вторую - прямые
(A,K)
 (B,C)
(B,C)
 (E,G).
(E,G).
Определим точки |
F =f k и F =f k (рис. 16.1,а) - основания |
точек схода F и F перспектив групп параллельных прямых, где f и |
|
f - проходящие через S1 |
вспомогательные прямые f (A,B), f (A,K). |
Найдем далее в плане картинные следы прямых (A,K), (B,C), (E,G), (A,B), (C,E), (K,G) - точки 1,2,3,4,5,6 их пересечения с основанием k. Перенесем эти точки на основание k в перспективе, откладывая в соответствующие стороны от точки P на рис. 16.1,б расстояния  1,P
1,P ,
,  2,P
2,P и т. д., взятые в плане. На горизонте h отметим точки схода F
и т. д., взятые в плане. На горизонте h отметим точки схода F и F
и F перспектив прямых, откладывая в разные стороны от главной точки P отрезки
перспектив прямых, откладывая в разные стороны от главной точки P отрезки  P,F
P,F
 =
=  P,F
P,F
 и
и  P,F
P,F
 =
= P,F
P,F
 .
.
64
Прямая (F ,1) - перспектива прямой (A,K); прямая (F
,1) - перспектива прямой (A,K); прямая (F ,2) - прямой (B,C); прямая (F
,2) - прямой (B,C); прямая (F ,3) - прямой (E,G); прямая (F
,3) - прямой (E,G); прямая (F ,4) - прямой (A,B); прямая (F
,4) - прямой (A,B); прямая (F ,5) - прямой (C,E); прямая (F
,5) - прямой (C,E); прямая (F  ,6) - прямой (G,K). Перспективы вершин многоугольника есть точки пересечения перспектив прямых, проходящих через эти вершины: A
,6) - прямой (G,K). Перспективы вершин многоугольника есть точки пересечения перспектив прямых, проходящих через эти вершины: A =(F
=(F ,4)
,4)
 (F
(F ,1); B
,1); B =(F
=(F ,4)
,4)
 (F
(F ,2) и т. д.
,2) и т. д.
[A ,B
,B ,C
,C ,E
,E ,G
,G ,K
,K ,A
,A ] - перспектива многоугольника [A,B,C,E,G,K,A].
] - перспектива многоугольника [A,B,C,E,G,K,A].
Через вершину N не проходят прямые доминирующих направлений. Её перспектива N может быть найдена с помощью перспектив d и b проходящих через N прямых предметной плоскости d k и b
k и b S1 , пересекающих основание k в точках 7 и 8 соответственно (рис. 16.1,а). На рис. 16.1,б перспектива d
S1 , пересекающих основание k в точках 7 и 8 соответственно (рис. 16.1,а). На рис. 16.1,б перспектива d  P,7, а перспектива b
P,7, а перспектива b 
 k
k b
b  8 (см. свойства перспектив прямых предметной плоскости). Перспектива N =d
8 (см. свойства перспектив прямых предметной плоскости). Перспектива N =d  b . [A ,N ,B ,C ,E ,G ,K ,A ] - искомая перспектива a
b . [A ,N ,B ,C ,E ,G ,K ,A ] - искомая перспектива a заданного многоугольника a, которая строится как совокупность перспектив его сторон и вершин.
заданного многоугольника a, которая строится как совокупность перспектив его сторон и вершин.
16.2. Выбор положения точки зрения и картины
Основная задача перспективы - показать, как будет выглядеть проецируемое сооружение после его возведения. Перспективу объекта обычно строят по ортогональным чертежам его плана и фасадов. Наглядность и информативность перспективного изображения определяются рациональным выбором параметров перспективы - положения наблюдателя и картинной плоскости, хотя формулы, гарантирующей их оптимальный выбор, нет.
Положение наблюдателя (направление взгляда, положение точки зрения по высоте и в плане) должно быть реальным и соответствовать существующей или запроектированной планировке. Оно зависит от изображаемого объекта и целевого назначения перспективы: получить изображение, наиболее полно и выразительно отражающее внешний облик и объёмно-пространственную структуру сооружения; оценить композиционную связь объекта с окружающей застройкой, ландшафтом местности, подъездными путями; показать объект таким, каким его будут видеть зрители из мест наиболее вероятного их появления; получить изображение интересующей части объекта и т. д.
Выбрав соответствующее цели перспективы направление взгляда, приступают к определению положения точки зрения.
Взависимости от высоты точки зрения различают перспективы
свысоким, низким и нормальным горизонтом. Перспективы с высо-

65
ким горизонтом (все или большинство точек объекта расположены ниже горизонта) применяют для изображения значительных пространств - плана местности, поселков, городских кварталов, транспортных развязок, мостовых переходов и т. д. Если при этом высота горизонта превышает 100 м, то перспективу называют “перс- пективой с птичьего полета”. Перспективы с низким горизонтом (все или большинство точек объекта расположены выше горизонта) используют для изображения сооружений, расположенных на возвышенности, берегу реки и т. д., при взгляде на них снизу. Наиболее распространены перспективы с нормальным горизонтом, расположенном на высоте роста человека 1,5...2,0 м. При построении перспективы автомобильной дороги высоту горизонта выбирают на уровне глаз сидящего водителя.
Чтобы получить достоверный по форме и пропорциям образ объекта, надо правильно выбрать расстояние от него до наблюдателя (дистанционное расстояние), позволяющее охватить объект одним взглядом. Это расстояние зависит от строения глаза человека и восприятия им окружающего мира. Исследованиями физиологов и психологов установлено, что четкая видимость объекта возможна при расположении его внутри конуса зрения с углом 28...37О при вершине, а умеренная видимость - с углом 18..53О. Вершина конуса зрения находится в оптическом центре хрусталика глаза, ось вращения конуса совпадает с главной проецирующей прямой (S,P), а угол при его вершине называется углом зрения.
Для перспектив с нормальным горизонтом обычных объектов положение точки зрения в плане устанавливают по горизонтальному углу зрения a между проекциями крайних лучей зрения (рис. 16.2). Допустимым углам a=18...53О соответствуют дистанционные расстояния 3L...L (L - наибольший габаритный размер объекта), рекомендуемым углом a=28...37О - дистанционные расстояния 2L...1,5L. С более близких точек зрения (a>53О) рассматривать объект трудно, на перспективных изображениях возникают чрезмерные искажения. При значительном удалении точки зрения (a<18О) усложняется построение перспективы.
Для перспектив с высоким горизонтом и перспектив высотных объектов (их высота больше длины и ширины) с нормальным горизонтом угол зрения уменьшают по сравнению с углом зрения для перспектив с нормальным горизонтом обычных объектов. Это достигается удалением центра перспективы на большее расстояние [4], [7], [8], [9], [10], [11].

66
Различают перспективу фронтальную - картина Ï параллельна одному из фасадов объекта и рассматриваемую здесь, более распространенную перспективу угловую - картина Ï не параллельна основным плоскостям фасадов, а соответствующим образом наклонена к ним.
не параллельна основным плоскостям фасадов, а соответствующим образом наклонена к ним.
Картинную плоскость Ï на комплексном чертеже задают горизонтальным следом (основной проекцией) Ï1 так, чтобы след Ï1 был перпендикулярен проекции главного луча в плане и составлял с одной из сторон плана, чаще всего с главным фасадом, угол b=20...35O
|
ÔАСАД |
(предельное значение 45О). |
|||||
|
При этом проекция главного |
||||||
|
|
||||||
|
|
луча должна |
находиться |
||||
|
h |
(рис. 16.2) в средней трети |
|||||
|
ширины |
B |
перспективного |
||||
x1 2 |
|
изображения или угла a в |
|||||
|
плане и может совпадать с |
||||||
|
|
||||||
|
ÏËАÍ |
биссектрисой этого угла. Ряд |
|||||
|
3 2 1 |
специалистов |
считает, что |
||||
|
последнее |
условие |
способ- |
||||
|
|
ствует |
получению |
более |
|||
|
|
достоверного по пропорциям |
|||||
b |
P |
образа объекта. |
|
||||
Картину можно провес- |
|||||||
|
|||||||
|
|
||||||
|
|
ти через какие-то элементы |
|||||
|
|
объекта, например, ближнее |
|||||
|
|
вертикальное |
ребро, |
чтобы |
|||
|
|
эти элементы |
проецирова- |
||||
|
|
лись в истинную величину в |
|||||
|
S1 |
масштабе |
ортогональных |
||||
|
проекций или |
в масштабе |
|||||
|
Рис. 16.2 |
||||||
|
|
|
|
|
|
||
перспективы.
Большое значение для восприятия объекта имеет масштабирование его перспективного изображения. Напомним, что при параллельном проецировании масштабом чертежа называют отношение длины проекции отрезка, параллельного плоскости проекций, к длине отрезка в натуре. Это определение не относится к центральному проецированию. Масштаб перспективы зависит от положения объекта относительно картинной плоскости и положения точки зрения относительно картинной и предметной плоскостей.

67
Если перспектива объекта строится по его ортогональным проекциям и все измерения фигур картинной плоскости выполняются с учетом масштаба этих проекций, то считается, что масштабом перспективы является масштаб ортогональных проекций.
Требуемую величину перспективного изображения можно получить параллельным перемещением картины вдоль главного луча. Такое перемещение влияет только на размеры изображения - они тем больше, чем больше расстояние от точки S до картины Ï . Часто главное расстояние  S,P
S,P выбирают в зависимости от необходимой ширины B перспективного изображения. Изображение объекта нужного размера можно получить без перемещения картины, увеличивая (уменьшая) в соответствующее число раз высоту горизонта и величины всех отрезков, переносимых с плана и фасадов на картину.
выбирают в зависимости от необходимой ширины B перспективного изображения. Изображение объекта нужного размера можно получить без перемещения картины, увеличивая (уменьшая) в соответствующее число раз высоту горизонта и величины всех отрезков, переносимых с плана и фасадов на картину.
Рассмотрим один из вариантов выбора положения точки зрения в плане на ортогональном чертеже схематизированного здания (рис. 16.3) при нормальном горизонте h и условии, что в перспективе должны быть видны главный и правый боковой фасады здания. Пусть угол зрения в плане a=30О, а картинная плоскость проходит через правое, ближнее к наблюдателю ребро здания, что не является обязательным, и образует с главным фасадом угол
b=40О.
Через главную точку плана здания проведём след картинной плоскости Ï1  k1 под выбранным углом b к проекции главного фасада.
k1 под выбранным углом b к проекции главного фасада.
Из крайних точек плана здания A и B построим перпендикуляры к основанию картины k1 , пересекающие его в точках 1 и 2. Отрезок [1,2] разделим на три равные части и в средней части выберем основание P - проекцию главной точки P картины. Перпендикуляр к основанию k1 , проходящий через точку P, - проекция главного луча, на которой расположена точка стояния S1 .
Считая проекцию главного луча биссектрисой угла зрения a в плане, из точек A и B плана здания под углом 15О к построенным перпендикулярам проводим прямые. Эти прямые образуют с проекцией главного луча углы 15О и пересекают её в точках 3 и 4. Середину отрезка [3,4] примем за точку стояния S - проекцию точки зрения S.

68
Фасад
h
x1 2
2
Ïëàí B
A |
2 |
|
P
b=40O
1
a=30 |
3 |
|
|
Рис. 16.3 |
S1 4 |
|
Проекция главного луча (S1 ,P) не совпадает с биссектрисой действительного угла зрения в плане между прямыми (S1 ,A) и (S1 ,B), величина действительного угла - с величиной заданного угла 30О. Однако эти несовпадения настолько не существенны, что практически не сказываются на перспективном изображении (рис. 16.4, а).
Если полученное положение точки стояния S1 не отвечает требованиям, предъявляемым к перспективному изображению, то выбирается другое её положение. При фиксированных углах a и b это достигается изменением положения основания P главной точки P в пределах средней трети отрезка [1,2]. Так, на рис. 16.4, б представлено перспективное изображение того же здания для другого положения основания P, расположенного правее. В этом случае перспективное изображение воспроизводит более достоверный по пропорциям образ объекта. Перспективные изображения на рис. 16.4 построены в масштабе 2:1 относительно масштаба ортогональных проекций.

69
à)
P |
h |
|
k |
P
á)
P |
h |
|
k |
P
Рис. 16.4
16.5. Построение перспективы объекта способом архитекторов
При построении перспективных изображений зданий, мостов, путепроводов и других сооружений, которые имеют в плане два доминирующих направления прямых линий (см. раздел 16.1), обычно используют способ архитекторов, обеспечивающий большую графическую точность и простоту построения перспективы.
ПРИМЕР 16.1. Построить в масштабе 2:1 перспективу схематизированного здания, если заданы в ортогональных проекциях (рис. 16.5) его план и фасад, горизонт h, точка зрения S, след картинной плоскости Ï1 k1, а в поле перспективы (рис. 16.6) - основание картины k, горизонт h, главная точка картины P
k1, а в поле перспективы (рис. 16.6) - основание картины k, горизонт h, главная точка картины P  h и её основание P
h и её основание P k. При этом высота горизонта на рис. 16.6 в два раза больше высоты горизонта на рис 16.5.
k. При этом высота горизонта на рис. 16.6 в два раза больше высоты горизонта на рис 16.5.

70
Построим вторичную проекцию здания - перспективу a многоугольника a[A,B,C,E,G,K,A] предметной плоскости, являющегося основанием (планом) здания. Перспектива подобного многоугольника построена на рис. 16.1, поэтому, не повторяя объяснений, относящихся к построению вторичной проекции, ограничимся рядом замечаний.
многоугольника a[A,B,C,E,G,K,A] предметной плоскости, являющегося основанием (планом) здания. Перспектива подобного многоугольника построена на рис. 16.1, поэтому, не повторяя объяснений, относящихся к построению вторичной проекции, ограничимся рядом замечаний.
Перспектива a на рис. 16.6 получена с использованием точек схода F и F
и F перспектив параллельных прямых и перспектив 1, 2, 3, 4
перспектив параллельных прямых и перспектив 1, 2, 3, 4 E , 5 картинных следов этих прямых. На комплексном чертеже (рис. 16.5) показаны проекции указанных точек с индексом “1”.
E , 5 картинных следов этих прямых. На комплексном чертеже (рис. 16.5) показаны проекции указанных точек с индексом “1”.
Поскольку перспектива здания строилась в масштабе в два раза большем масштаба ортогональных проекций, то при переносе
точек 11 , 21 , 31 , 41 |
E1 , 51 |
с плана (рис. 16.5) на ось k в перспективе |
в виде точек 1, 2, |
3, 4 |
E , 5 (рис. 16.6) расстояния от точек до |
основания P увеличивались в два раза, например,  P,1
P,1 =2x
=2x P,11
P,11 . Вершина E
. Вершина E k, из-за чего её перспектива E также лежит на оси k. В результате ширина перспективного изображения была увеличена в два раза по сравнению с планом.
k, из-за чего её перспектива E также лежит на оси k. В результате ширина перспективного изображения была увеличена в два раза по сравнению с планом.
Чтобы получить перспективу здания, имея его вторичную проекцию a , остается построить перспективы его ребер - вертикальных отрезков. Напомним, что перспективы вертикальных отрезков вертикальны. Для построения перспективы отрезка [A,T] из точки картинной плоскости 1
, остается построить перспективы его ребер - вертикальных отрезков. Напомним, что перспективы вертикальных отрезков вертикальны. Для построения перспективы отрезка [A,T] из точки картинной плоскости 1 k (1 - перспектива картинного следа прямой (A,B)) отложим вертикальный отрезок [1,T
k (1 - перспектива картинного следа прямой (A,B)) отложим вертикальный отрезок [1,T ], равный двойной высоте здания
], равный двойной высоте здания 
 в действительности расположен в картинной
в действительности расположен в картинной
Ï ). Перспектива точки T есть точка пересечения прямой
(T ,F
,F ) и вертикальной прямой, проведенной из точки A
) и вертикальной прямой, проведенной из точки A (см. рис. 15.2 и пояснения к нему). [A
(см. рис. 15.2 и пояснения к нему). [A ,T
,T ] - перспектива отрезка [A,T]. Остальные точки, находящиеся на той же высоте, строим с использованием точек схода F
] - перспектива отрезка [A,T]. Остальные точки, находящиеся на той же высоте, строим с использованием точек схода F ,F
,F и соответствующих вертикальных прямых, проведенных из вершин B , Q , K вторичной проекции a (точка Q на комплексном чертеже не показана). Перспективы другой группы вертикальных отрезков, отличных по высоте от отрезка [A,T], строятся аналогично: определяется перспектива одного из них подобно перспективе [A ,T ] отрезка [A,T], а затем используются точки схода F
и соответствующих вертикальных прямых, проведенных из вершин B , Q , K вторичной проекции a (точка Q на комплексном чертеже не показана). Перспективы другой группы вертикальных отрезков, отличных по высоте от отрезка [A,T], строятся аналогично: определяется перспектива одного из них подобно перспективе [A ,T ] отрезка [A,T], а затем используются точки схода F и F
и F . Заметим, что отрезок [E,N] расположен в картинной плоскости и его перспектива получается сразу как вертикальный отрезок [E
. Заметим, что отрезок [E,N] расположен в картинной плоскости и его перспектива получается сразу как вертикальный отрезок [E ,N
,N ], имеющий длину 2x
], имеющий длину 2x E2,N2
E2,N2 .
.
