
fel10E060
.pdf
41
занятия плоскостью  горизонтального положения
горизонтального положения 

 Ï . Поскольку вершины A и D расположены на горизонтали h9, то при вращении они будут неподвижны: A9
Ï . Поскольку вершины A и D расположены на горизонтали h9, то при вращении они будут неподвижны: A9 A9, D9
A9, D9 D9 и для поворота треугольника достаточно повернуть только вершину B.
D9 и для поворота треугольника достаточно повернуть только вершину B.
0 |
1 |
2ì |
B |
h9 |
h9 |
|
|||||
|
|
|
|


 RB
RB B6
B6 

D9 D9
D9
 C9
C9 C9
C9
A9 A9 B
A9 B
B9
Рис. 13.16
Поворот точки начинают с про-
ведения прямой B |
B6 |
B h9 - |
проекции плоскости |
B, в которой |
|
при вращении вокруг h9 |
переме- |
|
щается точка B. Точка C= |
B h9 - |
|
центр вращения точки B (C9 = B
B
 h9;
h9;
C |
h9 |
C9 |
C9), а [B,C] - радиус её |
|
вращения. |
Его величина |
RB = |
||
= |
B,C9 , |
определяется из |
прямо- |
|
угольного треугольника  BB6 C9 , построенного по катетам [B6,C9 ] и
BB6 C9 , построенного по катетам [B6,C9 ] и
[B6,B], где  B6,B
B6,B =HC-HB=3 ì.
=HC-HB=3 ì.
Когда |
ABD займет горизонтальное положение, |
радиус [B,C] |
||||||
будет проецироваться на Ï |
в натуральную величину. Поэтому |
|||||||
проекция |
B9 |
повернутой точки B |
находится на B и удалена от |
|||||
проекции горизонтали h9 на расстояние |
B9,C9 |
= RB . |
|
|||||
Величина |
A9B9D9 равна натуральной величине |
ABD. |
||||||
ПРИМЕР 13.9. Найти натуральный вид |
ABD ( |
A7 B5 D3 ), |
||||||
расположенного в плоскости |
общего положения (рис. 13.17). |
|||||||
В примере плоскость |
вращали вокруг её горизонтали h 3 , |
|||||||
проходящей через точку D. Последовательность решения: |
||||||||
1. Градуируют сторону [A,D] и строят проекции горизонталей |
||||||||
плоскости |
: |
h5 |
B5,5 и h3 |
D3 |
h3 |
h5. |
|
|
2.D3 D3 - обозначают проекции неподвижной точки D.
D3 - обозначают проекции неподвижной точки D.
3.Задают плоскости 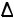 A
A  h3 и
h3 и  B
B  h3 , в которых переме-
h3 , в которых переме-
щаются точки A и B:  A
A A7
A7 
 A
A h3 и
h3 и  B
B  B5
B5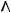
 B
B  h3.
h3.
4.C3= A
A  h3 - находят центр вращения точки A; C3
h3 - находят центр вращения точки A; C3  C3 .
C3 .
5.Находят величину  RA
RA радиуса вращения точки A.
радиуса вращения точки A.
6.Строят проекцию повернутой точки A: A3
 A,
A,  A3,C3
A3,C3 =
= RA
RA .
.
7.Определяют проекции E3  E3 точки E=(A,B)
E3 точки E=(A,B) h3 .
h3 .

42
8.Проводят проекцию (E3 ,A3 ) прямой (E,A) в повернутом положении.
9.Определяют проекцию точки B в повернутом положении:
B3= |
B |
(E3,A3). |
|
|
0 1 |
2 |
3 |
4ì |
ni |
|
|
|
A7 |
|
|
5 |
|||||
|
|
|
|
|
|
|
B |
|
||
D3 |
D3 |
|
|
|
Ê |
|
Ê6 |
h |
6 |
|
|
|
|
|
|
||||||
6 |
|
A |
|
|
|
|
6 |
|||
|
|
|
|
|
|
|
|
7 |
||
|
|
5 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
4 |
|
RA |
RK |
|
|
|
D |
8 |
|
|
|
B5 |
|
|
|
||||
|
|
|
|
|
A |
|
h9 |
|
9 |
|
|
|
|
|
|
|
|
|
|||
|
A |
C3 C3 |
|
E |
E |
A |
C9 |
B |
F9 |
F9 |
|
|
9 |
9 |
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
B |
|
|
A9 |
|
|
|
|
D |
|
|
|
|
|
|
|
|
D9 |
||
|
|
|
|
|
|
K |
|
|
||
|
|
|
E3 |
E3 |
|
|
|
|
||
|
|
|
|
|
|
|
ABD |
|
||
|
|
B3 |
2 |
4ì |
|
|
|
|
|
|
A3 |
|
0 |
|
|
Ê9 |
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
Рис. 13.17 |
|
|
Рис. 13.18 |
B9 |
|
|
||
На рис. 13.18 определяется натуральный вид  ABD, лежащего в заданной масштабом уклона n i плоскости
ABD, лежащего в заданной масштабом уклона n i плоскости  , причем отметки вершин
, причем отметки вершин  ABD неизвестны. Последовательность построений:
ABD неизвестны. Последовательность построений:
1.Проводят горизонтали плоскости  и горизонталь h 9 выбирают в качестве оси вращения.
и горизонталь h 9 выбирают в качестве оси вращения.
2.Находят проекции неподвижных точек E=(A,B)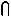 h9 и F=(B,D)
h9 и F=(B,D) h9:
h9:
E9 E9 =(A ,B ) |
h9 |
и F9 |
F9 =(B ,D ) |
h9 . |
|
|
||
3. На прямой |
(A,B) |
берут точку |
K с целой отметкой, например, |
|||||
отметкой 6: K6 =(A ,B ) |
h6 |
и строят её проекцию K9 |
в повернутом |
|||||
положении: K |
K6 |
K |
h9 ; C9 = |
K |
h9; K9 |
K |
C9,K9 = RK |
|
(радиус  RK
RK найден из прямоугольного треугольника C9K6K).
найден из прямоугольного треугольника C9K6K).
4.На прямой (E9,K9) с помощью проекций  A и
A и  B плоскостей,
B плоскостей,
вкоторых перемещаются точки A и B, находят их проекции A9 и B9. Аналогично на (B9,F9) определяют проекцию D9 вершины D.
Величина  A9B9D9 равна величине
A9B9D9 равна величине  ABD.
ABD.
Натуральный вид треугольника можно найти, определив длины трех его сторон по правилу прямоугольного треугольника.

43
Л Е К Ц И Я 14
ПЕРСПЕКТИВА
14.1. Основные понятия и определения
Перспектива (от латинского perspicere - видеть насквозь) - один из методов построения наглядных изображений пространственных предметов. Этим изображениям присущ ряд особенностей: объекты, находящиеся ближе к наблюдателю, в перспективе имеют большие размеры, чем такие же, но дальше удаленные объекты; параллельные прямые в перспективе могут пересекаться и т. д.
В начертательной геометрии перспектива - изображение предметов на поверхность по правилам центрального проецирования. Перспектива бывает линейной (строится на плоскости), панорамной (строится на цилиндрической или конической поверхностях) и купольной (строится на сфере, эллипсоиде и т. д.). В курсе рассматривается только линейная перспектива на вертикальную плоскость.
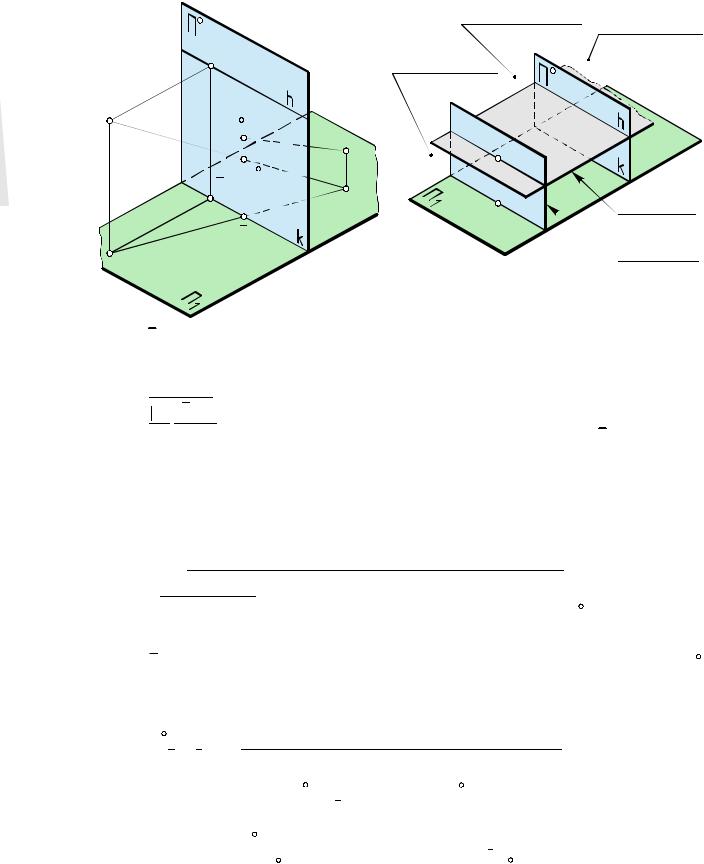
Элементы перспективного аппарата показаны на рис. 14.1 и 14 2. Ï1 - предметная плоскость: горизонтальная плоскость проекций (ПП), на которой расположены изображаемые предметы или их
ортогональные проекции.
Ï - картинная плоскость (картина): вертикальная ПП (Ï  Ï1 ), на которую осуществляется центральное проецирование.
Ï1 ), на которую осуществляется центральное проецирование.
S - центр проецирования (точка зрения).
S1 - основание точки зрения (точка стояния): горизонтальная проекция точки зрения S.
k - основание картины (ось картины): линия пересечения картинной и предметной плоскостей.
Плоскость горизонта - горизонтальная плоскость, проходящая через точку S (рис. 14.2).
Предельная (нейтральная) плоскость - плоскость, проходящая через точку зрения S параллельно картинной плоскости Ï (рис. 14.2). h - горизонт или линия горизонта: линия пересечения
плоскости горизонта и картинной плоскости Ï .
.
(S,P) - главная проецирующая прямая (главный луч): проходящий через точку зрения S перпендикуляр к плоскости Ï .
P - главная точка картины: точка пересечения главного луча с картинной плоскостью Ï .
.
|
|
44 |
|
|
|
|
Промежуточное |
Предметное |
|
|
|
пространство |
||
P |
|
пространство |
||
|
Мнимое |
|
|
|
|
|
|
|
|
|
|
пространство |
|
|
S |
A |
|
|
|
|
|
|
|
|
|
A1 |
A |
S |
|
P |
A1 |
|
|
|
|
|
Плоскость |
||
|
|
S1 |
|
|
|
A |
|
горизонта |
|
|
|
|
Предельная |
|
S1 |
|
|
|
|
|
|
|
плоскость |
|
|
Рис. 14.1 |
|
Рис. 14.2 |
|
P - основание главной точки: ортогональная проекция главной точки P на основание картины k.
 S,P
S,P - главное расстояние.
- главное расстояние.
 - горизонтальная проекция главного расстояния.
- горизонтальная проекция главного расстояния.

 - высота горизонта (точки зрения),
- высота горизонта (точки зрения),  S,S1
S,S1 =
=  P,P
P,P . Картинная и предельная плоскости (рис. 14.2) делят простран-
. Картинная и предельная плоскости (рис. 14.2) делят простран-
ство на предметную, промежуточную и мнимую части. В мнимой части и предельной плоскости объект проецирования не располагают.
На рис. 14.1 объект проецирования - точка A: (S,A) - прямая, центрально проецирующая точку A.
A =(S,A)
=(S,A)
 Ï
Ï - перспектива (первичная проекция) точки A: центральная проекция точки A на картинную плоскость Ï , получаемая при пересечении проецирующей прямой (S,A) с этой плоскостью.
- перспектива (первичная проекция) точки A: центральная проекция точки A на картинную плоскость Ï , получаемая при пересечении проецирующей прямой (S,A) с этой плоскостью.
A - основание точки A: ортогональная проекция перспективы A на основание картины k.
A1 - горизонтальная ортогональная проекция точки A.
A1 = (S,A1 )  Ï
Ï - вторичная проекция точки A: перспектива горизонтальной проекции A1 точки A.
- вторичная проекция точки A: перспектива горизонтальной проекции A1 точки A.
Перспективная (A ) и вторичная (A1 ) проекции точки расположены в проекционной связи, которую устанавливает вертикальная линия связи (A ,A1 ), перпендикулярная к оси k.
,A1 ), перпендикулярная к оси k.
Перспектива A и вторичная проекция A1 точки A однозначно задают положение точки A в пространстве, делая чертеж обратимым.

45
Мысленно уберите точку A на рис. 14.1 и подумайте, как по проекциям A и A1 можно установить положение точки A.
Обычно изображения, построенные в плоскостях Ï1 и Ï (рис. 14. 1), задают раздельно (рис. 14.3). На плане - виде сверху на пред- метную плоскость Ï1 (рис. 14.3,а) показаны ось k, точки S1, P, A1, A.
В перспективе - виде спереди на картину Ï |
видны прямые k, h и |
||||||
точки P, P, A , A1 , A. Общими элементами плана и перспективы |
|||||||
являются основание картины k с точками P и A |
на нем. |
|
|||||
à) Ï1 |
A1 |
|
á) Ï |
P |
h |
Прямоугольники, |
|
|
|
|
|||||
|
|
|
|
A |
ограничивающие |
план и |
|
|
|
|
|
перспективу на рис. 14.3, |
|||
|
|
|
|
|
|||
|
|
|
|
A1 |
устанавливают связь этих |
||
P |
A |
k |
P |
A |
k изображений с изображе- |
||
|
|
|
|
|
ниями отсеков |
плоскос- |
|
|
|
|
|
|
тей Ï1 и Ï на рис. 14.1 и не |
||
|
|
|
|
|
являются обязательными. |
||
|
S1 |
|
Рис. 14.3 |
|
|
|
|
По плану (рис. 14.3,а) и перспективе (рис. 14.3,б) можно опре- |
|||||||
делить |
положение |
точки зрения |
S относительно картинной Ï и |
||||
предметной Ï1 плоскостей: от Ï |
точка S удалена на расстояние |
||||||
S1 ,P , а от Ï1 |
- на высоту горизонта P,P . |
|
|
||||
14.2. Построение прямых линий в перспективе
На рис. 14.4 изображены прямые общего и частного положений. Прямыми общего положения в перспективе считаются прямые, не параллельные и не перпендикулярные плоскостям Ï1 и Ï ; пря-
; пря-
мые, не принадлежащие Ï1 и Ï ; прямые, не проходящие через точку зрения S и точку стояния S1. На рис. 14.4 прямые общего положения - это прямые a и b.
Прямые частного положения: g, t, l, c - горизонтальные прямые, параллельные Ï1 , из которых прямые l и t перпендикулярны к плоскости Ï и называются главными; q - вертикальная прямая (q  Ï1); c, e - фронтальные прямые, параллельные плоскости Ï ; s, p - прое- цирующие прямые, проходящие через центр проецирования S.
Ï1); c, e - фронтальные прямые, параллельные плоскости Ï ; s, p - прое- цирующие прямые, проходящие через центр проецирования S.

|
|
46 |
|
|
q |
l |
t |
|
|
|
|
|
||
|
|
|
|
|
g |
a |
s |
p |
p |
s |
|
|||
|
|
|
|
|
b |
a1 |
e |
|
S |
q1 |
|
c |
|
|
b1 |
e1 |
c1 |
|
|
|
|
p1 |
||
|
|
|
s1 |
|
|
|
|
S1 |
|
|
|
|
|
Рис. 14.4
К горизонтальным относят также прямые, расположенные в предметной плоскости Ï1 .
В общем случае прямая при центральном проецировании проецируется в прямую. Проецирующие прямые проецируются на картину в точки (на рис. 14.4 точки s и p
и p - проекции прямых s и p).
- проекции прямых s и p).
14.2.1. Перспективы прямых общего положения и горизонтальных прямых произвольного относительно картины направления
Введем ряд понятий и определений. Проецирующая плоскость - плоскость, проходящая через точку зрения S. Картинный след прямой или начало прямой - точка пересечения прямой с картиной. Картинный след плоскости - линия пересечения плоскости с картиной. Примем, что каждая прямая имеет бесконечно удаленную (несобственную) точку - точку, в которой прямая пересекается с параллельными ей прямыми. Совокупность несобственных точек прямых плоскости составляет несобственную прямую плоскости. По этой прямой плоскость пересекается с параллельными ей плоскостями.
Центральная проекция прямой есть линия пересечения картинной плоскости Ï с плоскостью, проецирующей прямую, - плоскостью, заданной точкой зрения S и проецирующей прямой. Такое задание проецирующей плоскости не удобно для построения перспективы прямой.
с плоскостью, проецирующей прямую, - плоскостью, заданной точкой зрения S и проецирующей прямой. Такое задание проецирующей плоскости не удобно для построения перспективы прямой.
На рис. 14.5 плоскость S, проецирующая прямую a, задана прямыми a и f, где f - вспомогательная проецирующая прямая: f S, f
S, f 
 a. В этом случае перспективу a
a. В этом случае перспективу a =S
=S Ï
Ï определяют две точки: A
определяют две точки: A A =
A =
=a |
Ï - картинный след прямой, совпадающий с его перспективой, и |
F =f |
Ï - перспектива несобственной точки прямой F=a f. |

|
|
|
47 |
|
|
|
|
|
|
|
a |
|
F |
|
a |
|
|
|
|
|
|
|
|
f |
f |
F |
a1 |
|
|
|
1 |
|
|
||
|
|
|
A A |
|
a1 |
|
|
F |
|
|
|
|
|
|
|
|
|
S |
|
|
|
|
h |
S1 |
|
|
|
|
|
|
|
A A1 |
k |
Рис. 14.5 |
|
|
|
|
|||
Рассмотрим построение центральной проекции прямой a (рис. 14.6,б) по её комплексному чертежу (рис. 14.6,а), на котором заданы прямая a (a1 ,a2), центр S (S1 ,S2), картинная плоскость Ï (Ï 1 ) и горизонтальная проекция k1  Ï1 основания картины k. В примере
Ï1 основания картины k. В примере
Ï
 Ï2 и Ï1
Ï2 и Ï1
 x1
x1 2. Выполним на рис. 14.6,а следующие построения:
2. Выполним на рис. 14.6,а следующие построения:
1.Через центр S проведем вспомогательную прямую f
 a:
a:
f1 S1 f1 a1 и |
f2 S2 f2 a2 . |
2. Найдем ортогональные проекции A1,A2 картинного следа прямой A =a  Ï
Ï и F1,F2 перспективы несобственной точки F
и F1,F2 перспективы несобственной точки F =f
=f Ï
Ï :
:
A1 =a1 k1 , A2 |
a2 и F1 =f1 |
k1 , F2 |
f2. |
|
|
|
|||
|
à) |
|
a2 |
|
|
|
á) |
|
|
F2 |
|
|
|
|
F |
a |
|
A |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
f2 |
S2 |
|
A2 |
F1 |
|
P |
|
h |
|
|
|
|
|
|
|
a1 |
|
||
|
|
|
|
|
|
|
k |
||
x1 2 |
|
|
a1 |
|
|
|
|
|
|
|
|
|
k1 Ï1 |
F |
P |
|
A1 A |
||
F1 |
|
P1 |
|
|
|
|
|
|
|
|
|
A1 |
|
Рис. 14.6 |
|
|
|||
|
f1 |
|
|
Когда Ï |
Ï2 , центральная проекция |
||||
|
|
S1 |
[A ,F ] отрезка [A,F] прямой a проецируется |
||||||
|
|
на |
Ï2 |
в натуральную величину и соответ- |
|||||
|
|
|
|||||||
ствует отрезку [A2,F2]. Но обычно плоскости |
Ï и Ï2 не параллель- |
||||||||
ны и перспектива строится на специальном поле перспективы. Сформируем это поле, задав его исходные элементы (рис. 14.6, б):

48
-на отведенном месте чертежа проведем основание картины k;
-проведем горизонт h 
 k, расстояние между h и k равно высоте
k, расстояние между h и k равно высоте
горизонта  S,S1
S,S1  - на комплексном чертеже это
- на комплексном чертеже это  S2,x1
S2,x1 2
2  ;
;
- зададим главную точку картины P  h и её основание точку P
h и её основание точку P k так, чтобы точка P была примерно в центре изображения. Перенесем в это поле точки A и F с комплексного чертежа:
k так, чтобы точка P была примерно в центре изображения. Перенесем в это поле точки A и F с комплексного чертежа:
1. На основании картины k отложим от точки P отрезки [P,A] и
[P,F]:  P,A
P,A =
= P1 ,A1
P1 ,A1 и
и  P,F
P,F =
= P1 ,F1
P1 ,F1  .
.
2.Из точек A и F проведем перпендикуляры к основанию k.
3.По комплексному чертежу найдем высоты точек A и F соот-
ветственно  A2, x1
A2, x1 2
2  и
и  F2,x1
F2,x1 2
2  .
.
4.Отложим эти высоты на перпендикулярах от точек A и F и
найдем точки A и F
и F :
:  A,A
A,A
 =
= A2,x1
A2,x1 2
2  и
и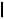 F,F
F,F
 =
= F2,x1
F2,x1 2
2  .
.
5.Проведем прямую a  A ,F : a - перспектива прямой a.
A ,F : a - перспектива прямой a.
Для задания прямой a необходимо её перспективу a дополнить вторичной проекцией a1 - перспективой проекции a1 . Проекция a1 подобно перспективе a проходит через точки A1 =a1
дополнить вторичной проекцией a1 - перспективой проекции a1 . Проекция a1 подобно перспективе a проходит через точки A1 =a1 
 Ï
Ï и F1=f
и F1=f Ï
Ï ,
,
где f - проецирующая прямая: f |
S f |
a1 (рис. 14.5). Поскольку |
|
a1 |
Ï1, то, во-первых, точка A1 |
k и A1 |
A, а, во-вторых, прямая |
f |
Ï1 и точка F1 h: F1 =(F,F ) h (рис. 14.5 и 14.6,б). Таким образом, |
||
одна характерная точка вторичной проекции прямой всегда принадлежит оси k, а вторая - горизонту h.
Так как через точку можно провести одну прямую, параллельную данной, то каждая прямая имеет только одну несобственную точку. Поэтому все прямые, параллельные между собой, пересекаются в одной несобственной точке F. Их перспективы строятся с помощью одной параллельной им проецирующей прямой f  S и проходят через точку F =f
S и проходят через точку F =f  Ï
Ï - перспективу точки F. Вывод: перспективы параллельных прямых пересекаются в точке F =f
- перспективу точки F. Вывод: перспективы параллельных прямых пересекаются в точке F =f  Ï
Ï , называемой точкой схода перспектив параллельных прямых данного направления или точкой схода прямых (прямой). У каждого направления параллельных прямых своя точка схода.
, называемой точкой схода перспектив параллельных прямых данного направления или точкой схода прямых (прямой). У каждого направления параллельных прямых своя точка схода.
При построении перспективы горизонтальных прямых проходящая через S вспомогательная прямая f 
 Ï1 . Поэтому точки схода горизонтальных прямых принадлежат горизонту h. Следовательно, перспектива и вторичная проекция горизонтальной прямой пересе- каются в общей точке схода на горизонте h.
Ï1 . Поэтому точки схода горизонтальных прямых принадлежат горизонту h. Следовательно, перспектива и вторичная проекция горизонтальной прямой пересе- каются в общей точке схода на горизонте h.

49
Рассмотрим построение перспектив параллельных горизон-
тальных прямых a |
и b |
произвольного относительно картины |
Ï |
|||||||||
положения, из которых b |
Ï1. На комплексном чертеже (рис. 14.7,а) |
|||||||||||
были заданы прямые a |
(a1 ,a2), b (b1 ,b2), точка зрения S (S1 ,S2 ), |
|||||||||||
картинная плоскость Ï (Ï 1 ) |
и проекция основания картины k1 |
Ï1 . |
||||||||||
Последовательность построения перспектив: |
|
|
|
|
||||||||
1. |
Находим проекцию F1 =f1 Ï |
несобственной точки F прямых a |
||||||||||
и b (прямая f |
S и f |
a |
b), проводя f1 |
S1 |
f1 a1 |
b1 |
(рис. 14.7, а). |
|||||
2. |
Ищем проекции картинных следов A и B |
прямых a и b: |
||||||||||
A1 =a1 |
Ï1 ; B1 =b1 |
Ï1 ; A2 |
a2 ; B2 |
|
b2 (рис. 14.7,а). |
|
|
|||||
3. |
Строим проекцию P1 |
главной точки P картины: (S1 ,P1) |
k1 . |
|||||||||
4. |
Формируем поле перспективы (рис. 14.7,б), проводя k и h k |
|||||||||||
(расстояние между |
k |
и |
h равно |
S2, x1 2 |
- высоте горизонта) и |
|||||||
задавая главную точку P |
h. |
|
|
|
|
|
|
|
||||
5. |
Переносим в поле перспективы (рис. 14.7,б) точку схода F |
|||||||||||
на горизонт h ( P,F |
= P1 ,F1 ), а точки P1 , A1 |
и B1 |
- на ось k в виде |
|||||||||
точек P, A и B |
([P,P] |
k; P,A = P1 ,A1 |
и |
P,B = P1 ,B1 |
). |
|
|
|||||
6. |
Отмечаем вторичные проекции точек A и B: A1 |
A и B1 |
B |
|||||||||
(A1 k |
B1 |
k, поскольку точки A и B лежат в плоскости Ï ). |
|
|||||||||
7.Строим вторичные проекции прямых: a 1 A1 ,F
A1 ,F и b1
и b1 B1,F
B1,F .
.
8.Проводим перпендикуляр к основанию k из точки A1  A и
A и
откладываем на нем высоту прямой |
a, получая точку A |
( A ,A = |
||
= A2,x1 2 ). Высота прямой b равна 0 и B |
B1 . |
A ,F . |
Так как |
|
9. Проводим перспективу a |
прямой |
a : a |
||
b |
Ï1 , то b b1 . |
à) |
A2 |
|
S2 |
B2
x1 2 k1
2 k1 Ï1
Ï1  A1
A1
P1  B1 S1 f1
B1 S1 f1
a2
b2
a1
b1
 F1
F1
|
A |
á) |
|
h |
P |
a |
F |
|
|||
|
|
a1 |
|
k |
|
|
|
A1 A |
P |
|
F |
B B1
B1 B
B b1
b1 b
b
Рис. 14.7

50
О расположении прямой в пространстве можно судить по положению её точки схода F на картине. Если F выше горизонта h, то прямая восходящая (прямые a и f на рис. 14.5) - её точки при удалении от наблюдателя поднимаются. Если точки F ниже h, то прямая нисходящая. Если точка F  h, то прямая горизонтальная (прямая a на рис. 14.7, б). Если прямая не имеет точки схода, то она параллельна картине Ï (проецирующая прямая f
h, то прямая горизонтальная (прямая a на рис. 14.7, б). Если прямая не имеет точки схода, то она параллельна картине Ï (проецирующая прямая f  S
S  f
f 
 Ï ).
Ï ).
Примем, что в обозначении точки схода F верхний индекс “
верхний индекс “ “ может не даваться, а при нескольких точках схода в качестве верхнего индекса будут указываться штрихи: F , F , ... .
“ может не даваться, а при нескольких точках схода в качестве верхнего индекса будут указываться штрихи: F , F , ... .
В заключении можно сделать следующие выводы:
1.Перспектива и вторичная проекция точки находятся на одной линии связи, перпендикулярной основанию картины k.
2.Перспективы параллельных между собой прямых пересекаются, т. е. имеют общую точку схода.
3.Точки схода вторичных проекций прямых всегда принадле-
жат горизонту h.
4. Точки схода параллельных горизонтальных прямых, включая прямые предметной плоскости, расположены на горизонте h. Поэтому перспектива и вторичная проекция горизонтальной прямой имеют общую точку схода на горизонте h.
5. Прямые предметной плоскости Ï1 пересекаются с картинной плоскостью Ï в точках, расположенных на оси картины k.
6. Вторичная проекция прямых предметной плоскости и их перспектива совпадают.
14.2.2. Перспективы прямых предметной плоскости
Предварительно договоримся о следующих условностях:
1. Допускается в обозначении образов на плане, кроме обозначения точки стояния S1 , не указывать подстрочный индекс “1”, а основание главной точки на плане обозначать P.
2.Совпадающие первичную и вторичную проекции образов допускается обозначать только как перспективу.
3.Точки пересечения прямой и её перспективы с осью k допускается обозначать арабскими цифрами без индексов.
