fel10E060

ПРИМЕР 13.4. Построение линий пересечения поверхностей откосов.

На рис. 13.6 дана горизонтальная строительная площадка с отметкой 15 и аппарель, выполненные в насыпи, так как они расположены выше окружающей плоской горизонтальной местности, имеющей отметку 12.

Аппарель - наклонный прямолинейный или криволинейный въезд или съезд (участок дороги с продольным уклоном).

Горизонтальная площадка задана на чертеже проекцией её контурной линии (бровки), состоящей из половины дуги окружности и отрезков прямых линий, а аппарель - проградуированной проекцией a её бровки. Уклон откосов насыпи на участке левее точки B i=1:1,5, на остальных участках сооружения уклон i=1:1.

Поверхности откосов насыпи на участках между точками A и B, C и D, D и E плоские, между точками B и C имеют коническую форму, на аппарели - ограничены поверхностью равного уклона, направляющей которой является бровка a. Как уже отмечалось, линия пересечения поверхностей определяется точками пересечения их одноименных горизонталей. Поэтому к построению линий пересечения поверхностей смежных откосов приступают, осуществив их градуирование (см. раздел 12.6). После этого, например, проекция k линии k пересечения плоского откоса с поверхностью равного уклона проводится через точки пересечения проекций соответствующих горизонталей этих поверхностей.

Плоскость, не проходящая через вершину конической поверхности, пересекает её по кривой второго порядка (рис. 13.7). Плоскость и коническая поверхность пересекаются по эллипсу, если уклон плоскости меньше уклона конической поверхности (a b); по параболе, если уклон плоскости и конической поверхности одинаковы (a = b); по гиперболе, если уклон плоскости больше уклона конической поверхности (a b). Соответственно плоский откос

E

D

Линии пересечения смежных откосов

Эллипс B

Поверхность земли с отметкой 12

Рис. 13.6

à (i=1:1) пересекает коническую поверхность по параболе, а плоский откос

(i=1:1,5 ) - по эллипсу (рис. 13.6). Поскольку плоские откосы Ã и

Ôимеют одинаковый уклон, то прямая, проекция их линии пересечения,

33

цию линии пересечения откосов с горизонтальной (плоской) поверхностью окружающей местности, имеющей такую же отметку. Эта линия пересечения называется подошвой откосов насыпи и является здесь границей земляных работ.

13.1.3. Решение 1ГПЗ (3-й случай)

В 3-м случае 1ГПЗ пересекаются непроецирующие линия и поверхность. Общий алгоритм решения задачи:

1.Линия заключается во вспомогательную поверхность: прямая линия заключается во вспомогательную плоскость, кривая линия - во вспомогательную цилиндрическую поверхность.

2.Строится линия пересечения данной поверхности и вспомогательной.

3.Искомые точки - точки пересечения данной линии и построенной.

При решении 1ГПЗ-3 следует проградуировать поверхность (если она не проградуирована), а при необходимости и линию.

34

Для определения видимости прямой (A,B) относительно плоскости Ï рассмотрим конкурирующие точки A и QS (A9 Q ). Точка A прямой имеет отметку 9, а точка Q плоскости - отметку меньше 5 (учитывая уклон плоскости S). Поэтому участок прямой (A,K] расположен над плоскостью S и виден относительно Ï .

Чтобы построить точку K пересечения прямой (A,B), заданной проекцией (A2,B6), с топографической поверхностью W (рис. 13.10,а), градуируем прямую (эти построения на рисунке не показаны) и заключаем её в плоскость общего положения Ã. Для этого через точки A2, 3, 4, 5, B6 проводим проекции параллельных горизонталей в произвольном направлении, но таком, чтобы они пересекали проекции горизонталей поверхности W в пределах чертежа. Отметив точки пересечения проекций одноименных горизонталей плоскости Ã и поверхности W, соединим их плавной кривой k,

кривой p, представленной проекцией p и проекциями градуирующих её точек с отметками 4, 5, 6 и 7 ì, с топографической поверхностью W. Зададим цилиндрическую поверхность F, направляющей которой является линия p, а образующими - параллельные горизонтали, проходящие через градуирующие её точки. Направление горизонталей произвольное, но такое, чтобы проекции горизонталей поверхностей F и W пересекались в пределах чертежа. Через точки пересечения проекций одноименных горизонталей этих

13.10,б определялась с помощью конкурирующих точек C и D, из которых точка C принадлежит соответственно прямой или кривой, а точка D - поверхности W. На обоих рисунках отметка точки C линии меньше отметки точки D, расположенной на горизонтали поверхности W (так, на рис. 13.10, а отметка точки C прямой (A,B) лежит в пределах (2-3) ì, отметка же точки D поверхности равна 6). Поэтому участки прямой (A,B) и кривой p, на которых бралась точка C, относительно Ï не видны. Точка K - граница видимости.

36

13.2 Метрические задачи

Метрические задачи подробно рассмотрены в первой части пособия. Напомним, что к метрическим относятся задачи на определение расстояний, площадей, углов и т. д. Решение этих задач основывается на решении двух задач, условно называемых основными метрическими задачами (ОМЗ).

13.2.1. Основные метрические задачи

1ОМЗ - задача на перпендикулярность прямой и плоскости, решаемая на чертеже с использованием признака перпендикулярности прямой и плоскости, а также теоремы о проецировании прямого угла. Согласно этой теореме проекция перпендикуляра к плоскости перпендикулярна проекциям её горизонталей (парал- лельна масштабу уклона).

куляра к плоскости обратно пропорциональны, причем отметки перпендикуляра убывают в направлении, обратном убыванию отметок плоскости (рис. 13.11). Естественно обратно пропорциональны и интервалы плоскости (интервал её линии ската) l ïë (l) и перпендикуляра к ней lïåð (la): lïë=1/l ïåð .

Пусть требуется из точки K (K4 ) плоскости , заданной мас-

дикуляра, проходящей через проекцию K4 точки K параллельно

37

n i , определению интервала la перпендикуляра и градуированию a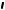. Интервал la можно подсчитать по формуле или найти графи-

чески следующим образом:

видимость перпендикуляра относительно Ï .

2ОМЗ - задача на определение длины отрезка (расстояния между двумя точками). Решение 2ОМЗ уже было рассмотрено. Длину отрезка ищут по правилу прямоугольного треугольника (пример 11.1) или при построении профиля отрезка (рис. 11.8 - 11.11), основанном по существу на реализации этого правила.

13.2.2. Определение расстояния от точки до плоскости

Расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, проведенного из точки на плоскость. Это расстояние ищется согласно такому алгоритму:

1.Через точку проводят перпендикуляр к плоскости (1ОМЗ).

2.Ищут точку пересечения перпендикуляра и плоскости (1ГПЗ).

3.Определяют длину отрезка перпендикуляра (2ОМЗ).

ПРИМЕР 13.6. Найти расстояние от точки M(M 8 ) до плоскости , заданной масштабом уклона n i (рис. 13.13).

38

Последовательность выполнения примера:

1.Строится прямая aM a :

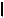-проводят проекцию a M8, a n i ;

-с помощью BCD, построенного по интервалу l плоскости и отрезку [C,N] длиной 1ì, находят интервал la перпендикуляра a;

ние M,S=M,K.

На рис. 13.14 найдено расстояние от точки M (M10) до плоскости , заданной точками A, B и D. Сначала была проградуирована плоскость . Для этого соединили точки B6 и D9, проградуировали отрезок [B6 ,D9 ], разделив его на 3 части, через точку A7 и проекцию точки отрезка [B,D] с отметкой 7 провели проекцию h7 горизонтали плоскости, после чего параллельно h7 построили проекции других её горизонталей. Затем перпендикулярно проекциям горизонталей провели масштаб уклона ni плоскости и нашли её интервал l . Далее повторяется ход решения примера 13.6.

13.2.3. Определение расстояния от точки до прямой

Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, проведенного из точки на прямую. Алгоритм решения этой задачи:

1.Через точку перпендикулярно прямой проводят плоскость

(1ОМЗ).

2.Ищут точку пересечения прямой и плоскости (1ГПЗ).

3.Определяют длину отрезка между данной точкой и построенной точкой пересечения (2ОМЗ).

40

Последовательность выполнения примера:

1.Задают плоскость M, a:

-градуируют проекцию a прямой a и определяют её интервал la,

если a не градуирована и интервал la не задан (процесс градуирования на рис. 13.15 не показан);

-построив прямоугольный QCG по интервалу la прямой и отрезку [C,N] длиной 1ì, определяют интервал l плоскости;

-строят масштаб уклона n i - градуированную проекцию линии ската плоскости , проходящую через точку M9 параллельно проекции a.

2. Ищут точку K=a :

- проекциями h4Ã и h7Ã параллельных горизонталей задают вспомогательную плоскость Ã, проходящую через прямую a;

ni проекции горизонталей плоскости );

-находят проекцию K=b a точки K=a 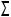и её отметку HÊ5,4 ì.

3.Определяют длину M,K отрезка [M,K], равную длине M,K его

профиля [M,K], который строится по правилу прямоугольного треугольника как в примере 13.6.

13.2.4. Определение натурального вида плоской фигуры

В проекциях с числовыми отметками эта задача обычно решается способом вращения плоскости фигуры вокруг её горизонтали до положения уровня Ï , когда фигуры плоскости проецируются на Ï в натуральную величину. Все точки повернутой плоскости имеют отметку горизонтали, являющейся осью вращения. При вращении фигуры вокруг горизонтали её точки перемещаются по окружностям, плоскости которых перпендикулярны горизонтали, а центры находятся на ней. Поэтому на Ï траектории точек вращаемой фигуры проецируются в отрезки, перпендикулярные проекции горизонтали плоскости . Исключение - точки оси вращения, остающиеся неподвижными. Под обозначением повернутого ГО и его проекции наносят черту.

ПРИМЕР 13.8. Найти натуральный вид ABD (A9 B6 D9 ) (рис.13.16).

Чтобы определить натуральный вид ABD, его поворачивают вокруг горизонтали плоскости треугольника с отметкой 9 (h9) до