
fel10E060
.pdf
21
Косой (наклонный) открытый геликоид на рис. 12.11 является поверхностью равного уклона, направляющая которой представляет собой цилиндрическую винтовую линию k с вертикальной осью j. Формула этого геликоида имеет вид:
 {l(k)(li
{l(k)(li k)}. Согласно ей прямолинейная образующая li при образовании поверхности движется, касаясь направляющей k во всех её точках (обкатывая её). На рис. 12.11 показаны три образующие косого открытого геликоида, одна из которых обозначена li. Иногда указанный геликоид называют эвольвентным, так как он пересекается плоскостью, перпендикулярной оси j винтовой линии, по эвольвенте. Проекции горизонталей эвольвентного геликоида строят, как показано на рис. 12.9, а.
k)}. Согласно ей прямолинейная образующая li при образовании поверхности движется, касаясь направляющей k во всех её точках (обкатывая её). На рис. 12.11 показаны три образующие косого открытого геликоида, одна из которых обозначена li. Иногда указанный геликоид называют эвольвентным, так как он пересекается плоскостью, перпендикулярной оси j винтовой линии, по эвольвенте. Проекции горизонталей эвольвентного геликоида строят, как показано на рис. 12.9, а.
Прямолинейные образующие прямого закрытого геликоида Ô{t(k,j)(ti k; ti
k; ti j; ti
j; ti j)} пересекают цилиндрическую винтовую линию
j)} пересекают цилиндрическую винтовую линию
k и под прямым углом её ось j. |
0 |
2 4ì |
|
t25 |
5 |
||
Поскольку |
ось j у используемого в |
j |
5 |
||||
дорожном |
строительстве геликоида |
|
k |
|
4 |
|
|
занимает проецирующее положение, |
|
b |
|
||||
1 |
|
4 |
|||||
то его образующие являются горизон- |
|
|
3 |
||||
t0 |
0 |
|
|
||||
талями. Три образующие геликоидаÔ, |
|
2 |
|
|
|||
одна их которых ti , изображены на |
|
1 |
3 |
a |
|||
0 |
|
|
|||||
рис. 12.11. |
Для лучшего понимания |
1 |
2 |
|
|
||
образования |
поверхности дорожного |
|
|
|
|||
полотна на |
съезде на рис. 12.12 в |
|
Рис. 12.12 |
|
|||
проекциях |
с |
числовыми отметками |
|
|
|||
|
|
|
|
|
|||
дан основной чертеж отсека геликоида, линиями обреза которого являются винтовые линии b, a и образующие t1, t2. Образующие геликоида, имеющие высоту 0, 1, 2, 3, 4, 5 ì, градуируют отсек его поверхности и дуги винтовых линий b и a.
12.5. Топографическая поверхность
Топографическая поверхность является геометрическим образом Земли и относится к незакономерным поверхностям, не имеющим геометрического закона образования. Поэтому топографическую поверхность (рельеф местности) представляют дискретным каркасом её горизонталей (планом местности).

22
Эти горизонтали являются результатом сечения поверхности земли горизонтальными плоскостями, взятыми по высоте через одинаковые расстояния, называемые шагом сечения. Шаг сечения зависит от масштаба чертежа и рельефа местности, в учебных работах он равен 1 м.
На рис 12.13 в проекциях с числовыми отметками показан отсек топографической поверхности. Анализ формы горизонталей и
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
12 |
|
|
|
|
|
|
|
12,7 |
11 |
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
7 |
|
11,4 |
|
|
|
|
|
|
6,5 |
10 |
11 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
5 |
9 |
|
|
|
|
8 |
0 |
20 |
40 |
60ì |
Бергштрих |
|
|
|
|
Рис. 12.13
их числовых отметок показывает, что на чертеже изображена возвышенность (неровность земли, расположенная выше окружающей местности) с двумя вершинами, отметки которых равны 11,4ì и 12,7ì. Боковые поверхности возвышенности называют склонами, а возвышенность между двумя вершинами - седловиной. Неровность земли, расположенную ниже окружающей местности, называют котловиной (впадиной), низшую часть котловины - дном, её боковые поверхности - щеками. Каждую пятую горизонталь рекомендуется обводить более толстой линией.
При необходимости на чертеже штриховой линией изображают промежуточные горизонтали, расстояние между которыми по высоте равно половине или четверти шага сечения. Такие горизонтали называют соответственно полугоризонталями (полугоризонталь с отметкой 6,5ì на рис. 12.13) или четвертными.
Бергштрихи, указывающие направление ската поверхности, позволяют быстрее оценить форму рельефа местности по чертежу.
Любая линия на топографической поверхности градуируется горизонталями этой поверхности. На рис. 12.14 проекцию k линии k градуируют точки D16, E15 и F14. Обычно дуга кривой линии топографической поверхности, соединяющая точки двух смежных горизонталей, аппроксимируется отрезком прямой. Так, проекцию k
линии k градуируют точки D16, E15 и F14. Обычно дуга кривой линии топографической поверхности, соединяющая точки двух смежных горизонталей, аппроксимируется отрезком прямой. Так, проекцию k

23 |
|
|
|
|
|
дуги k топографической поверхности |
0 |
1 |
2ì |
|
|
аппроксимируют отрезки [F14 ,E 15 ] и |
|
|
|
|
|
[E15 ,D16 ]. При этом считается, что |
k |
|
|
|
|
уклон и интервал дуги кривой равен |
D16 |
|
|
||
уклону и интервалу аппроксимирую- |
|
B |
|||
16 |
|
|
|||
щего отрезка. |
|
|
B15 |
|
|
Отметку точки M линии k то- |
|
|
A |
||
пографической поверхности, проек- |
15 |
E15 |
A? |
||
|
|||||
ция M? которой расположена между |
|
M? |
|
C14 C |
|
проекциями горизонталей, определя- |
14 |
F14 |
|
|
|
ют приближенно (см. определение |
|
Рис. 12.14 |
|||
отметки точки M на рис. 11.18). |
|
|
|||
Пусть требуется найти отметку точки A топографической |
|||||
поверхности, проекция A? которой задана. Проведем через A? произ- |
|||||
вольный отрезок [B15 ,C14], концы B15 |
и C14 |
которого расположены на |
|||
проекциях ближайших горизонталей. Из положения проекции точки A?
ихарактера рельефа окружающей местности следует, что отметка точки A лежит в пределах 14...15ì. Построим профиль [B,C] отрезка [B,C]
инайдем на нем проекцию A точки A : A [B,C]. Чтобы определить, на какую величину отметка точки A больше отметки 14ì точки C, доста-
[B,C]. Чтобы определить, на какую величину отметка точки A больше отметки 14ì точки C, доста-
точно при построении профиля [B,C] отложить от точки B15 в направлении, перпендикулярном [B15,C14], превышение отрезка [B,C], рав- ное 1ì. Измерив с учетом вертикального масштаба отрезок [A? ,A], получаем, что его длина примерно соответствует 0,4ì и отметка точки A равна 14,4ì. На рис. 12.14 вертикальный масштаб равен линейному (горизонтальному) масштабу плана.
На рис. 12.14 показано также приближенное построение проекций промежуточных горизонталей при относительно спокойном изменении рельефа. Для этого между проекциями горизонталей с отметками 15 ì и 16 ì проведено несколько отрезков, разделенных на равные части (в нашем случае на 4). Соединяя соответствующие точки деления отрезков, получают проекции четвертных горизонталей с отметками 15,25; 15,5 и 15,75 ì .
Крутизна топографической поверхности в данной точке равна углу наклона касательной к линии ската в этой точке. Соответственно уклон линии ската в данной точке поверхности определяет уклон поверхности в той же точке. Линия ската топографической поверхности перпендикулярна её горизонталям.

24
Линией равного уклона называется такая линия на топографической поверхности, интервал которой на всем её протяжении является постоянной величиной. Существует несколько способов приближенного построения линии ската и линии равного уклона топографической поверхности [4], [6].
12.6. Градуирование (задание) поверхностей откосов земляного полотна автомобильной дороги
Откосы земляного полотна автомобильной дороги ограничены поверхностями равного уклона. Их направляющей является бровка земляного полотна дороги. Бровка земляного полотна (дороги) - линия пересечения земляного полотна с откосом насыпи, выемки (при отсутствии кювета) или кювета. Поверхности откосов задаются на чертеже проекциями их горизонталей, отметки которых для насыпи в направлении от бровки убывают, а для выемки возрастают. На рис. 12.15 заданы поверхности откосов с уклоном i=1:1 (l=1 ì) для различных участков дорог, проходящих в выемке без кюветов.
1. Прямолинейный участок, продольный уклон i=0 (рис. 12.15, а) В этом случае бровка a дороги - горизонтальная прямая, а поверхность откосов - наклонная плоскость. Проекции её горизонталей параллельны проекции a5 и расположены друг от друга на рас-
стоянии, кратном интервалу плоскости.
2. Прямолинейный участок, продольный уклон i=0 (рис. 12.15, б) Здесь бровка a - прямая общего положения, поверхность откосов - наклонная плоскость, проекции горизонталей которой строятся с
помощью вспомогательных конусов (рис. 12.10,б и пояснения к нему). 3. Криволинейный участок, продольный уклон i=0
Если бровка a - дуга окружности или близкой к ней по форме кривой, то поверхность откоса - это поверхность прямого кругового конуса. Проекции её горизонталей являются концентрическими окружностями с центром в проекции вершины конуса (рис. 12.15,в). Для откосов насыпи вершина конуса направлена вверх, а для откосов выемки - вниз.
Если бровка a - некая горизонтальная кривая (рис. 12.15, г), то проекции горизонталей поверхности равного уклона представля- ют собой эквидистантные кривые, которые проводят касательно к проекциям горизонталей вспомогательных конусов (рис. 12.9, б и пояснения к нему). Также строят проекции горизонталей откосов в случае, когда бровка a - дуга окружности, центр которой недоступен.

à)
â)
|
25 |
|
|
|
Ось дороги |
á) |
Ось дороги |
|
|
+5,00 |
a5 |
|
|
|
|
|
|
a |
|
|
5 |
6 |
7 |
8 |
6
7
8
ã) |
+5,00 |
a5 |
|
|
|
|
|
D |
|
+5,00 |
B |
|
C |
|
|
|
|||
A |
|
|
|
|
a5 |
|
|
|
6
7
8
ä)
0 2 4ì
Рис. 12.15 |
8 |
|
4. Криволинейный участок, продольный уклон i=0 (рис. 12.15, д)
Здесь бровка a - пространственная кривая. Проекции горизонталей поверхности откосов также строят с использованием вспомогательных конусов (рис.12.9,а и пояснения к нему). Уже отмечалось, что если a - цилиндрическая винтовая линия, то поверхностью откосов является косой (наклонный) открытый геликоид (рис. 12.11).
26
Л Е К Ц И Я 13
ГЛАВНЫЕ ПОЗИЦИОННЫЕ И МЕТРИЧЕСКИЕ ЗАДАЧИ
13.1. Главные позиционные задачи
В первой части пособия на многокартинном комплексном чертеже уже рассматривались главные позиционные задачи (ГПЗ): 1ГПЗ - задача на пересечение линии и поверхности; 2ГПЗ - задача на пересечение поверхностей. Эти задачи решались согласно трем алгоритмам, каждый из которых соответствует одному из трех возможных случаев расположения пересекающихся геометрических образов (ГО) относительно плоскости проекций: 1 случай - оба пересекающихся ГО проецирующие; 2 случай - один пересекающийся ГО проецирующий, а второй нет; 3 случай - оба пересекающихся ГО не являются проецирующими.
Конструктивные особенности поверхностей искусственных сооружений, изображаемых в проекциях с числовыми отметками, предопределяют в основном третий, а также второй случай расположения пересекающихся ГО относительно горизонтальной плоскости Ï.
13.1.1. Решение 2ГПЗ (2 случай). Профиль поверхности
Во 2-ом случае 2ГПЗ пересекаются две поверхности, одна из которых занимает проецирующее положение. Алгоритм решения:
1.Проекция линии пересечения на чертеже задана и её только обозначают: она принадлежит основной проекции проецирующей поверхности в силу собирательного свойства этой проекции.
2.Из условия принадлежности линии пересечения непроецирующей поверхности на проекции этой линии находят и обозначают проекции точек с числовыми отметками, необходимые для задания или представления линии пересечения на чертеже. Указанные проекции точек - точки пересечения проекций горизонталей непроецирующей поверхности с проекцией линии пересечения.
Согласно алгоритму при пересечении проецирующей и непроецирующей поверхностей последнюю удобно задавать (представлять) её горизонталями.
ПРИМЕР 13.1. Построить линию пересечения плоскости общего
положения Ã( ABD) и проецирующей плоскости
ABD) и проецирующей плоскости  (
( ) (рис. 13.1). Пусть плоскости пересекаются по прямой a: a=
) (рис. 13.1). Пусть плоскости пересекаются по прямой a: a=
 Ã. Проекция
Ã. Проекция
a уже известна: a


 Ï
Ï  a
a 
 . Для задания прямой a на её
. Для задания прямой a на её

|
|
|
|
|
27 |
|
|
|
|
|
|
|
проекции a |
находят проекции |
|
|
B7 |
0 2 |
|
4ì |
|||||
точек E, F и их числовые от- |
|
|
6 |
|
|
|
|
|||||
метки: E =h |
à a , |
F |
2 |
=h à |
a , a |
|
|
5 |
|
|
|
|
4 |
4 |
|
2 |
|
|
|
|
|
|
|
||
где h4Ã, h 2Ã - |
проекции горизон- |
|
|
|
|
D |
|
|
||||
талей плоскости Ã. |
С градуи- |
|
4 |
E4 |
|
4 |
|
à |
||||
|
|
|
|
h4 |
||||||||
рования стороны |
|
|
[A,B] |
и |
3 |
|
|
|
|
|
|
|
построения проекций h4Ãи h2Ã |
|
|
F2 |
|
|
|
||||||
|
|
|
|
h |
à |
|||||||
рекомендуется начать реше- |
|
|
|
|
|
2 |
||||||
ние примера. |
|
|
|
A2 |
|
|
Рис. 13.1 |
|
|
|
||
Фигура |
сечения |
поверхности |
вертикальной |
проецирующей |
||||||||
(профильной) плоскостью называется профилем. Профиль уточняет форму участка поверхности, попавшего в секущую плоскость. При построении профиля поверхности поверхность удобно задавать горизонталями. Задача на пересечение проецирующей плоскости с непроецирующей поверхностью является составной частью задачи на построение профиля этой поверхности.
ПРИМЕР 13.2. Построить профиль p топографической поверх-
ности , соответствующий профильной плоскости |
Ï (рис. 13.2). |
|||
Сначала строится линия пересечения p= |
. Проекция p на |
|||
чертеже задана: p |
Ï |
p |
. Одновременно p , поэтому |
|
линию p пересекают горизонтали топографической поверхности,
проекции которых градуируют проекцию |
p . Таким образом, линия p |
|
представлена на чертеже проекцией |
p и |
градуирующими её |
проекциями точек с отметками 18, 19, 20, 21, 22, 22, 21, 20 и 19. |
||
Профиль топографической поверхности |
, соответствующий |
|
профильной плоскости  , - это плоская фигура, ограниченная профилем p линии p=
, - это плоская фигура, ограниченная профилем p линии p=


 .
.
Для определения координат точек профиля p в плоскости  выбирается базовая горизонталь профиля, которую называют базой (основанием) профиля и обозначают bHb . Числовая отметка Hb базовой горизонтали зависит от формы сечения, например, рельефа участка местности и инженерных сооружений на нем.
выбирается базовая горизонталь профиля, которую называют базой (основанием) профиля и обозначают bHb . Числовая отметка Hb базовой горизонтали зависит от формы сечения, например, рельефа участка местности и инженерных сооружений на нем.
Чтобы получить профиль p, плоскость S с линией p совмещают с плоскостью чертежа. При построении наложенного профиля его основание совмещают с основной проекцией плоскости S: bHb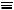 S , а при выполнении вынесенного профиля основание bHb располагают произвольно на поле чертежа. В примере базовая горизон-
S , а при выполнении вынесенного профиля основание bHb располагают произвольно на поле чертежа. В примере базовая горизон-

28

 p
p
b18(bHb) 
p
Ê
Ê
 Ê20
Ê20
Nb A
A
 A N
A N A18
A18
таль имеет отметку 18, основание профиля
b18

 и профиль p находится в проекционной
и профиль p находится в проекционной
связи с проекцией p .
.
Параллельно базе bHb (на рис. 13. 12 это b18 ) проводят другие горизонтали профиля. Расстояние между соседними горизонталями равно единице вертикального масштаба, который в отдельных случаях может отличаться от горизонтального.
В общем случае профиль p - кривая ли- ния, аппроксимирующая
точки профиля - профильные проекции градуирующих p точек. Найдем точку K профиля p с отметкой 20, которую строят по
точек. Найдем точку K профиля p с отметкой 20, которую строят по
горизонтальной координате LK и вертикальной координате HK .
Координата LK определяется берущимся с плана расстоянием LK до некой начальной точки N на p или 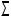 и соотношением линейного масштаба плана и горизонтального масштаба профиля. В примере N
и соотношением линейного масштаба плана и горизонтального масштаба профиля. В примере N A18 , а указанные масштабы равны и LK=LK. На базе b18 выбирают начало отсчета точку Nb и откладывают от неё по b18 координату LK , получая точку K , задающую положение точки K профиля p по его ширине (длине). На рис. 13.2 точки N и Nb находятся в проекционной связи, LA=LA=0 и Nb
A18 , а указанные масштабы равны и LK=LK. На базе b18 выбирают начало отсчета точку Nb и откладывают от неё по b18 координату LK , получая точку K , задающую положение точки K профиля p по его ширине (длине). На рис. 13.2 точки N и Nb находятся в проекционной связи, LA=LA=0 и Nb A
A .
.
Координата HK - высота точки K профиля и HK =HK -Hb, где H K - числовая отметка точки K. Отложив с учетом вертикального масштаба HK от точки K в перпендикулярном к базе b18 направлении, находят точку K профиля. В примере HK=20-18=2 ì, HA=0, A A
A .
.
Также строят |
другие точки профиля и проводят через них |
|
плавную кривую p - |
профиль линии p= |
. |

|
|
|
|
29 |
|
|
|
На рис. 13.3 построена линия пересечения k топографичес- |
|||||
0 |
2 |
4ì |
|
Ô k |
кой поверхности |
с проеци- |
|
|
|
|
C7 |
рующей цилиндрической по- |
|
|
|
|
|
верхностью Ô, заданной своей |
||
|
|
|
|
7 |
основной проекцией Ô . Линия |
|
|
B8 |
|
Ê9 |
D8 |
k представлена |
на чертеже |
|
|
|
8 |
проекцией k Ô |
и проекциями |
|
|
|
|
|
точек, в которых k пересекает- |
||
N A7 |
|
|
|
9 |
||
|
7 |
|
8 |
ся с проекциями горизонталей |
||
|
|
|
Рис. 13.3 |
топографической поверхности. |
||
13.1.2. Решение 2ГПЗ (3-й случай)
Решение 2ГПЗ в 3-м случае (пересекаются две непроецирующие поверхности) основано на положении: линия пересечения двух поверхностей есть геометрическое место точек пересечения их одноименных горизонталей (горизонталей с одинаковыми отметками). Алгоритм решения задачи следующий:
1.Градуируют пересекающиеся поверхности, строя их горизонтали, если они не заданы.
2.Строят точки пересечения одноименных горизонталей поверхностей.
3.Через построенные точки проводят линию пересечения поверхностей (её проекция градуируется проекциями точек с числовыми отметками пересечения одноименных горизонталей ).
При необходимости определяют видимость линии пересечения
ипересекающихся поверхностей относительно Ï .
ПРИМЕР 13.3. Построить линию пересечения плоскостей  , заданной
, заданной  ABD, и Ã, заданной масштабом уклона nÃi (рис. 13.4,а).
ABD, и Ã, заданной масштабом уклона nÃi (рис. 13.4,а).
Две плоскости пересекаются по прямой линии, следовательно, в примере достаточно построить две точки, принадлежащие этой
прямой. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
После градуирования плоскости (процесс градуирования на |
||||||||||||||||||
рис.13.4,а не показан) проводят проекции h6 |
|
и h4 |
её горизонталей |
||||||||||||||||
до пересечения их с проекциями h6Ã |
и h4Ã горизонталей плоскости Ã |
||||||||||||||||||
в точках E |
6 |
=h |
6 |
h à |
и F |
|
=h |
4 |
h à . Прямая |
a |
E |
6 |
,F |
- проекция |
|||||
|
|
|
|
|
6 |
4 |
|
4 |
Ã. |
|
|
|
4 |
|
|||||
линии пересечения плоскостей |
и |
|
|
|
|
|
|
||||||||||||
=h à |
Для |
|
определения |
видимости |
возьмем |
проекции |
M4 N6= |
||||||||||||
h |
6 |
конкурирующих точек M |
|
à и N |
. Точка N с отметкой 6 |
||||||||||||||
4 |
|
|
|
выше точки M с отметкой 4 плоскости Ã. Поэтому часть |
|||||||||||||||
плоскости |
|
||||||||||||||||||
треугольника левее линии пересечения a видна, а правее - не видна.

|
|
|
30 |
|
|
|
|
|
à) |
B7 |
E6 |
|
á) |
|
|
|
|
|
6 |
|
|
|
M7 |
|
||
|
|
|
|
|
|
|
||
|
|
5 |
|
|
|
|
|
|
N6 |
M4 |
4 |
|
|
|
|
|
a |
D3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
A6 |
F4 |
0 |
2 |
4ì |
|
|
|
|
|
a |
|
|
|
N |
|||
|
|
|
|
|
|
|
||
|
|
nà |
Рис. 13.4 |
|
|
|
nià |
|
|
|
i |
|
|
|
|
||
На рис. 13.4,б построена линия a пересечения плоскостей , |
||||||||
заданной масштабом уклона n i |
, и Ã, заданной проекцией h7Ã гори- |
|||||||
зонтали, |
уклоном |
ià =1:2 и его направлением. |
После построения |
|||||
масштаба уклона n |
à плоскости à (nà |
h Ã, l |
à |
=2 ì) |
линию пересече- |
|||
|
|
i |
i |
7 |
|
h 7Ã |
и N=h10 h10Ã . |
|
ния a плоскостей проводят через точки M=h 7 |
||||||||
Плоскости с параллельными масштабами уклона пересекают- |
||||||||
ся по горизонтали. Так, на рис. 13.5,а |
плоскости |
и Ã пересекают- |
||||||
ся по горизонтали с отметкой 6,2. Проекция горизонтали проходит через точку пересечения прямых линий, соединяющих две пары проекций точек с одинаковыми отметками, но расположенных на линиях ската разных плоскостей. Отметка 6,2 линии пересечения
определена приближенно. |
|
A9 |
|
|
9 |
||
à) nÃi |
|
|
á) |
|
|
|
8 |
5 |
ni |
|
B8 |
|
|
||
8 |
|
p |
C7 |
|
|
7 |
|
|
|
|
|
|
|||
7 |
6 |
h |
ni |
|
|
|
|
|
|
|
|
|
|
||
6 |
|
6,2 |
|
|
|
|
6 |
|
|
D6 |
|
|
|
||
5 |
|
|
|
|
|
||
7 |
|
|
E5 |
|
|
5 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
4 |
0 1 |
2 |
3ì |
|
F4 |
|
|
|
|
|
|
|
0 |
1 |
2 |
3ì |
Рис. 13.5
