
fel10E060
.pdf
11
строят профили (A,B) и (D,E) заданных прямых, а на них - профильные проекции M и N точек M и N:
|
M |
(A,B) |
(M ,M) |
(A1,B2) |
|
N |
(D,E) |
(N ,N) |
(D-2,E4) |
|
A1 |
|
E |
|
|
|
N |
|
|
|
|
|
|
|
A |
|
|
HN |
E4 |
|
|
|
|
|
|
|
|
|
N M |
D-2 |
|
|
HM |
|
|
|
|
M |
B2 |
|
D |
|
|
B |
|
-1 0 1 2 3ì |
|
||
|
|
Рис. 11.16 |
|
|
|
|
|
|
a |
|
|
9 |
10 |
|
|
|
|
b |
|
|
|
8 |
|
|
7 |
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
d |
0 1 |
2 3 4 5ì |
|
6 |
|
|
|
|||
|
|
Рис. 11.17 |
|
|
M = (M ,M)
,M) 
 (A,B);
(A,B);
N = (N ,N)
,N)  (D,E).
(D,E).
По проекциям M и N определяют отметки точек
M и N. HM = M
M ,M
,M 
 1,7ì ;
1,7ì ;
HN =  N
N ,N
,N 
 3ì в соответствии с линейным масштабом. H M = HN, поэтому прямые скрещиваются.
3ì в соответствии с линейным масштабом. H M = HN, поэтому прямые скрещиваются.
Параллельные прямые имеют параллельные проекции, одинаковое направление уменьшения отметок и один и тот же интервал (уклон).
На рис. 11.17 прямые a и d параллельны (параллельны их проекции, направления спуска совпадают и la=ld=3ì), а прямая b скрещивается с ними (lb=2 ì).
11.5. Задание кривых линий
В общем случае кривые в проекциях с числовыми отметками представляются их проекциями, являющимися кривыми линиями, и проекциями некоторого числа точек кривой с указанными числовыми отметками. Так, на рис. 11.18 своей проекцией k и расположенными на ней проекциями точек с отметками 1, 2, 3, 2, 2, 3, 4, 5 представлена кривая k. Эти точки градуируют k, деля её на дуги

|
|
|
|
|
|
12 |
|
|
|
|
M |
C |
HM |
|
с превышением каждой, |
||
|
|
|
Q5 |
равным 1 м. Интервалы кри- |
||||
|
B |
|
|
|
вой различны, |
различен |
и |
|
|
|
|
k |
|
||||
|
|
M |
|
|
уклон кривой в |
разных |
её |
|
|
|
|
|
|
||||
|
B2 |
|
C3 |
E2 |
G4 точках. |
|
|
|
|
(M ) |
F3 |
Поясним, почему мы ут- |
|||||
|
D2 |
|||||||
A1 |
|
|
верждаем, что кривая k |
на |
||||
|
0 1 2 |
3 4ì |
|
|||||
|
|
чертеже (рис. 11.18) представ- |
||||||
|
|
|
Рис. 11.18 |
|
лена, а не задана. Для этого на |
|||
|
|
|
|
проекции k возьмём проекцию |
||||
M |
произвольной точки M |
k и попробуем определить её отметку: |
||||||
если это можно сделать однозначно, то кривая k на чертеже задана. Однако оказывается, что по проекции точки M  k нельзя точно указать её отметку, а можно только констатировать, что на градуированной кривой отметка HM точки M лежит в пределах от 2 м до 3 м. Вывод: кривая на чертеже не задана, а лишь представлена проекцией и дискретным рядом градуирующих её точек.
k нельзя точно указать её отметку, а можно только констатировать, что на градуированной кривой отметка HM точки M лежит в пределах от 2 м до 3 м. Вывод: кривая на чертеже не задана, а лишь представлена проекцией и дискретным рядом градуирующих её точек.
Для приближенного определения числовой отметки точки M используем следующий способ. Дугу кривой с точкой M, ограниченную точками B и C, аппроксимируем отрезком прямой [B,C], считая, что M (M
(M )
)  [B2,C3]. Построив профиль отрезка [B,C] и определив
[B2,C3]. Построив профиль отрезка [B,C] и определив
на нем положение точки M = |
(M ,M) [B,C], где (M ,M) |
[B2 ,C3 ], |
найдем отметку точки M: H M |
2,3 ì . |
|
3 |
В частном случае, когда |
|
плоская кривая лежит в плос- |
||
|
||
|
кости уровня, параллельной |
|
|
Ï , она является горизонталью |
4и как горизонтальная прямая задается в проекциях с число-
0 1 2 3 4ì |
выми отметками своей проек- |
|
цией и числовой отметкой, |
Рис. 11.19 |
соответствующей высотам |
всех точек кривой (рис. 11.19). |

13
Л Е К Ц И Я 12
ЗАДАНИЕ ПОВЕРХНОСТЕЙ
12.1. Задание плоскости
Как и на комплексном чертеже плоскость общего положения в проекциях с числовыми отметками может быть задана тремя точками, двумя параллельными прямыми, двумя пересекающимися прямыми, прямой и точкой, любым плоским отсеком. Но при решении позиционных и метрических задач возникает необходимость в градуировании плоскости и задании её масштабом уклона или горизонталями.
ПРИМЕР 12.1. Треугольным отсеком задана плоскость  (A,B,C,A) (рис. 12.1). Проградуировать плоскость, построить масштаб уклона плоскости, найти её интервал, уклон и угол наклона к
(A,B,C,A) (рис. 12.1). Проградуировать плоскость, построить масштаб уклона плоскости, найти её интервал, уклон и угол наклона к
плоскости проекций.
|
7 |
|
ni |
|
|
1. |
Градуирование |
|
|
|
|
|
плоскости |
- построение её |
|||
|
|
|
|
|
|
|||
|
|
|
|
|
C7 7 горизонталей с отметками, |
|||
|
|
|
|
|
|
выраженными |
целыми |
|
|
|
|
|
|
6 |
числами и отличающимися |
||
A4 |
|
|
|
|
друг от друга на единицу |
|||
|
|
|
|
|
||||
|
|
|
|
5 |
|
длины (1 м). |
|
|
|
|
|
|
|
Для |
градуирования |
||
|
|
|
|
|
|
|||
|
|
4 |
|
|
плоскости |
градуируют сто- |
||
|
|
|
|
рону треугольника, разность |
||||
|
|
|
|
|
|
|||
|
|
3 |
|
|
|
отметок |
концов |
которой |
|
|
2 |
|
|
|
наибольшая (сторона BC). |
||
|
|
|
|
|
Затем через проекцию вер- |
|||
0 |
2 |
4ì B2 2 |
|
|
|
шины треугольника, проти- |
||
|
|
Рис. 12.1 |
|
|
|
воположной градуированной |
||
|
|
|
|
|
стороне (A4 ), и |
проекцию |
||
точки на градуированной стороне с отметкой 4 проводят проекцию h4 горизонтали плоскости. Проекции других её горизонталей проходят параллельно h4 через соответствующие проекции точек градуированной стороны (B2 2, 3, 5, 6, C7
2, 3, 5, 6, C7 7).
7).
При градуировании отрезок [B2,C7] делили на 5 равных частей ( H=5ì) по способу, приведенному на рис. 11.11 (различие - на рис. 12.1 показаны лишь две прямые, делящие [B2,C7] на равные части).
H=5ì) по способу, приведенному на рис. 11.11 (различие - на рис. 12.1 показаны лишь две прямые, делящие [B2,C7] на равные части).

14
2. Масштаб уклона (падения) плоскости - градуированная проекция линии ската плоскости, которую изображают двумя параллельными прямыми (тонкой и толстой) и обозначают ni , что означает: линия ската n плоскости  определяет её уклон (напоминание: линия ската плоскости - прямая плоскости, перпендикулярная к горизонтали плоскости; по теореме о проецировании прямого угла проекции линии ската и горизонталей плоскости взаимно перпендикулярны, так как горизонтали параллельны плоскости проекций Ï
определяет её уклон (напоминание: линия ската плоскости - прямая плоскости, перпендикулярная к горизонтали плоскости; по теореме о проецировании прямого угла проекции линии ската и горизонталей плоскости взаимно перпендикулярны, так как горизонтали параллельны плоскости проекций Ï ). Через точку B2 на рис. 12.1 проведена проекция линии ската плоскости
). Через точку B2 на рис. 12.1 проведена проекция линии ската плоскости  . Её горизонтали градуируют проекцию линии ската, которая поэтому является масштабом уклона плоскости n i (ni
. Её горизонтали градуируют проекцию линии ската, которая поэтому является масштабом уклона плоскости n i (ni  h4).
h4).
3.Угол наклона плоскости к плоскости проекций определяется углом  наклона к ней линии ската плоскости. Для нахождения угла
наклона к ней линии ската плоскости. Для нахождения угла  можно построить профиль какого-то отрезка линии ската (на рис.
можно построить профиль какого-то отрезка линии ската (на рис.
12.1построен профиль [2,7] отрезка [2,7] линии ската плоскости  ).
).
4.Интервал плоскости - расстояние между соседними проекциями её горизонталей с отметками, отличающимися на единицу длины. Поэтому интервал наклона плоскости равен интервалу её
линии ската. На рис. 12.1 обозначен интервал l плоскости
плоскости  .
.
Уклон i |
плоскости определяется уклоном её линии ската. |
|
Уклон i можно подсчитать по одной из формул: i=tg |
или i=1/l. |
|
Плоскость |
имеет спуск (уклон) в направлении |
линии ската |
плоскости от горизонталей с большими отметками к горизонталям с |
||||||
меньшими отметками. |
Масштаб уклона определяет поло- |
|||||
|
|
|
||||
|
9 |
|
жение плоскости в пространстве. |
|||
|
10 |
Следовательно, плоскость |
на чертеже |
|||
|
ni |
может быть задана масштабом уклона |
||||
|
11 |
(рис. 12.2). Такую плоскость обозначают |
||||
0 |
2 |
12 |
(n i ). |
|
уклона |
|
4ì |
Поскольку направления |
|||||
|
|
Рис. 12.2 |
(спуска) плоскости и линии ската совпа- |
|||
|
|
дают, то плоскость может быть задана |
||||
|
|
|
||||
|
|
Бергштрих |
одной своей горизонталью, уклоном |
|||
|
|
плоскости и его направлением, обозна- |
||||
|
|
|
чаемым штрихом (бергштрихом), указы- |
|||
|
h12 |
|
вающим спуск плоскости. На рис. 12.3 |
|||
0 |
2 |
4ì |
проекцией h12 горизонтали с отметкой |
|||
12, бергштрихом и уклоном |
i =1:2 |
|||||
|
|
|
||||
|
|
Рис. 12.3 |
задана плоскость (h, |
, i ). |
|
|
15 |
|
|
|
|
|
На рис. 12.4 плоскость Ã задана горизонталью 5, уклоном |
à |
||||
и его направлением. Для градуи- |
|
|
6 |
|
|
рования плоскости перпендику- |
|
|
|
|
|
лярно проекции горизонтали 5 |
|
|
5 |
à |
|
строят проекцию линии ската, |
|
5 |
|
||
|
|
|
|
||
градуируют её с интервалом lÃ= |
|
|
4 |
N |
|
=1/iÃ=3 ì, получая масштаб укло- |
|
|
|
|
|
на плоскости nÃi . Затем через |
|
|
|
|
|
точки, полученные при градуиро- |
|
|
3 |
Направление |
|
вании линии ската, параллельно |
|
|
|
простирания |
|
проекции горизонтали 5 прово- |
S |
|
nÃi |
0 2 |
4ì |
дят проекции горизонталей 6, 4, 3 |
|
Рис. 12.4 |
|
||
плоскости. |
|
|
|
||
При решении ряда инженерных задач необходимо ориентировать плоскость относительно меридиана Земли. Направлением простирания плоскости считают левое направление её горизонталей при взгляде на плоскость вдоль линии ската в сторону убывания её отметок (рис. 12.4). Угол 
 между северной стороной магнитной стрелки компаса и направлением простирания, измеренный против часовой стрелки, называется углом простирания плоскости. Угол простирания плоскости и её уклон определяют положение плоскости относительно сторон света.
между северной стороной магнитной стрелки компаса и направлением простирания, измеренный против часовой стрелки, называется углом простирания плоскости. Угол простирания плоскости и её уклон определяют положение плоскости относительно сторон света.
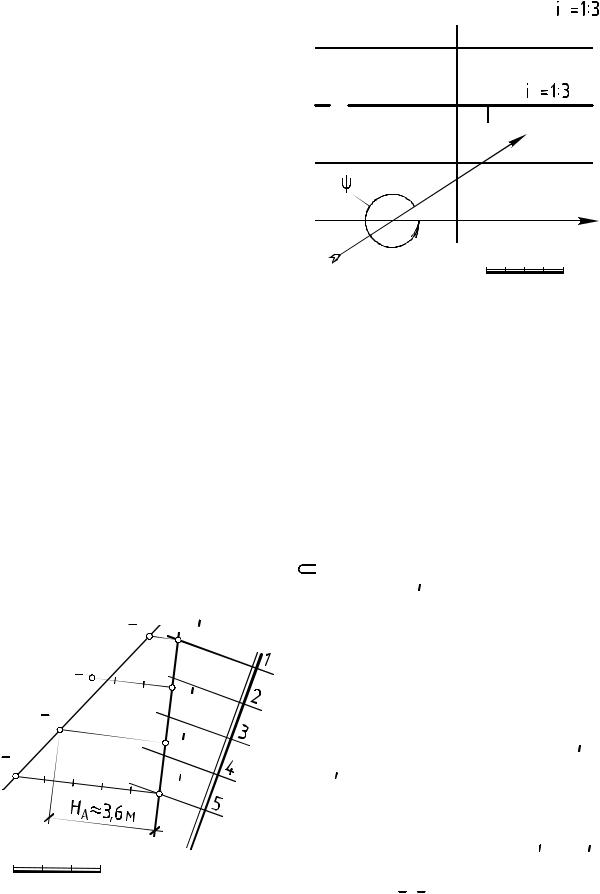
Рассмотрим задачу на принадлежность точки плоскости. ПРИМЕР 12.2. Плоскость Ã задана масштабом уклона nÃi (рис.
12.5). Определить высоту точки A |
à и проверить, принадлежит ли |
|||||
плоскости точка D, заданная своей проекцией D2,8. |
|
|||||
B |
B1 |
П р о в е д е м п р о е к ц и и |
||||
горизонталей |
плоскости через |
|||||
|
|
|||||
D |
|
точки деления масштаба уклона |
||||
D2,8 |
nÃi перпендикулярно последнему. |
|||||
A |
Точка |
принадлежит плоскости, |
||||
|
||||||
A? |
если |
она |
принадлежит прямой |
|||
|
||||||
C |
этой плоскости. Через точки D 2,8 |
|||||
|
||||||
|
C5 |
и A? проведем проекцию прямой |
||||
|
|
(B,C) плоскости Ã, пересекающую |
||||
0 1 2 3ì |
|
проекции её |
горизонталей с |
|||
nÃi |
отметками 1 и 5 в точках B1 и C5 |
|||||
Рис. 12.5 |
соответственно. Строим профиль |
|||||
прямой |
(B,C) |
и профильную |
||||
|
|
|||||

|
|
16 |
проекцию D точки |
D. Так как D |
(B,C), то D (B,C) и D Ã. |
Отметка HA 3,6 ì |
определена по точке A профиля (B,C). |
|
Две плоскости параллельны, если у них одинаковые углы простирания и уклоны. Другой признак параллельности плоскостей: две плоскости параллельны, если параллельны их горизонтали, одинаков уклон плоскостей и совпадает его направление.
12.2. Задание конической поверхности
При проектировании поверхностей искусственных земляных сооружений часто используется коническая поверхность вращения с вертикальной осью, называемая также прямой круговой конической поверхностью, прямым круговым конусом или просто конусом вращения. Эта поверхность может быть образована вращением прямой t (образующей) вокруг пересекающей её оси j и описана формулой Ô {t(t,j;t 
 j)(ti =t
j)(ti =t  j)}, где Ô - буква, обозначающая поверхность. Точка пересечения образующей и оси конической поверхности является её вершиной. Любое сечение этой поверхности плоскостью, перпендикулярной оси вращения, есть окружность.
j)}, где Ô - буква, обозначающая поверхность. Точка пересечения образующей и оси конической поверхности является её вершиной. Любое сечение этой поверхности плоскостью, перпендикулярной оси вращения, есть окружность.
Сечения поверхности горизонтальными плоскостями называют горизонталями поверхности. Горизонталями конической поверхности вращения при вертикальном положении её оси являются окружности с центрами на этой оси. На плоскость проекций они проецируются в концентрические окружности, а ось вращения и вершина поверхности - в одну точку, центр этих окружностей (рис. 12.6).
Построение горизонталей поверхности c отметками, выраженными целыми числами, отличающимися на единицу длины, называет-
ся |
градуированием поверхности. Радиусы |
проекций соседних |
|||
|
|
h0 |
горизонталей, градуирующих по- |
||
|
|
верхность |
конуса |
вращения, |
|
|
|
h1 |
отличаются на величину интервала |
||
|
|
lÔ поверхности, равного интервалу |
|||
|
|
V3 j |
l её образующей. Горизонтали, |
||
|
|
h2 |
градуирующие поверхность, гра- |
||
|
|
дуируют и все её образующие. |
|||
|
|
|
Градуированная проекция любой |
||
|
|
|
образующей является |
масштабом |
|
|
|
nÔi t |
уклона n Ôi , а сама образующая t - |
||
0 |
2 |
4ì |
линией ската поверхности. |
||
Рис. 12.6

17
На рис 12.6 показаны проекции вершины V3  j конической поверхности вращения и градуирующих её горизонталей h2 , h1 , h0, а также проградуированная проекция t какой-то образующей поверхности, являющейся масштабом уклона nÔi поверхности.
j конической поверхности вращения и градуирующих её горизонталей h2 , h1 , h0, а также проградуированная проекция t какой-то образующей поверхности, являющейся масштабом уклона nÔi поверхности.
Поверхность конуса вращения с вертикальной осью может быть задана проекцией её вершины с числовой отметкой и масштабом уклона (рис. 12.7, а), но чаще вместо масштаба уклона
à) |
á) |
|
задают уклон образующих |
|
V |
поверхности iÔ и направле- |
|||
V |
|
|||
|
6 |
|
||
6 |
|
|
ние их спуска (рис. 12.7,б). В |
|
|
|
|
||
|
|
|
этом случае для построения |
|
|
nÔi |
|
масштаба уклона поверхнос- |
|
|
|
ти через проекцию вершины |
||
0 2 4ì |
0 |
2 4ì |
проводят проекцию любой |
|
образующей и градуируют её |
||||
|
Рис. 12.7 |
|
с интервалом, соответствую- |
|
|
|
щим заданному уклону. |
12.3. Поверхность равного уклона
Пусть по кривой a перемещается вершина прямого кругового конуса с вертикальной осью, последовательно занимая положения A, B, D,... (рис.12.8,а). Поверхности Ô и 
 , огибающие образующий конус во всех его положениях, называются поверхностями равного уклона. Линия ската каждой из этих поверхностей, проведенная через любую точку направляющей a, совпадает с той образующей конуса, по которой огибающая поверхность касается конической.
, огибающие образующий конус во всех его положениях, называются поверхностями равного уклона. Линия ската каждой из этих поверхностей, проведенная через любую точку направляющей a, совпадает с той образующей конуса, по которой огибающая поверхность касается конической.
à) |
|
á) |
|
a |
h3 |
|
D |
|
|
B |
h2 |
|
h1 |
|
A |
h0 |
Ô |
|
Рис. 12.8

18
Поэтому образующей поверхности равного уклона может быть прямая линия и поверхность отнесена к линейчатым. Поверхность равного уклона - это линейчатая поверхность, образующая которой, перемещаясь по направляющей, имеет постоянный угол наклона к горизонтальной плоскости и является линией ската поверхности. Такую форму имеют, например, поверхности откосов насыпей и выемок на подъемах и спусках криволинейных участков дорог (рис. 12.8,б). Каждая горизонталь поверхности равного уклона представляет собой огибающую окружностей - горизонталей конусов, расположенных в одной горизонтальной плоскости.
На рис. 12.9 и 12.10 приведены чертежи поверхностей равного уклона с различными направляющими a, уклоном i=1:2 и его направлением в сторону от a.
На рис. 12.9, а направляющая поверхности равного уклона - пространственная кривая a с точками A, B и C на ней. Перед градуированием поверхности в эти точки помещают вершины вспомогательных круговых конусов и сначала градуируют конические поверхности. Для этого строят проекции их горизонталей - окружности, проводимые из точек A1 , B2 и C3 радиусами, кратными интервалу l=1/i=2 ì . Линии, огибающие проекции горизонталей конических поверхностей с одинаковыми отметками, являются проекциями горизонталей поверхности равного уклона. Также строят проекции горизонталей поверхности равного уклона в случае, когда направляющая кривая расположена в вертикальной плоскости.
à) á)
a |
C3 |
0 |
4 |
8ì |
|
a9 |
|
0 |
|
6 7 |
|
C |
|||
|
2 1 |
|
8 9 8 |
|
|||
|
2 |
B2 |
|
|
7 |
|
|
|
1 |
|
|
|
|
||
|
0 |
|
B |
|
|
6 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
0 |
2 4 6 ì |
|
|
|
|
|
|
|
|
A1 |
|
A |
|
|
|
Рис. 12.9

19
Если направляющая кривая лежит в горизонтальной плоскости, то она сама есть одна из горизонталей поверхности равного уклона. На рис.12.9,б направляющей поверхности является горизонтальная кривая a с отметкой 9. Проекции горизонталей поверхности строились как на рис. 12.9,а, только точки A, B и C, имеющие одинаковые отметки, брались на a произвольно.
На рис. 12.9,а и 12.9,б заданы по две поверхности равного уклона, расположенные с разных сторон от направляющей a, по которой они пересекаются. Проекции горизонталей в обоих случаях представляют собой эквидистантные кривые: расстояния между проекциями смежных горизонталей в направлении общей нормали к ним всюду одинаковы. Когда направляющая поверхности является винтовой линией, поверхность равного уклона становится винтовой (см. раздел 12.4). Если направляющей поверхностей равного уклона служит прямая, то эти поверхности представляют собой две пересекающиеся по направляющей прямой наклонные плоскости  и Ã . Их задают проекциями горизонталей или масштабами уклона
и Ã . Их задают проекциями горизонталей или масштабами уклона
(рис. 12.10).
На рис. 12.10,а направляющая a (a7)- горизонтальная прямая, поэтому масштабы уклона плоскостей S и Ã перпендикулярны a7, а проекции их горизонталей параллельны a7 и расположены друг от друга на расстояниях, кратных интервалу плоскостей.
à) |
|
a7 |
á) |
ni |
|
|
|
|
|
|
7 |
|
4 5 6 |
6 5 4 nÃi |
|
a |
|
ni |
|
|
6 |
||
|
|
|
|
5 |
nÃi |
|
0 |
2 4 6ì |
4 |
0 1 |
2 3 4ì |
|
|
|
|
|
Рис. 12.10
На рис. 12.10,б направляющая прямая a, проекция a которой проградуирована, занимает общее положение. Для градуирования плоскости  в точку прямой a, например, с отметкой 7 помещали вершину вспомогательного конуса и градуировали его поверхность,
в точку прямой a, например, с отметкой 7 помещали вершину вспомогательного конуса и градуировали его поверхность,

20
проводя проекции горизонталей радиусами, кратными интервалу плоскости . Чтобы построить проекцию горизонтали плоскости  с отметкой 6, из проекции точки направляющей a с отметкой 6 проводили касательную прямую к проекции горизонтали конуса с той же отметкой. Проекции других горизонталей плоскости строились аналогично. Масштаб уклона плоскости ni перпендикулярен к проекциям её горизонталей. Градуирование плоскости Ã выполнялось несколько иначе. Сначала были построены по одной проекции горизонталей конической поверхности и плоскости Ã, имеющих одинаковую отметку, например, 6. Затем перпендикулярно проекции горизонтали плоскости строился её масштаб уклона nÃi , через точки деления которого проводились проекции других горизонталей плоскости, параллельные между собой.
с отметкой 6, из проекции точки направляющей a с отметкой 6 проводили касательную прямую к проекции горизонтали конуса с той же отметкой. Проекции других горизонталей плоскости строились аналогично. Масштаб уклона плоскости ni перпендикулярен к проекциям её горизонталей. Градуирование плоскости Ã выполнялось несколько иначе. Сначала были построены по одной проекции горизонталей конической поверхности и плоскости Ã, имеющих одинаковую отметку, например, 6. Затем перпендикулярно проекции горизонтали плоскости строился её масштаб уклона nÃi , через точки деления которого проводились проекции других горизонталей плоскости, параллельные между собой.
12.4. Винтовые поверхности
На рис. 12.11 дано наглядное изображение съезда с путепровода, являющегося элементом транспортной развязки на пересечении двух автодорог, проложенных в разных уровнях. При отсутствии поперечного уклона дорожного полотна съезд ограничен поверхностью Ô прямого закрытого геликоида, а откосы насыпи - поверхностью  косого открытого геликоида. Эти винтовые поверхности наиболее часто используются при проектировании инженерных земляных сооружений.
косого открытого геликоида. Эти винтовые поверхности наиболее часто используются при проектировании инженерных земляных сооружений.
j |
|
k |
Ô |
b ti
li
a |
Эвольвента |
Рис. 12.11
