
460. Колебания и волны
.pdf
МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
КОЛЕБАНИЯ И ВОЛНЫ
Лабораторный практикум по физике
№460
МОСКВА 2009

МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ИНСТИТУТ (ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
Кафедра физики
КОЛЕБАНИЯ И ВОЛНЫ
Лабораторный практикум по физике
Под редакцией М.Я. Юшиной, Б.Л. Афанасьева, Е.А. Гусевой
МОСКВА 2009
3
Лабораторная работа № 2-К
«ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ФИЗИЧЕСКОГО МАЯТНИКА»
1.Введение
1.1.Среди механических движений важную роль играет колебательное движение, характеризующееся определённой периодичностью. Физическое описание колебаний реального тела
–чрезвычайно сложная задача. Поэтому теория колебаний оперирует с моделями: пружинным, математическим, физическим,
крутильным маятниками. В основе всех этих моделей |
лежит |
|||||||
представление о линейном гармоническом осцилляторе. |
|
|
||||||
1.2. |
В классической |
механике |
линейный |
гармонический |
||||
осциллятор – это материальная точка или абсолютно твёрдое тело, |
||||||||
совершающее |
одномерные |
гармонические |
колебания |
под |
||||
действием |
упругой (или квазиупругой) силы. |
|
|
|
||||
1.3. В настоящей лабораторной работе изучаются колебания |
||||||||
математического |
и |
физического |
маятников |
и |
определяются |
|||
параметры последнего. |
|
|
|
|
|
|
||
2. Основные понятия
2.1. Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена точечная масса. Достаточно хорошим приближением
служит небольшой тяжёлый шарик, подвешенный на |
длинной |
|||
тонкой нити. |
|
|
|
|
2.2. Отклонение |
маятника |
от |
положения |
равновесия |
определяется угловым |
смещением jr , |
образованным |
нитью с |
|
вертикалью (рис.1). При этом возникает момент силы тяжестиМ относительно оси, проходящей через точку О, равный по величине M = m g l sinφ ( m – масса маятника , l – его длина)
Вектор момента силы имеет такое направление, что стремится вернуть маятник в положение равновесия и поэтому при малых отклонениях, когда sin j » j , аналогичен квазиупругой силе. На рис.1 он направлен от нас, перпендикулярно плоскости чертежа.
Применим |
к математическому маятнику |
|
основное уравнение |
|
динамики |
r |
r |
, |
где J – момент |
&& |
|
|||
вращательного движения Jj = ‡”M |
||||
r
инерции маятника относительно упомянутой выше оси, j&& – угловое ускорение, ‡”M - сумма моментов внешних сил. Для проекций на ось вращения

4
ml |
2 |
j = - mgl sin j |
|
(1) |
|
&&& |
. |
|
|
|
|
|
|
Рис.1
При |
малых |
sin j » j |
и |
тогда |
получаем |
углах |
дифференциальное уравнение
j |
+ |
g |
|
j |
= 0 , |
(2) |
&& |
|
l |
|
|
|
|
|
|
|
|
|
|
|
решением которого являются гармонические колебания
j=j 0 cos( w0 t + a ) ,
скруговой частотой и периодом соответственно
w 0 = g |
l , |
T = 2p l g , |
(3) |
которые зависят |
только |
от длиныl маятника и |
ускорения |
свободного падения g. |
|
|
|
2.3.Физическим маятником называется твердое , тело
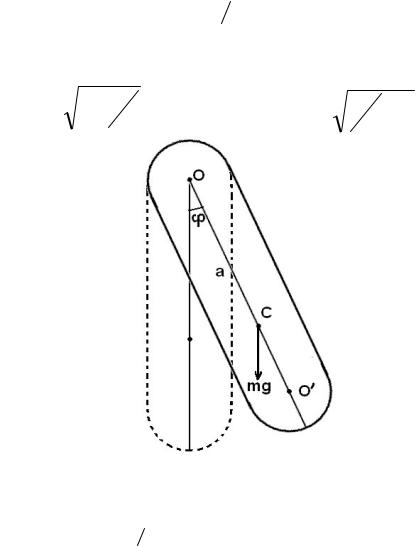
способное совершать колебания вокруг некоторой, неоси проходящей через его центр масс. В положении равновесия центр масс С находится под точкой подвесаО на одной вертикали на
расстоянии |
a |
(рис.2). При |
отклонении маятника |
от положения |
|
равновесия возникает момент силы, стремящийся |
вернуть |
его |
|||
обратно. |
|
|
|
|
|
Так же, как и для математического маятника, |
(4) |
||||
|
|
Jj = -mgl sin j . |
|||
|
|
&& |
|
|
|
Здесь |
J |
– момент |
инерции маятника относительно |
,оси |
|
проходящей через точку О. |
При малых колебаниях уравнение(4) |
||||
переходит в |
|
|
|
|
|
5
|
j + mga j J |
= 0 , |
|
(5) |
|
|
&& |
|
|
|
|
решением |
которого |
является |
j = j0 cos(w0t +a) , |
но теперь с |
|
круговой частотой |
|
|
|
|
|
w0 = |
mga |
и периодом T = 2p |
J |
|
|
J |
mga . |
(6) |
|||
|
|
Рис.2 |
|
2.4. При |
сравнении |
формул(3) и (6) видно, |
что |
математический маятник с длиной |
|
(7) |
|
lпр = J ma |
|
||
будет иметь такой же период, как и физический. Величина |
l пр |
||
называется приведённой длиной физического маятника. |
|
||
3. Описание лабораторной установки
3.1. Лабораторная установка (рис.3) состоит из вертикальной стойки 1, основания 2 и элементов подвеса математического и физического 3 маятников, состоящих из горизонтальной стальной калёной призмы 4 и зажима5. В качестве математического маятника применён стальной шарик6 небольшого диаметра, подвешенный на нити в точке на линии продолжения ребра призмы, на которое опирается физический маятник. Изменять длину нити можно, наматывая её часть на детали зажима.

6
Рис.3
4.Техника безопасности
4.1.Несмотря на кажущуюся простоту лабораторной работы, её выполнение следует проводить под руководством преподавателя
или лаборанта. Не допускать падения тяжёлого физического маятника.
5. Порядок измерений и обработка результатов
5.1.Внести данные измерительных приборов в табл. 1.
5.2.Туда же внести значения массы физического маятника и расстояния H между его опорами.
|
|
|
|
|
|
Таблица 1 |
|
Прибор |
|
Предел |
Цена деления |
|
Погрешность |
|
|
|
|
измерений |
|
|
|
|
|
|
|
|
|
|
|
|
|
Линейка |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Физ. маятник |
Значение |
|
Погрешность |
||||
|
|
|
|
|
|||
Масса m |
3,520 кг |
|
0.001 кг |
||||
|
|
|
|
|
|
||
Расстояние H |
0,660 м |
|
0,001 м |
|
|
||
5.3. Используя математический маятник как отвес, проверить |
|||||
центровку установки по острию 7. Если она нарушена, восстановить |
|||||
её с помощью установочных винтов под платформой. |
|
||||
5.4. Подвесить физический маятник так, чтобы круглый вырез |
|||||
на его конце |
оказался |
внизу. В этом случае расстояние между |
|||
точкой подвеса и центром масс а1 = (0,379 ± 0,001)м. |
|
||||
Вывести |
оба |
маятника |
из |
положения |
,равновесия |
одновременно |
отклонив |
их на одинаковый |
малый угол. Изменяя |
||

7
длину нити математического маятника, добейтесь синхронного качания обоих маятников.
5.5. Настройку маятников на синхронное качание провести5 раз, измеряя при этом линейкой приведенную длину физического маятника, состоящую из длины нити l0 и половины диаметра шарика D/2. Данные поместить в табл. 2.
5.6. Подвесить физический маятник так, чтобы круглый вырез на его конце оказался вверху. В этом случае расстояние между точкой подвеса и центром масс а2 = (0,281 ± 0,001)м.
Далее проделать измерения по пункту 5.5.
|
|
|
|
|
Таблица 2 |
nn |
|
|
Круглый вырез внизу |
|
|
|
|
|
|
|
|
1 |
l пр 1i |
D l пр 1 i |
D l 2 пр 1 i |
l пр 1 = ( ‡”l пр 1i ) / n = |
|
|
|
|
|
Dl 2 |
|
1 |
|
|
|
Dlсл1 =ta (n) ‡” 1i |
= |
|
|
|
n(n -1) |
||
2 |
|
|
|
|
|
|
|
Dl1 = Dlсл1 + Dlприб = |
|
|
3 |
|
|
|
|
|
|
|
lпр 1 = l пр 1 ± Dl1 = |
||
4 |
|
|
|
|
|
|
|
|||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Продолжение табл. 2. |
|
|
nn |
|
|
Круглый вырез вверху |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
l пр 2 i |
D l пр 2 i |
D l 2 пр 2 i |
|
|
l пр 2 = ( ‡”l пр 2 i ) / n = |
|||
|
|
|
|
|
|
|
|
|
Dl 2 |
|
1 |
|
|
|
|
|
|
|
Dlсл2 =ta (n) ‡” 2i |
= |
|
|
|
|
|
|
|
|
|
n(n -1) |
|
|
2 |
|
|
|
|
|
|
|
Dl2 |
= Dlсл 2 + Dlприб |
= |
3 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
lпр 2 = l пр 2 ± Dl2 = |
|||
4 |
|
|
|
|
|
|
|
|||
5 |
|
|
|
|
|
|
|
|
|
|
В |
табл. 2 |
рассчитать по |
представленным |
формулам приведённые |
||||||
длины l пр 1 , l пр 2 |
с погрешностями |
D |
l1 , |
D |
l 2 ( |
ѓС |
|
|||
|
|
0 . 9 (5) = 2,1). Далее в |
||||||||
формулах |
l 1 ЃЯl пр 1 , |
l 2 ЃЯl пр |
2 . |
|
|
|
|
|||
|
5.7. Исходя из формулы (7) рассчитать моменты инерции |
|||||||||
J1 = ma1l1 , J2 = ma2l2 .

|
|
|
|
|
8 |
|
|
|
|
|
|
|
|||
5.8. |
|
|
|
|
|
|
|
Найти |
|
|
|
|
|
|
абсолютные |
погрешности |
|
Da1 |
|
Dl1 |
|
|
|
|
Da2 |
|
Dl2 |
|
|||
DJ1 |
= ( |
Dm |
+ |
+ |
)J1 , DJ 2 |
= ( |
Dm |
+ |
+ |
)J 2 . |
|||||
m |
|
|
m |
|
|
||||||||||
|
|
|
a1 |
|
|
l1 |
|
|
a2 |
l2 |
|||||
5.9. |
Представить окончательные результаты расчета в виде |
||||||||||||||
|
|||||||||||||||
|
|
|
|
|
J1 ± DJ1 = |
|
J 2 ± DJ 2 = |
. |
|||||||
Литература
1. Савельев, И. В. Курс общей физики. T.1. Механика / И. В. Савельев. - М.: Изд-во «Астрель», 2005.
Приложение
Данные H, a1, a2 являются избыточными. Покажем, что, зная Н и приведенные длины l 1 и l 2 физического маятника, можно
найти положение центра масс а1 , а2 и рассчитать момент инерции Jc относительно оси, проходящей через центр масс С.
Тело физического маятника в нашей лабораторной работе достаточно симметрично (рис. 4).
Рис.4 Из чертежа ясно, что центр масс находится на линии,
соединяющей точки подвеса (опоры). |
|
|
|
|
|
|
|
|||||||||
По теореме Штейнера |
|
|
|
|
|
|
|
|
(8) |
|||||||
|
|
J1 = Jc + ma²1 |
J2 = Jc + ma²2. |
|
|
|
|
|
|
|||||||
Исходя из формул (7) и (8), путём сравнительно сложных |
||||||||||||||||
расчётов, найдём |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
J1 = Jc / ma1 + a1 |
J2 = Jc / ma2 + a2 |
|||||||||
J |
1 |
- J |
2 |
= (J |
c |
+ ma 2 ) - (J |
c |
+ ma 2 ) = m(a |
- a |
2 |
)(a |
+ a |
2 |
) = |
||
|
|
|
1 |
|
2 |
1 |
|
1 |
|
|
||||||
|
|
|
|
|
|
= ma1l1 - ma2l 2 = mH (a1 - a2 ) |
|
|
|
|
,(9) |
|||||
|
|
|
|
|
|
a1l1 - a2l2 = H(a1 - a2 ) a1(l1 - H ) = a2 (l2 - H ) |
||||||||||
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|||
|
a1 |
= |
(H - l2 ) |
|
= K |
a1 = |
|
KH |
|
a2 = |
H |
|
(10) |
||
|
|
(H - l1) |
1+ K |
1+ K |
|||||||||||
|
a2 |
|
|
|
|
|
|||||||||
|
|
|
a1 = |
H (H - l |
2 ) |
|
a2 |
= |
|
H (H - l1 ) |
(11) |
||||
|
|
|
|
|
|
|
|
(H - l1 ) + (H - l 2 ) |
|||||||
|
|
|
|
|
(H - l1 ) + (H - l 2 ) |
|
|
||||||||
|
|
|
|
|
Jc |
= ma 1( l1 - a1 ) = ma 2 ( l 2 - a 2 ) . |
(12) |
||||||||
По указанию преподавателя выполнить расчёты по |
|||||||||||||||
формуле (11) |
и сравнить с |
|
данными |
а1, а2. Также рассчитать Jc |
|||||||||||
по формуле(12). |
|
|
|
|
|
|
|
|
|
|
|
||||
Вопросы для самоконтроля
1-й КОМПЛЕКТ
1.Дайте определение квазиупругой силы.
2.Рассчитайте приведенную длину тонкого стержня. Ось проходит через конец стержня перпендикулярно к нему.
3. Запишите |
основное |
уравнение |
динамики |
вращательного |
движения. |
|
|
|
|
2-й КОМПЛЕКТ
1.Выведите дифференциальное уравнение колебаний математического маятника.
2.Что называется приведённой длиной физического маятника?
3.Дайте определение фазы гармонического колебания.
3-й КОМПЛЕКТ
1.Приведите параметры гармонических колебаний. Чем они определяются?
2.Что представляет собой физический маятник?
3. |
Покажите |
линейную зависимость углового ускорения от |
|||
углового смещения при гармонических колебаниях маятников. |
|
||||
|
4-й КОМПЛЕКТ |
|
|
|
|
1. |
Опишите модель математического маятника. |
|
|||
2. |
Выведите |
дифференциальное |
уравнение |
колебаний |
|
физического маятника. |
|
|
|
||
3. Исходя из формулы (7) рассчитайте J через lпр. |
|
||||
|
5-й КОМПЛЕКТ |
|
|
|
|
1. |
Запишите |
решение |
дифференциального |
уравнения |
|
гармонических колебаний. |
|
|
|
||
10
2.Запишите формулы для определения периодов колебаний математического и физического маятников.
3.Дайте определение момента инерции твердого тела.
6-й КОМПЛЕКТ
1.Сформулируйте теорему Штейнера, её применение.
2.Тонкий обруч, подвешенный на гвоздь вбитый в стену,
совершает колебания в плоскости |
параллельной стене. Найти |
период малых колебаний и приведенную длину обруча. |
|
3. Покажите, что приведенная длина |
физического маятника |
lпр ≥ а. |
|
Написали описание лабораторной работы и составили вопросы для самоконтроля профессор Юшина М.Я. и ст.
преподаватель Афанасьев Б.Л.
Лабораторная работа № 3-КМ
«ИЗУЧЕНИЕ СОБСТВЕННЫХ КОЛЕБАНИЙ В ЭЛЕКТРОМАГНИТНОМ КОНТУРЕ»
1.Введение
1.1.Собственные колебания в изолированной системе происходят после окончания внешнего воздействия, которое вывело её из положения равновесия. Частота колебаний в этом случае определяется только свойствами самой системы.
1.2. В реальных колебательных системах, будь то механические или электромагнитные, процесс колебаний всегда сопровождается диссипацией (рассеянием энергии), в силу чего колебания будут затухать. В одних случаях затухание в системе стремятся сделать как можно меньше , в других - искусственно увеличивают (вводят демпфирование).
1.3.Пользуясь универсальностью законов колебаний, можно изучать поведение механической системы на аналогичной ей электромагнитной. В этом случае изменять затухание в системе очень просто – изменяя величину активного сопротивления.
1.4.Целью настоящей лабораторной работы является экспериментальное ознакомление с собственными колебаниями в
