«Определение скорости звука в воздухе»

1. Введение

1.1. Важнейшей характеристикой любой однородной среды, связанной с её упругими и инертными свойствами, является скорость распространения звуковых волн. Звуковыми обычно называют упругие волны, частоты которых лежат в диапазоне от 20 до 20000 Гц.

1.2. Прямые измерения скорости звука в воздухе (например, по времени прохождения звуковым импульсом заданного расстояния) в лабораторных условиях осуществить трудно (и шумно). В данной работе скорость звука определяется методом стоячих волн, которые образуются в столбе воздуха, заключенного внутри закрытой с обоих концов узкой, длинной трубы. В таких трубах в определенном диапазоне частот звуковые волны близки к плоским, что существенно упрощает расчеты.

2. Основные понятия

2.1.Звуковые волны в газах и жидкостях являются продольными: колебания частиц среды^ происходят вдоль направления распространения волны. Пусть в газе вдоль оси OХ распространяется плоская продольная гармоническая волна смещений

, (1)

где А - амплитуда смещений;- циклическая частота,;_V- линейная частота; _K- волновое число; ,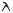- длина волны.

Рассмотрим элементарный объем газа в виде цилиндра с площадью сечения S и длиной x, его объем W = Sx. При прохождении волны (1) этот объем подвергается смещению  и деформации  (рис. 1).

Рис.1

Изменение объема газа ∆W = S приводит к изменению давления в нем на ∆P по сравнению с давлением P, которое существует в газе в отсутствие волны. В звуковой волне сжатия и расширения газа следуют друг за другом так быстро, что смежные участки среды не успевают обмениваться теплом. Такие процессы в термодинамике называются адиабатическими. В этом случае связь между давлением P и объемом W данной массы газа выражается уравнением

, (2)

где γ - показатель адиабаты, значение которого зависит от вида газа.

Логарифмируя (2) и затем дифференцируя полученное выражение, можно получить соотношение для относительных изменений давления и объема

. (3)

Дифференцируя (1) по х и подставляя в (3), получим

. (4)

Величина называется амплитудой избыточного (звукового) давления. Для обычных звуковых волн (кроме ударных) амплитуда смещений много меньше длины волны (А << λ), поэтому P₀ << P.

Таким образом, звуковая волна в газе с термодинамической точки зрения представляет собой волну избыточного давления, изменяющуюся по закону

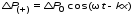, (5)

_{которая распространяется в положительном направлении оси} OХ со скоростью _.

Рис.2

На рис. 2 изображены "профили" волн избыточного давления и смещений в момент времени t = 0. Из рисунка видно, что нули смещений соответствуют максимумам (минимумам) избыточного давления.

Уравнение волны избыточного давления, распространяющейся вдоль отрицательного направления оси OX, получается заменой х на –х в (5) .

2.2. Стоячая волна образуется в результате наложения (интерференции) двух гармонических волн, распространяющихся навстречу друг другу. Уравнение стоячей волны избыточного давления (при равенстве амплитуд) имеет вид

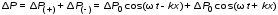
или, преобразовав,

. (6)

Из уравнения (6) следует, что в стоячей звуковой волне существуют точки, в которых избыточное давление постоянно равно нулю. Такие точки называются узлами, их координаты определяются из условия

coskx = 0 или x_уз = (m + 1/2)λ/2, (m = 0, 1, 2 ...). (7)

Точки, для которых |coskx|=1, амплитуда колебаний избыточного давления максимальна и равна 2∆P₀, называются пучностями. Координаты пучностей определяются по формуле

x_пуч = mλ/2, (m = 0, 1, 2 ...). (8)

Из (7) и (8) видно, что расстояние между двумя соседними узлами (пучностями) равно λ/2, а расстояние между соседним узлом и пучностью равноλ/4.

Рис. 3

На рис. 3 изображены "профили" стоячей волны звукового давления в различные моменты времени: сплошной линией при t = 0, пунктиром - при t = Т/2.

2.3. На практике стоячие волны чаще всего образуются при наложении прямой волны и волны, отраженной от какого-либо "препятствия".

При распространении звуковых волн в трубах такими "препятствиями" могут служить либо закрытый, либо открытый торцы трубы. Поэтому "профили" стоячих волн, которые могут возбуждаться в столбах газа в трубах, определяются условиями на торцах трубы - граничными условиями:

1) на открытом конце трубы всегда возникает узел звукового давления (так как на открытом торце труба соседствует с атмосферой) или пучность смещений (так как частицы могут свободно смещаться);

2) на закрытом конце трубы образуется пучность звукового давления (так как скачок давления возможен лишь на закрытом конце трубы) или узел смещений (так как частицы вблизи стенки не могут смещаться).

Рис. 4

На рис. 4,а показаны распределения звукового давления в закрытой с обоих концов трубе, удовлетворяющие граничным условиям (2) для первых двух видов стоячих волн-гармоник. Пунктиром дан вид распределения через полпериода. Для сравнения на рис. 4,б представлены соответствующие распределения для полузакрытой трубы (граничные условия: при х = 0 - пучность, при х = L - узел).

2.4. Частоты, соответствующие возможным при данных граничных условиях стоячим волнам, называются собственными (нормальными) частотами. Для того чтобы найти собственные частоты для закрытой трубы, сравним рис. 3 и 4,а: для первой гармоники (основной тон) - L = λ₁ / 2, для второй (первый обертон) L = 2λ₂ / 2, для третьей (второй обертон) L = 3λ₃ / 2 и т.д. В общем случае L = nλ_n / 2 , где n = 1, 2, 3, ... Отсюда

λ_n = 2 L / n. (9)

Собственные частоты соответствующих гармоник

. (10)

2.5. В лабораторной установке площади микрофона и динамика существенно меньше площади торцов трубы, поэтому ее можно считать закрытой с обоих концов (см. рис. 4, а). При возбуждении звука в закрытой трубе в ней возникают резонансы на собственных частотах, определяемых соотношением (10), причем разность частот двух соседних резонансов постоянна и равна

. (11)

Отсюда по известным иL можно найти скорость распространения звука

. (12)

2.6. Переход от одной гармоники к другой может быть также осуществлен путем изменения резонансной длины трубы L при фиксированной частоте и, следовательно, при фиксированной длине звуковой волны . Из соотношений (9), (10) и рис. 4,а следует, что изменениеd длины трубы L между двумя соседними ее резонансами равно λ/2, т.е.

. (13)

2.7. Скорость звуковых волн в газах зависит от равновесных значений давления P и температуры Т. Для идеальных газов в адиабатическом приближении теоретическое значение скорости звука можно вычислить по формуле (см. приложение)

, (14)

где γ - показатель адиабаты (γ = 1,4 для воздуха);

р, ρ - равновесные значения давления и плотности;

μ - молярная масса ; μ _возд. = 0,029 кг/моль;

R = 8,31 Дж/(мольК) - универсальная газовая постоянная;

Т - абсолютная температура.

Подставляя значения постоянных, можно получить приближенную формулу

(м/с). (15)